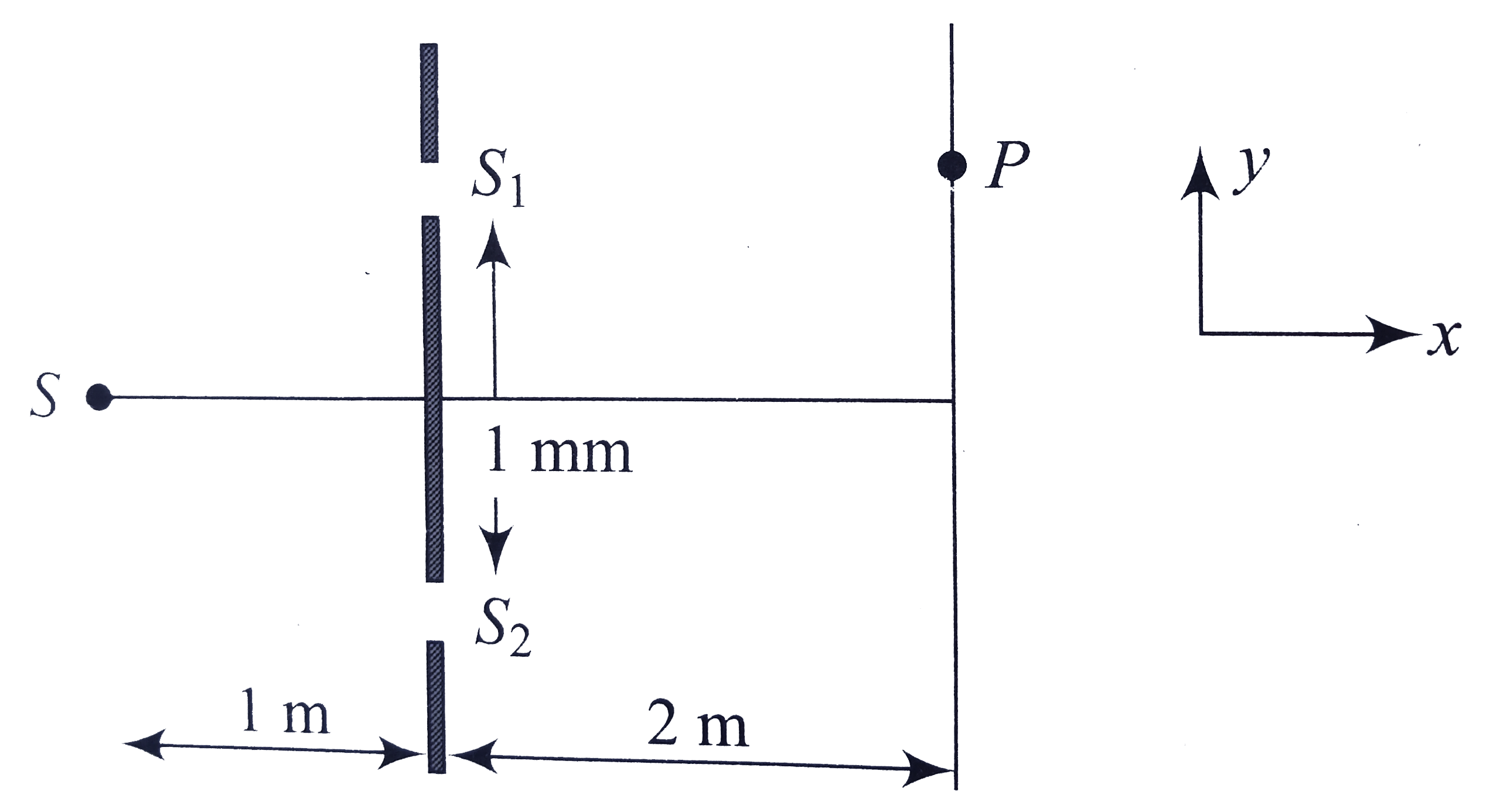
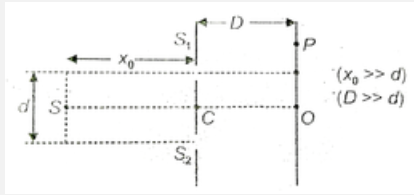
In young's double-slit experiment set up, sources S of wavelength 50 nm illumiantes two slits S1 and S2 which act as two coherent sources. The sources S oscillates about its own position according to the equation y=0.5sinπt, where y is in nm and t in seconds. The minimum value of time t for which the intensity at point P on the screen exaclty in front of the upper slit becomes minimum is
1 s
2 s
3 s
1.5 s
The correct Answer is:a
y'=d2, at point P exactly in front of S1
Δx=ydD+d22D
For minimum intensity, Δx=(2n−1)λ2(n=1)
Putting the value, we get
(0.5sinπt)×10−6+0.25×10−6=5002×10−9
0.5sinπt+0.25=0.52
sinπt=0⇒πt=0,π,2π,....
⇒t=1s
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
In the above problem, minimum value of t for which the intensity at point P on the screen exactly in front of the upper slit becomes maximum.
View SolutionIn a Young's double-slit experiment set up, source S of wavelength 6000Å illuminates two slits S1 and S2 which act two coherent sources. The sources S oscillates about its shown position according to the eqation y=1+cosπt, where y is in millimeter and t in second.
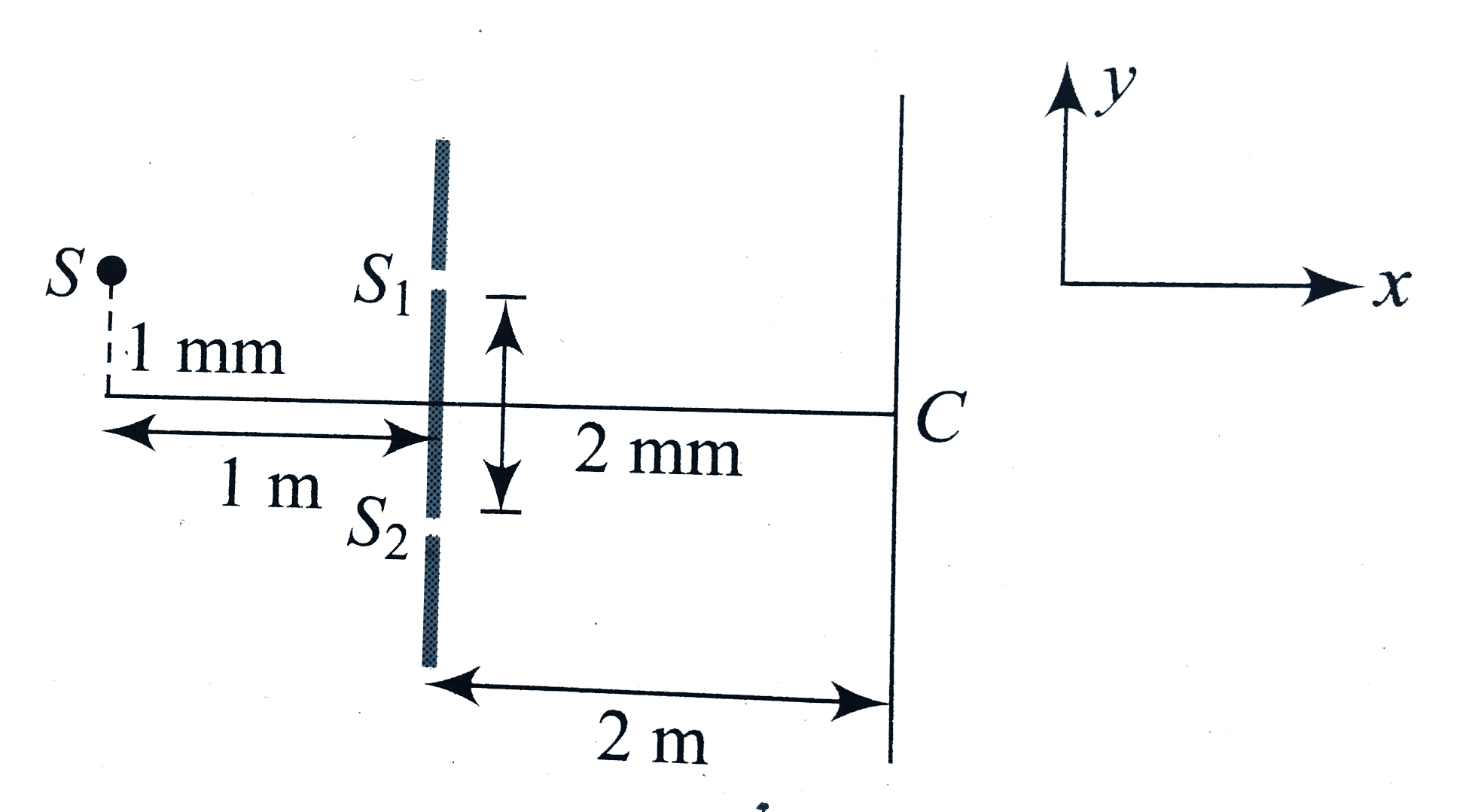
At t=2 s, the position of central maxima is
View SolutionIn a Young's double-slit experiment set up, source S of wavelength 6000Å illuminates two slits S1 and S2 which act two coherent sources. The sources S oscillates about its shown position according to the eqation y=1+cosπt, where y is in millimeter and t in second.
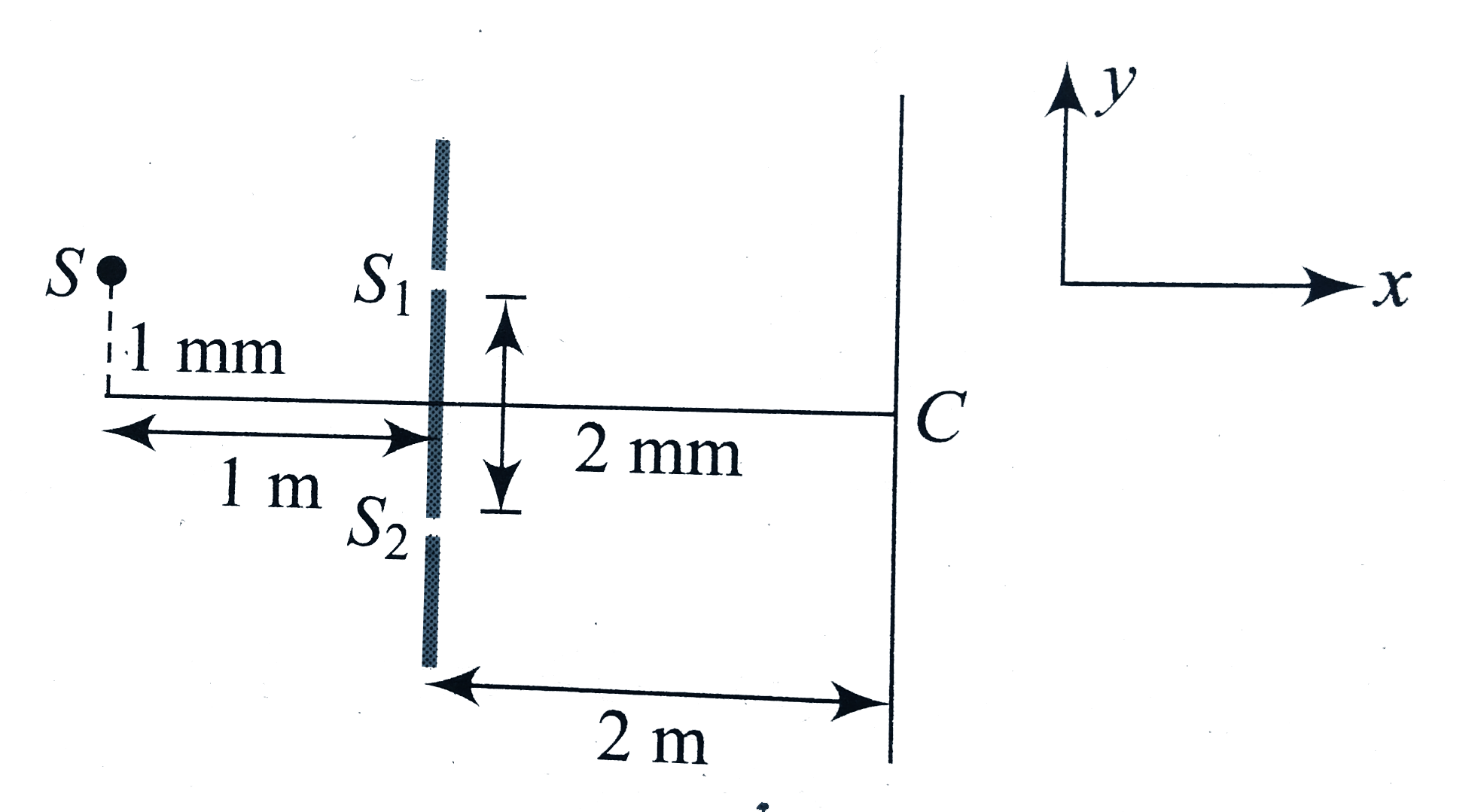
At t=0, fringe width is β1, and at t=2 s, width of figure is β2. Then
View SolutionIn Young.s double slit experiment the band width is minimum for the colour
View SolutionIn Young's double slit experiment, the ratio of maximum and minimum intensities in the fringe system is 9:1 the ratio of amplitudes of coherent sources is
View SolutionIn Young.s double slit experiment, blue-green light of wavelength 500nm is used. The slits are 1.20mm apart, and the viewing screen is 5.40m away from the slits. What is the fringe width.
View SolutionIn a Young’s double slit experiment, the source illuminating the slits is changed from blue to violet. The width of the fringes
View SolutionIn young's double slit experiment, distance between the slit S1andS2 is d and the distance between slit and screen is D . Then longest wavelength that will be missing on the screen in front of S1 is
View SolutionIn Young.s double slit experiment intensity at a point is (1/4) of the maximum intensity. Angular position of this points is
View SolutionIn a young's doule slits experiment, a monochromatic source of wavelength λ is used to illuminate the two slits
S1 and S2. The slitss S1 and S2 are identical and source S is placed symmetrically as shown. interference pattern is observed on a screen at a distance D from the centre of slit. The distance between the slits is d.
If the source is moved up by a very small distance y0, the central maxima will shift
View Solution
