In a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen.
Find the value of n.
4
6
2
8
The correct Answer is:c
To solve the problem step by step, we will follow the reasoning provided in the video transcript and break it down into clear steps.
Step 1: Understanding the Setup
In a Young's Double Slit Experiment (YDSE), we have two slits and a screen. The distance from the slits to the screen is initially given as 1.7 m. When the screen is moved 50 cm closer, the new distance from the slits to the screen becomes:
D′=1.7m−0.5m=1.2m
Step 2: Path Difference for Maximum Intensity
At point P, which is directly in front of the upper slit, the path difference is given by:
Δx=Y⋅dD
Where:
- Y is the distance from the central maximum to point P,
- d is the distance between the slits,
- D is the distance from the slits to the screen.
Since point P is at maximum intensity, we can express this as:
Δx=nλ
Where n is the order of the maximum and λ is the wavelength of the light.
Step 3: Setting Up the Equation
Given that point P lies between the third and fourth minima after moving the screen, we know that the intensity at P is one-fourth of the maximum intensity:
I=Imax4
Using the intensity formula:
I=Imaxcos2(ϕ2)
We can set up the equation:
Imax4=Imaxcos2(ϕ2)
This simplifies to:
cos2(ϕ2)=14
Thus:
cos(ϕ2)=12
This implies:
ϕ2=π3orϕ2=5π3
So:
ϕ=2π3orϕ=10π3
Step 4: Relating Phase to Path Difference
The phase difference ϕ can also be expressed in terms of the path difference:
ϕ=2πλΔx
Substituting for Δx:
ϕ=2πλ(Y⋅dD′)
Where D′=1.2m.
Step 5: Finding the Value of n
Now we can set the two expressions for ϕ equal to each other:
1. From the intensity condition:
- For ϕ=2π3:
2π3=2πλ(Y⋅d1.2)
- For ϕ=10π3:
10π3=2πλ(Y⋅d1.2)
Step 6: Solving for n
From the equations above, we can solve for n:
1. For ϕ=2π3:
Y⋅d1.2=λ3
- Rearranging gives us n=2.
2. For ϕ=10π3:
Y⋅d1.2=5λ3
- Rearranging gives us n=6.
Conclusion
The value of n that satisfies the conditions of the problem is:
n=2
In a Young's Double Slit Experiment (YDSE), we have two slits and a screen. The distance from the slits to the screen is initially given as 1.7 m. When the screen is moved 50 cm closer, the new distance from the slits to the screen becomes:
D′=1.7m−0.5m=1.2m
At point P, which is directly in front of the upper slit, the path difference is given by:
Δx=Y⋅dD
Where:
- Y is the distance from the central maximum to point P,
- d is the distance between the slits,
- D is the distance from the slits to the screen.
Δx=nλ
Where n is the order of the maximum and λ is the wavelength of the light.
Given that point P lies between the third and fourth minima after moving the screen, we know that the intensity at P is one-fourth of the maximum intensity:
I=Imax4
I=Imaxcos2(ϕ2)
We can set up the equation:
Imax4=Imaxcos2(ϕ2)
This simplifies to:
cos2(ϕ2)=14
Thus:
cos(ϕ2)=12
This implies:
ϕ2=π3orϕ2=5π3
So:
ϕ=2π3orϕ=10π3
The phase difference ϕ can also be expressed in terms of the path difference:
ϕ=2πλΔx
Substituting for Δx:
ϕ=2πλ(Y⋅dD′)
Where D′=1.2m.
Now we can set the two expressions for ϕ equal to each other:
1. From the intensity condition:
- For ϕ=2π3:
2π3=2πλ(Y⋅d1.2)
- For ϕ=10π3:
10π3=2πλ(Y⋅d1.2)
From the equations above, we can solve for n:
1. For ϕ=2π3:
Y⋅d1.2=λ3
- Rearranging gives us n=2.
Y⋅d1.2=5λ3
- Rearranging gives us n=6.
The value of n that satisfies the conditions of the problem is:
n=2
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
In a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen. ltbr> Find the wavelength of light if the separation of slits is 2 mm.
View SolutionAt a point on the screen directly in front of one of the slits, find the missing wavelengths.
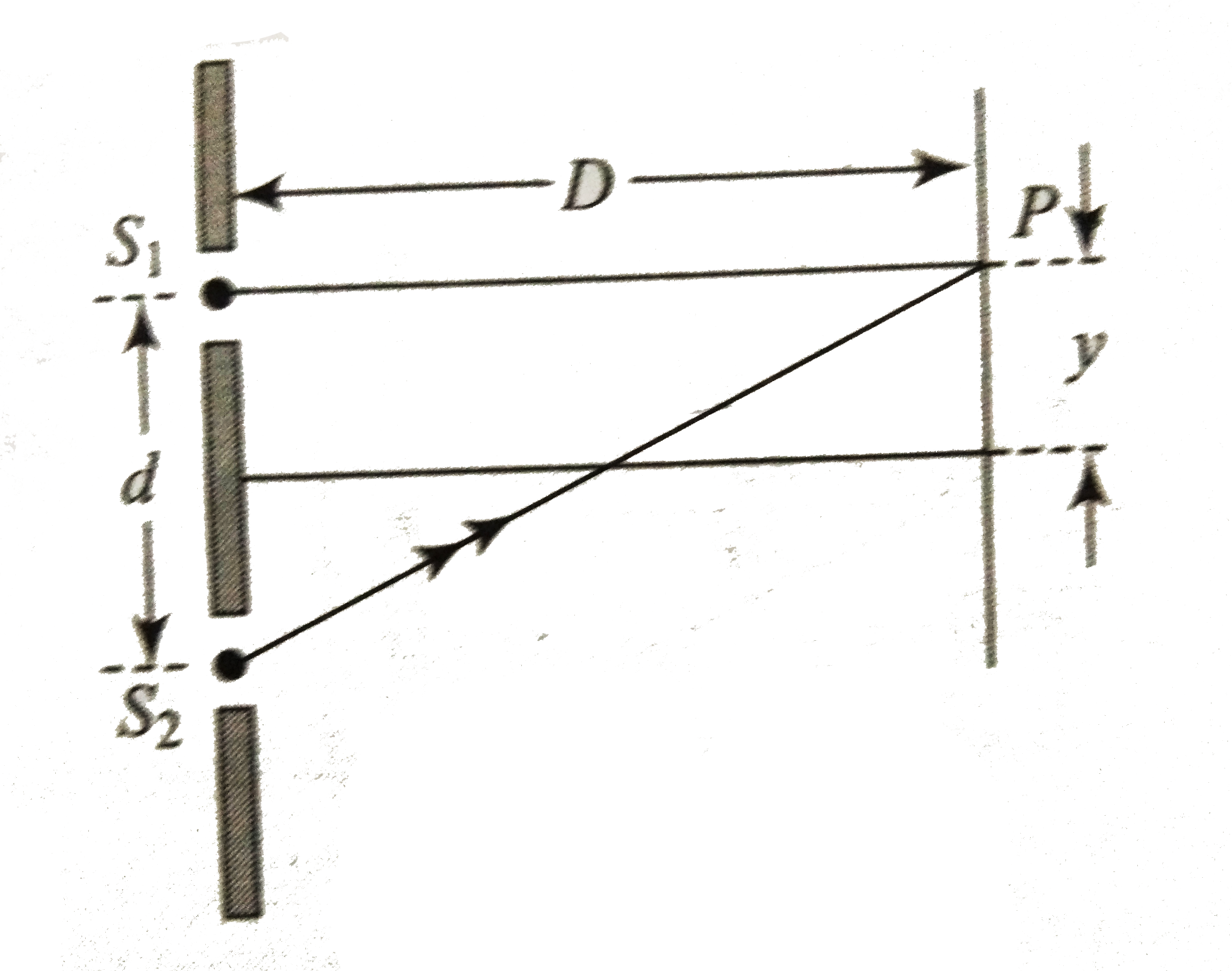
View SolutionIn the above problem, minimum value of t for which the intensity at point P on the screen exactly in front of the upper slit becomes maximum.
View SolutionIn YDSE, water is filled in the space between the slits and screen. Then
View SolutionIn YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
View SolutionIn YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
View SolutionIn Young's double-slit experment, the frist maxima is observed at a fixed point P on the screen. Now, the screen is continously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (center of the screen)

View SolutionIn Young's double-slit experment, the frist maxima is observed at a fixed point P on the screen. Now, the screen is continously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (center of the screen)

View SolutionIn a single slit diffraction method, the distance between slit and screen is 1m. The size of the slit is 0.7mm and second maximum is formed at the distance of 2mm from the centre of the screen, then find out the wavelength of light.
View SolutionIn YDSE the distance between the slits is 1mm and screen is 25nm away from intensities IF the wavelength of light is 6000A the fringe width on the screen is
View Solution
