Consider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

[3−2√2]2
[3+√2]2
[3−√2]2
[3+2√2]2
The correct Answer is:d
z=λD4d
Δx=ydD=λD4ddD=λ4
ϕ=2πλ(λ4)=π4
Intensity at S4:I4=2I0(1+cos(π2))=2I0
Intensity at S3:I3=4I0
∴ImaxImin=[(4I0)1/2+(2I0)1/2]2[(4I0)1/2−(2I0)1/2]2=⎡⎢
⎢⎣(2+√2)(2−√2)⎤⎥
⎥⎦2
=⎡⎢
⎢
⎢⎣(2+√2)24−2⎤⎥
⎥
⎥⎦2=14[4+2+4√2]2
=14[6+4√2]2=[3+2√2]2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Integer3videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Archives4videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning13videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
A glass of refractive index 1.5 is coated with a thin layer of thickness t and refractive index 1.8 Light of wavelength λ travelling in air is incident normally on the layer. It is partly reflected at the upper and the lower surfaces of the layer and two reflected rays interfere. Write the condition for their constructive interfere. If the λ=648nm, obtain the least value of t for which the rays interfere constrcutively.
06:44View SolutionA light wave of frequency 5×1014Hz enters a medium of refractive index 1.5. In the velocity of the light wave is ….. And its wavelength is ……
View SolutionStatement I: In Young's double-slit experiment, the two slits are at distance d apart. Interference pattern is observed on a screen at distance D from the slits. At a point on the screen which is directly opposite to one of the slits, a dark fringe is observed. Then, the wavelength of wave is proportional to the squar of distance between two slits.
Statement II: For a dark fringe, intensity is zero09:51View SolutionThree distinct current wires intersect a finite rectangular plane ABCD. The current is left wire and the loop is l1 . The direction of current in left most wire and righy most loop is downards as shown in the figure. The current l2through middle wire is adjusted so that the path integal of the total magnetic field along the perimeter of the rectangle is zero , that is ,∮ABCDA→B.d→s=0 then the current I2 is
 09:51View Solution
09:51View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
09:51View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d
 04:00View Solution
04:00View SolutionConsider the situation shown in fig. The two slits S_(1) and S_(2) placed symmetrically around the central line are illuminated by monochromatic light of wavelength lambda . The separation between the slit is d. The ligth transmitted by the slits falls on a screen S_(0) placed at a distance D form the slits. The slit S_(3) is at the central line and the slit S_(4) is at a distance z from S_(3) Another screen S_(c) is placed a further distance D away from S_(c) Find the ratio of the maximum to minimum intensity observed on S_(c) If z = (lambda D)/(2 d)
10:46View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
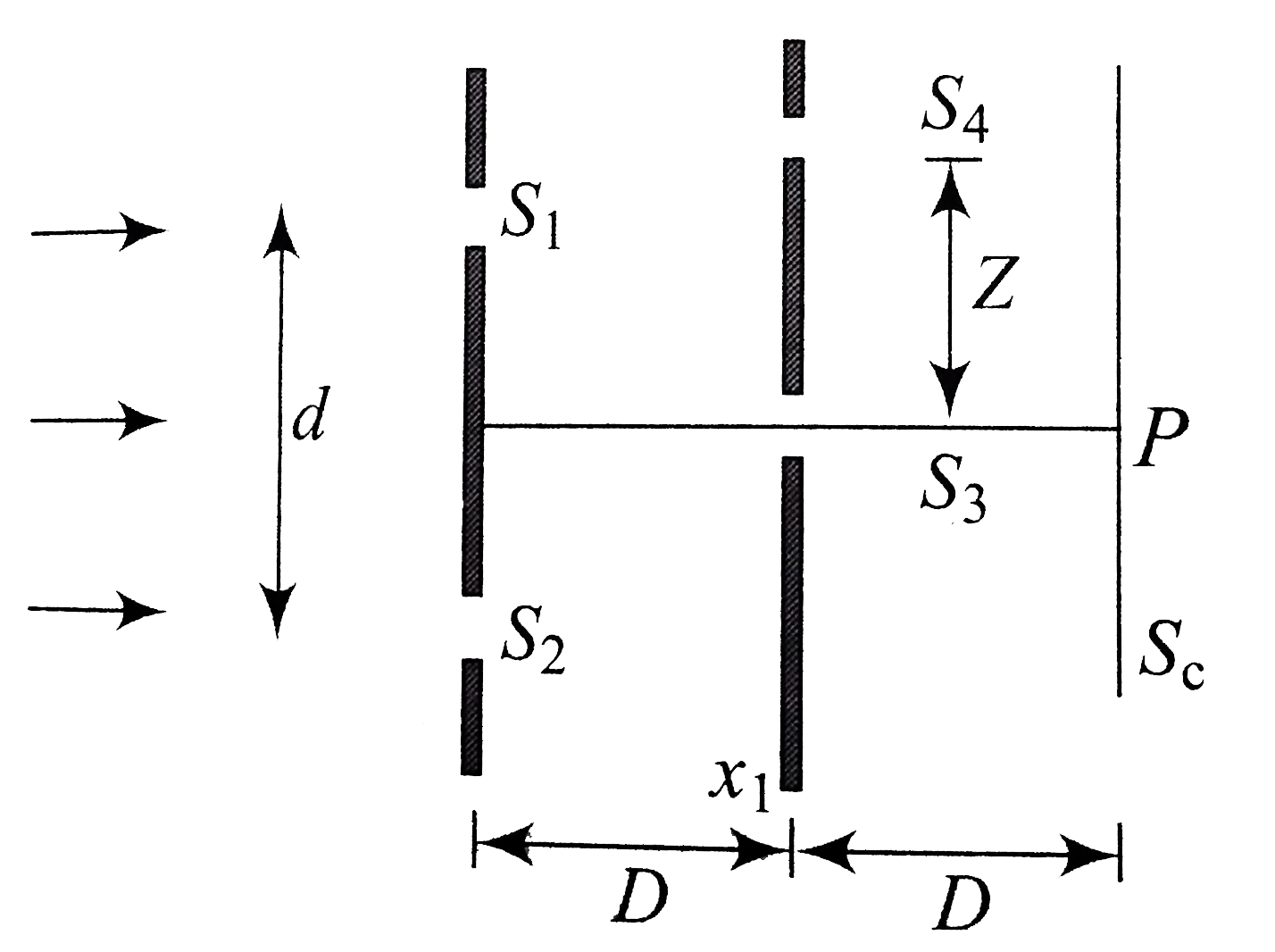
If z=λDd04:00View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
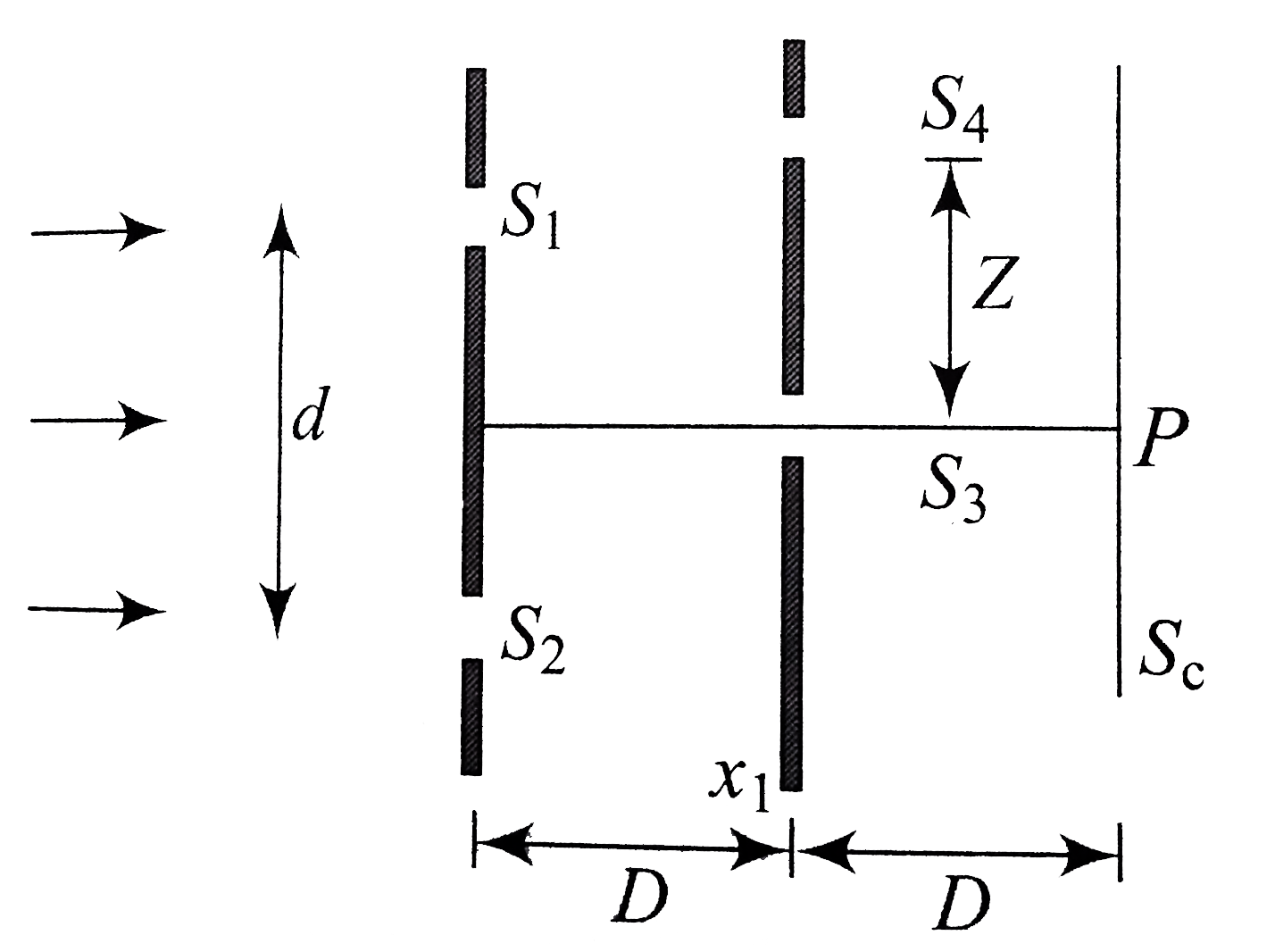
If z=λD4d02:13View SolutionIn a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is lambda and I is theintensity of central bright fringe, then intensity at distance from central maximum is
05:51View SolutionConsider the situation shown in figure-6.35. The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen E1 placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen E2 is placed a further distance D away from E1. Find the ratio of the maximum to minimum intensity observed on E2 if z is equal is : (a)λD2d (b)λDd (c)λD4d
 04:55View Solution
04:55View SolutionIn a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is λ and I is the intensity of central bright fringe, then intensity at distance from central maximum is
09:53View SolutionA light of wavelength λ falls on a narrow slit of width d.A diffraction fringe is formed on a screen placed at distance D from the slit. If the linear width of the central maximum equals to the width of the slit, will be the value of D?
View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
05:51View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d
 04:21View Solution
04:21View Solution

