Consider six wires coming into or out of the page, all with the same current. Rank the line integral of the magnetic field (from most positive to most negative) taken counterclockwise around each loop shown

B>C>D>A
B>C=D>A
B<A>C=D
C<B=D>A
The correct Answer is:C
(c) Loop B:μ0(2i−i)=∮B.dl
Loop C:μ0(i−2i)=∮B.dl
Loop A:μ0(3i−3i)=∮B.dl
Loop D:μ0(0−i)=∮B.dl
(c) B>A>C=D
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )
5 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
A square loop of wire with resistance R is moved at constant speed v across a uniform magnet field confined to a square region whose sides are twice the lengths of those of the square loop
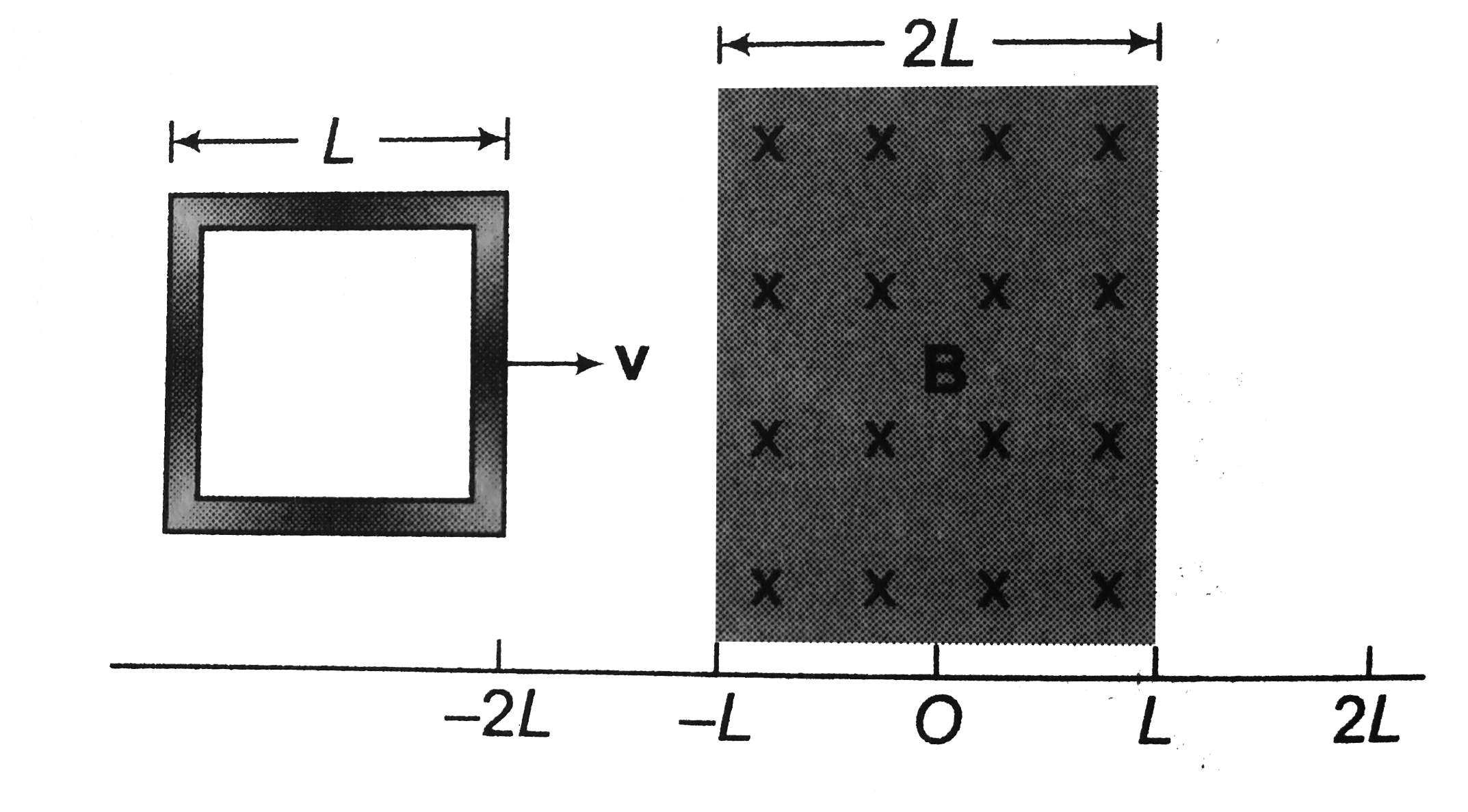
(a) Sketch a graph of the external forces F needed to move the loop at constant speed, as a function of to sketch a graph of the external force F need tho coordinate x, fromx=−2L to x=+2L. (The coordinate x is measured from the centre of the oignetic field region to the centre of the loop. It is negative when the centre of the loop is to the left, of the centre of the magnetic field region. Take positive force to be to the right). (b) Sketch a graph of the induced current in the loop as a function of x. Take counterclockwise currents to be positive.
View SolutionA current I flows along a round circular loop of radius R. Find the line integration of magnetic field along the axis of the loop from center to ∞
View SolutionConsider a circular loop of wire lying in the plane of the table. Let the current pass through the loop clockwise. Apply the right hand rule out the direction of magnetic field inside and outside the loop.
View SolutionA particle is to move along the x−axis from x=0 to x=x1 while a conservative force, directed along the x−axis, acts on the particle. For each force defination presented in the figures the maximum magnitude of the force (F1) is the same for all cases. Rank the forces according to the change in potential energy associated with the motion shown. from most positive to most negative:
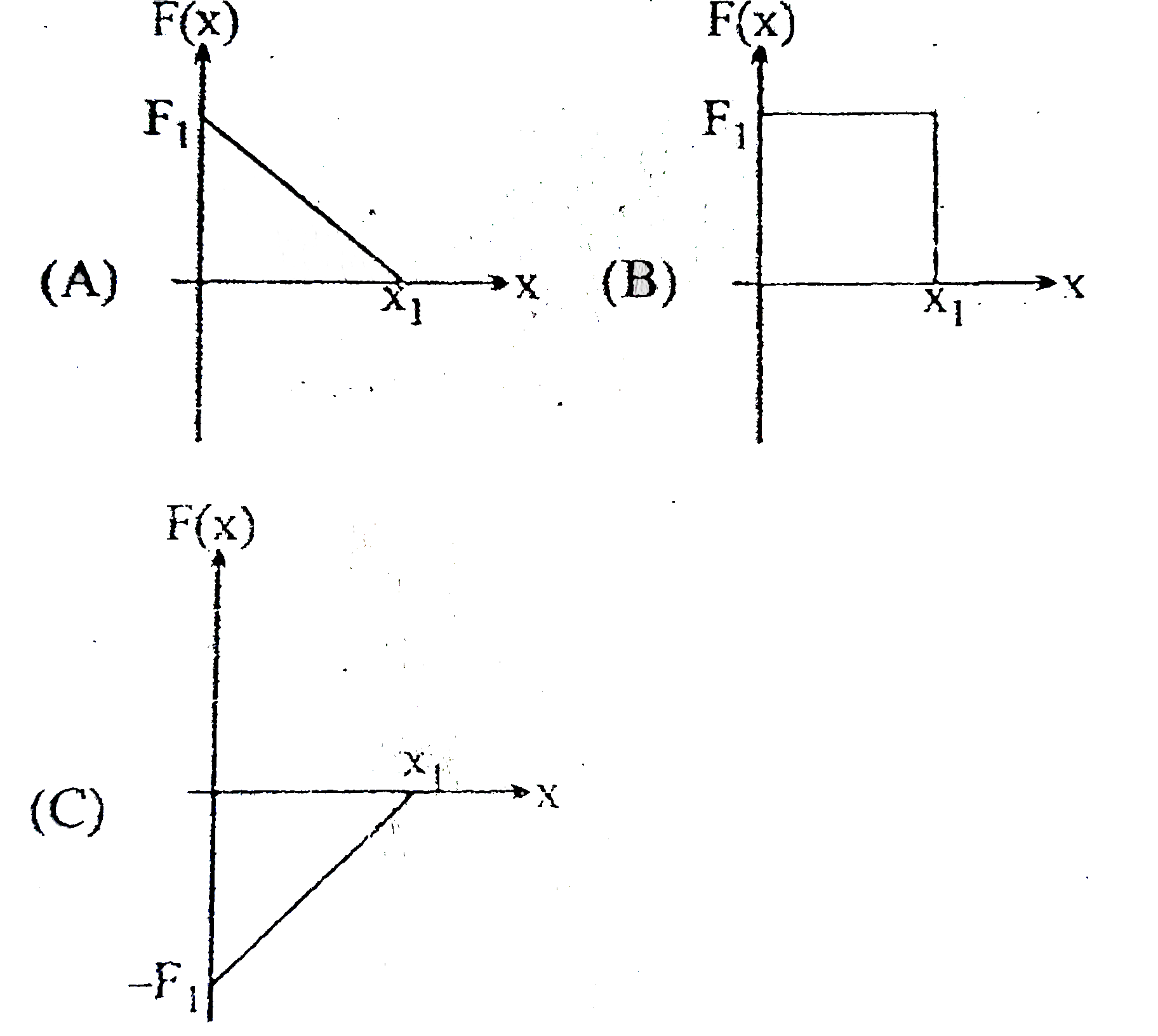
View SolutionPQRS is a square region of side 2a in the plane of paper. A uniform magnetic field B, directed perpendicular to the plane of paper and into its plane is confined within this square region. A square loop of side 'a' and made of a conducting wire of resistance R is moved at a constant velocity →v from left to right in the plane of paper as shown. Obviously, the square loop will enter the magnetic field at some time and then leave it after some time. During the motion of loop, whenever magnetic flux through it changes, emf will be induced resulting in induced current. Let the motion of the square loop be along x-axis and let us measure x coordinate of the centre of square loop from the centre of the square magnetic field region (taken as origin). Thus, x coordinate will be positive if the centre of square loop is to the right of the origin O (centre of magnetic field) and negative if centre is to the left.

External force required to maintain constant velocity of the loop for x=−95a will be
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
.
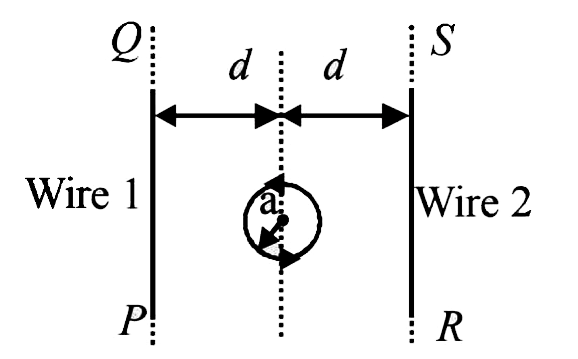
(5) Consider d>>a, and the loop is rotated about its diameter parallel to the wires by 30∘ from the position shown in the figure. If the currents in the wire are in the opposite directions, the torque on the loop at its new position will be ( assume that the net field due to the wires is constant over the loop).
View SolutionA steady current is flowing in a circular coil of radius R, made up of a thin conducting wire. The magnetic field at the centre of the loop is BL. Now, a circular loop of radius R/n is made from the same wire without changing its length, by unfounding and refolding the loop, and the same current is passed through it. If new magnetic field at the centre of the coil is BC, then the ratio BL/BC is
View SolutionA steady current is flowing in a circular coil of radius R, made up of a thin conducting wire. The magnetic field at the centre of the loop is BL. Now, a circular loop of radius R/n is made from the same wire without changing its length, by unfounding and refolding the loop, and the same current is passed through it. If new magnetic field at the centre of the coil is BC, then the ratio BL/BC is
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
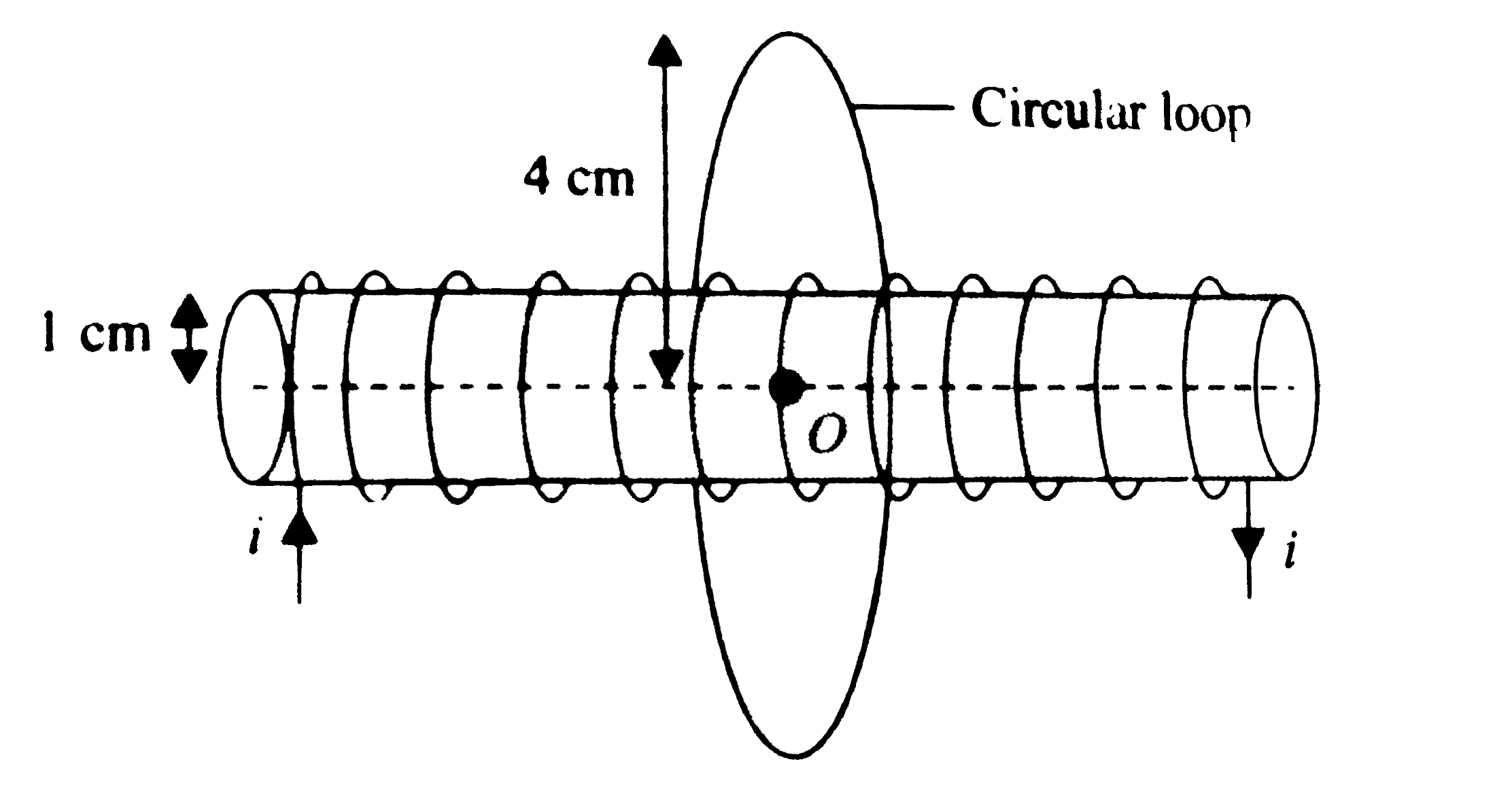
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View SolutionPQRS is a square region of side 2a in the plane of paper. A uniform magnetic field B, directed perpendicular to the plane of paper and into its plane is confined within this square region. A square loop of side 'a' and made of a conducting wire of resistance R is moved at a constant velocity →v from left to right in the plane of paper as shown. Obviously, the square loop will enter the magnetic field at some time and then leave it after some time. During the motion of loop, whenever magnetic flux through it changes, emf will be induced resulting in induced current. Let the motion of the square loop be along x-axis and let us measure x coordinate of the centre of square loop from the centre of the square magnetic field region (taken as origin). Thus, x coordinate will be positive if the centre of square loop is to the right of the origin O (centre of magnetic field) and negative if centre is to the left.

For x=a/4
(i) magnetic flux through the loop,
(ii) induced current in the loop and
(iii) external force required to maintain constant velocity of the loop, will be
View Solution
