Derive an expression for the total magnetic energy stored in two coils with inductances L1 and L2 and mutual inductance M, when the currents in the coils are I1 and I2, respectively.
To derive the expression for the total magnetic energy stored in two coils with inductances L1 and L2 and mutual inductance M, when the currents in the coils are I1 and I2, respectively, we can follow these steps:
Step 1: Define the Induced EMF in Each Coil
The induced electromotive force (EMF) in coil 1 due to its own current and the current in coil 2 can be expressed as:
E1=−L1dI1dt−MdI2dt
Similarly, the induced EMF in coil 2 is given by:
E2=−L2dI2dt−MdI1dt
Step 2: Work Done on the Charges
The work done dW in moving an elementary charge dQ in each coil can be expressed as:
dW=−E1dQ1−E2dQ2
Assuming dQ1=I1dt and dQ2=I2dt, we can substitute these into the equation:
dW=−E1I1dt−E2I2dt
Step 3: Substitute the Induced EMFs
Substituting E1 and E2 into the work done equation gives:
dW=(L1I1dI1dt+MI2dI1dt+L2I2dI2dt+MI1dI2dt)dt
Step 4: Total Work Done
To find the total work done (which is equal to the total magnetic energy stored), we integrate dW:
W=∫I10L1I1dI1+∫I20L2I2dI2+∫I10∫I20MdI1dI2
Step 5: Evaluate the Integrals
Evaluating the integrals gives:
W=12L1I21+12L2I22+MI1I2
Final Expression
Thus, the total magnetic energy U stored in the two coils is:
U=12L1I21+12L2I22+MI1I2
The induced electromotive force (EMF) in coil 1 due to its own current and the current in coil 2 can be expressed as:
E1=−L1dI1dt−MdI2dt
Similarly, the induced EMF in coil 2 is given by:
E2=−L2dI2dt−MdI1dt
The work done dW in moving an elementary charge dQ in each coil can be expressed as:
dW=−E1dQ1−E2dQ2
Assuming dQ1=I1dt and dQ2=I2dt, we can substitute these into the equation:
dW=−E1I1dt−E2I2dt
Substituting E1 and E2 into the work done equation gives:
dW=(L1I1dI1dt+MI2dI1dt+L2I2dI2dt+MI1dI2dt)dt
To find the total work done (which is equal to the total magnetic energy stored), we integrate dW:
W=∫I10L1I1dI1+∫I20L2I2dI2+∫I10∫I20MdI1dI2
Evaluating the integrals gives:
W=12L1I21+12L2I22+MI1I2
Thus, the total magnetic energy U stored in the two coils is:
U=12L1I21+12L2I22+MI1I2
Topper's Solved these Questions
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Solved Examples
Explore 3 Videos
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Exercise 4.1
Explore 24 Videos
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:HEATING EFFECT OF CURRENTExercise:Thermal Power in Resistance Connected in Circuit
Explore 27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Multiple Correct Answer type
Explore 2 Videos
Similar Questions
Knowledge Check
The mutual inductance M12 of coil 1 with respect to coil 2
Aincrease when they are brought nearer.Bdepends on the current passing through the coils.Cincreases when one of then is rotated about an axis.Dboth (a) and (b) are correct.Two different coils have self-inductances L1=8mHandL2=2mH. The current in one coil is increased at a constant rate. The current in the second coil is also increased at the same constant rate. At a certain instant of time, the power given to the two coil is the same. At that time, the current, the induced voltage and the energy stored in the first coil are i1,V1andW1 respectively. Corresponding values for the second coil at the same instant are i2,V2andW2 respectively. Then:
AW2W1=8BW2W1=18CW2W1=4DW2W1=14
Coefficient of coupling between two coils of self-inductances L1 and L2 is unity. It means
View SolutionA system consists of two coaxial current carrying circular loops as shown in Fig. The self inductance of loop 1 is L1 and self inductance of loop 2 is L2. Magnitude of mutual inductance is M. If at any instant current flowing through loop 1 and loop 2 are i1andi2 respectively, then total magnetic energy of the system is
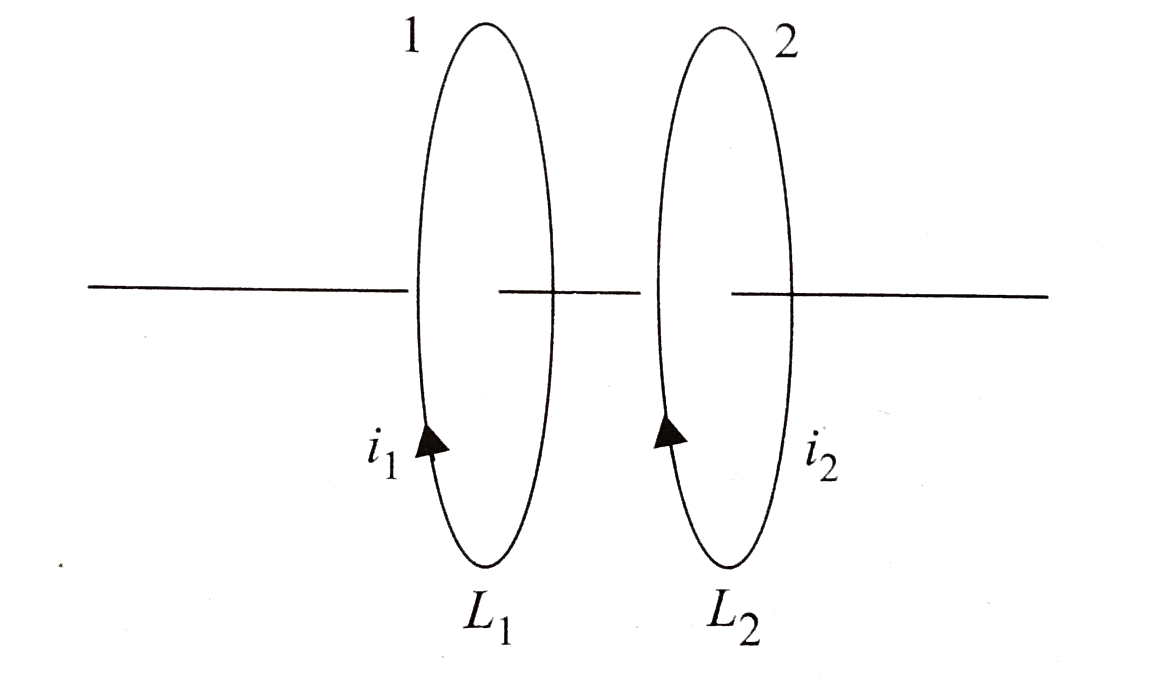
View SolutionEnergy stored in a coil of self-inductance 40mH carrying a steady current of 2 A is
View SolutionTwo different coils have self inductances L1=9mH and L2=2mH. The current in one coil is increased at a constant rate. The current in the second coil is also increased at the same constant rate. At a certain instant of time, the power given to the two coils is the same. At that time, the current the induced voltage and the energy stored in the first coil are i1,V1 and W1 respectively.
Corresponding values for the second coil at the same instant are i2,V−2 and W2 respectively. Then,
View SolutionObtain the expression for the magnetic energy stored in an ideal inductor of self inductance L when a current I passes through it.
Hence obtain the expression for the energy density of magentic field produced in the inductor.
View SolutionThe energy stored in an inductor of self inductance L carrying current l, is given by
View Solution
