Find the inductance of a unit length of two long parallel wires, each of radius a, whose centers are a distance d apart and carry equal currents in opposits directions. Neglect the flux within the wire.
μ02πIn(d−aa)
μ0πIn(d−aa)
3μ0πIn(d−aa)
μ03πIn(d−aa)
The correct Answer is:B
Since the wires are infinite, so the system of these two wires can be considered as a closed rectangle of infinite length and breadth equal to d. flux through the strip:
ϕ=∫d−aaμ0I2πr(ldr)=μ0Il2πIn(d−aa)

The other wire produces the same result, so the total flux through the dotted rectangle is
ϕ→tal=μ0lIπIn(d−aa)
The total inducatance of length l
L=ϕ→talI=μ0lπIn(d−aa)
Inductance per unit length =Ll=μ0πIn(d−aa)
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (multiple Correct )
7 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (subjective)
7 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
Calculate the self inductance per unit length of a current loop formed by joining the ends of two long parallel wires of radius r separated by a distance d between their axes, neglecting the end effects and magnetic flux within the wires.
View SolutionFigure shows an end view of two long, parallel wires perpendicular to the xy plane, each carrying a current I, but in opposite directions.

Graph the magnitude of →B at point on the x-axis.
View Solution
Knowledge Check
Find the inductance of a unit length of two parallel wires, each of radius a, whose centers are a distance d apart and carry equal currents in opposite direction. Neglect the flux within the wire.
Aμ02πIn(d−aa)Bμ0πIn(d−aa)C3μ0πIn(d−aa)D3μ03πIn(d−aa)The two linear parallel conductors carrying currents in the opposite direction…………………each other.
AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false.
Figure shows an end view of two long, parallel wires perpendicular to the xy plane, each carrying a current I, but in opposite directions.

At what value of x, the magnitude of →B is maxismum?
View SolutionForce per unit length acting at one end of each of the two long parallel wires, carrying current I each, kept distance r apart is
View SolutionIf current in two parallel wires flow in opposite directions, the force between the wires will:
View SolutionTwo thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
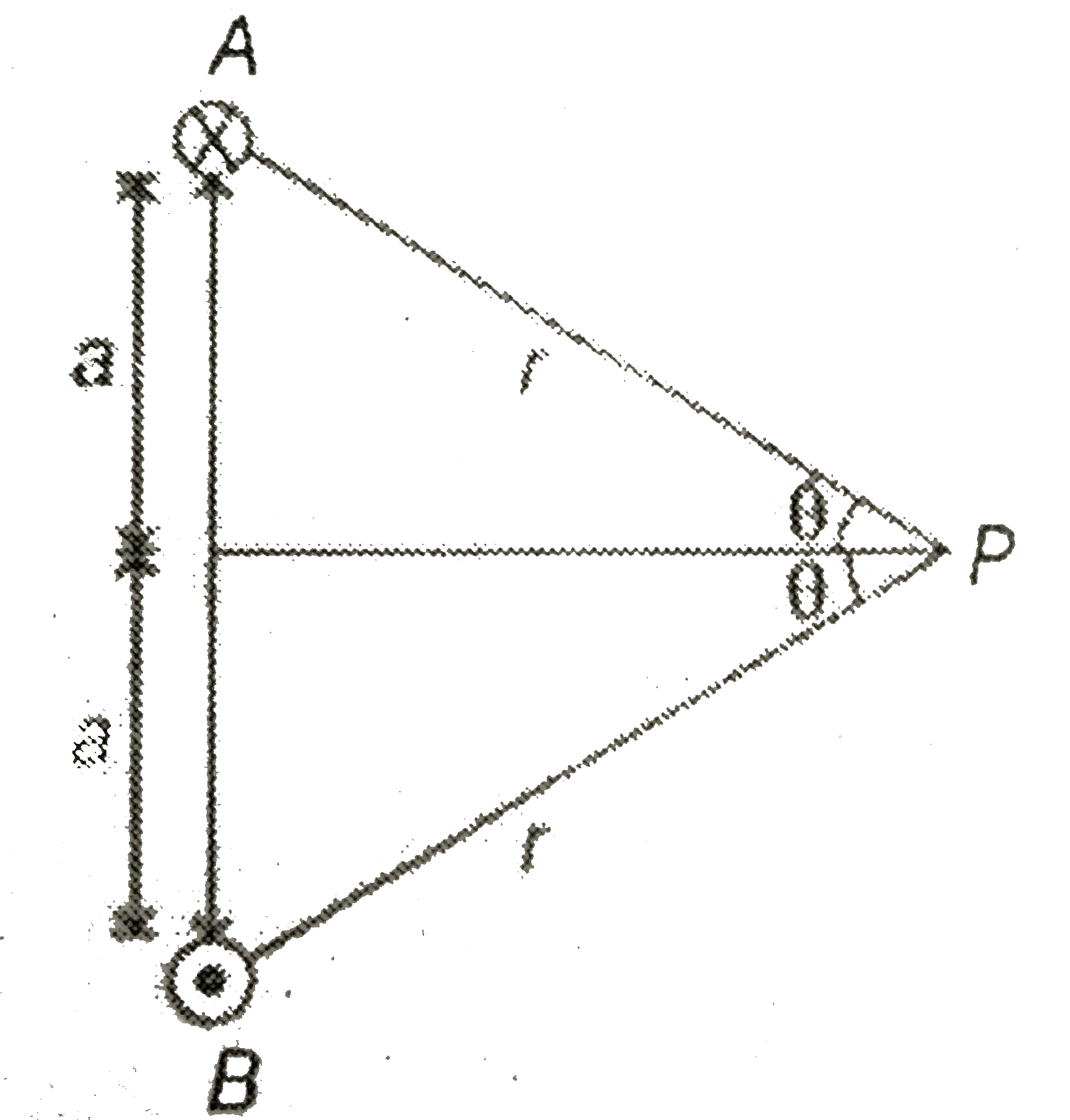
View SolutionTwo long parallel wire A and B situated perpendicuilar to the plane of the paper at a distance 2a are carrying equal currents I in opposite direction as show in the figure . The value of magnetic induction at point P situated at equal distance r from both the wires will be
View SolutionTwo long parallel wires are at a distance of 1 m. Both of them carry 1A of current. The force of attraction per unit length between the two wires is
View Solution
