An inductor and two capacitors are connected in the circuit as show in Fig Initially capacitor has no charge and capacitor has charge. Assume that the circuit has no resistance at all. At , switch is closed, then [given
and
![An inductor and two capacitors are connected in the circuit as show in Fig Initially capacitor A has no charge and capacitor B has CV charge. Assume that the circuit has no resistance at all. At t = 0, switch S is closed, then [given LC = (2)/(pi^(2) xx 10^(4)) S^(2) and Cv = 100 mC]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V05_C04_E01_098_Q01.png)
when current in the circuit is maximum, charge on each capacitor is same
when current in the circuit is maximum, charge on capacitor is twice the charge on capacitor
, where is the charge on capacitor at time
, where is the charge on capacitor at time
The correct Answer is:A, C
Let at any time, charge and current in the circuit wire are as shows.

Applying kirchoff's law,
(i)
where
At , (ii)
Differentiating (i),
At
From (ii),
From (i), (iv)
Now (v)
From (ii),
Current in the circuit is maximum for
And for , we see from (iv) and (v) that
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)2videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (linked Compreshension)36videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (single Correct )65videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
Similar Questions
Initially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.
 View Solution
View SolutionIn the circuit shown in fig. when the switch is closed, the capacitor charges with a time constant
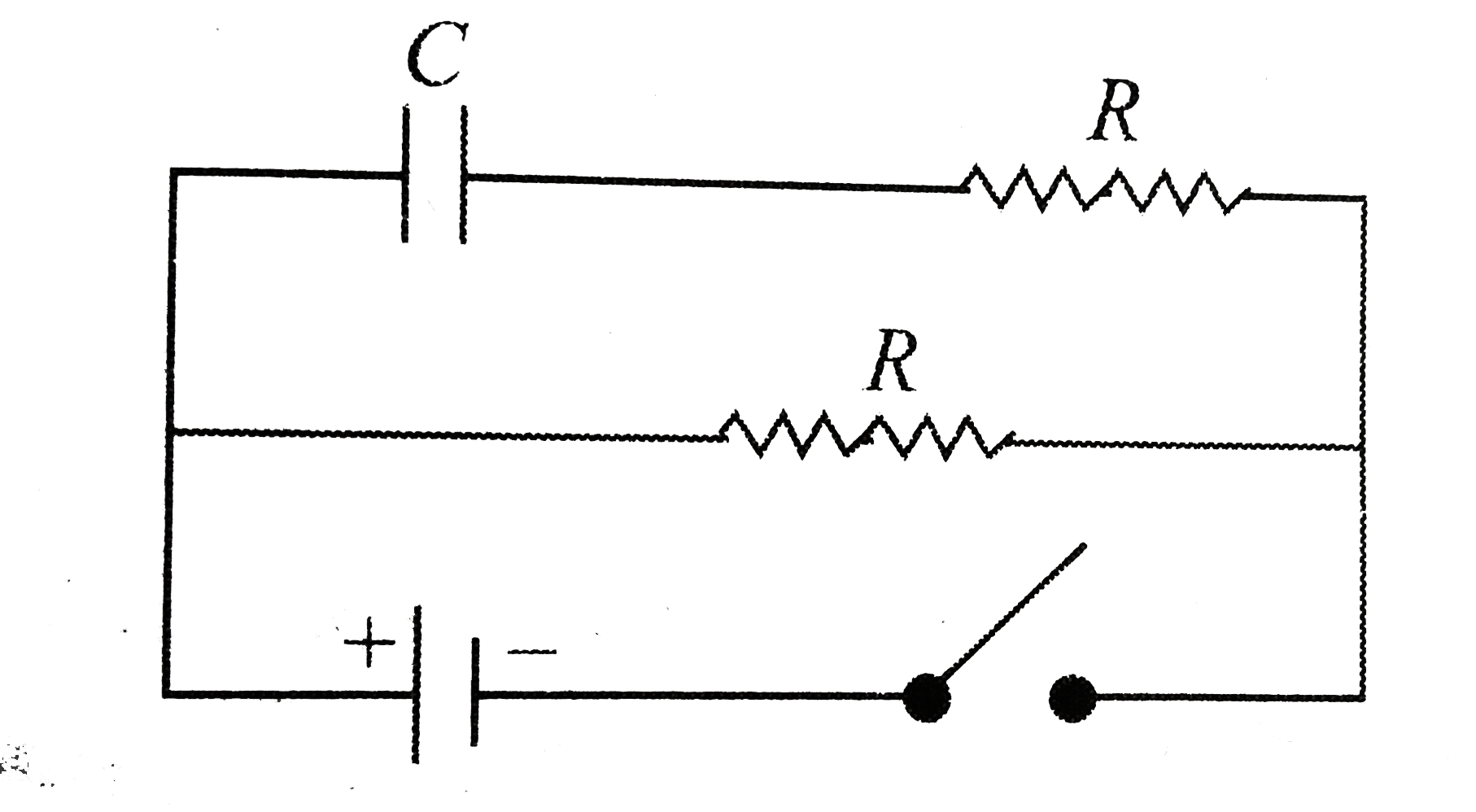 View Solution
View SolutionConisder the istuation shown in the figure. The capacitor A has a charge q on it whereas B is unchanged. The charge appearing on the capacitor B a long time after the switch is closed is
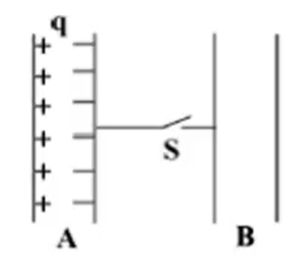 View Solution
View SolutionIn the given LC circuit,if initially capacitor C has charge Q on it and 2C has charge 2Q. The polar ar as shown in figure. Then after closing switch S and t=0
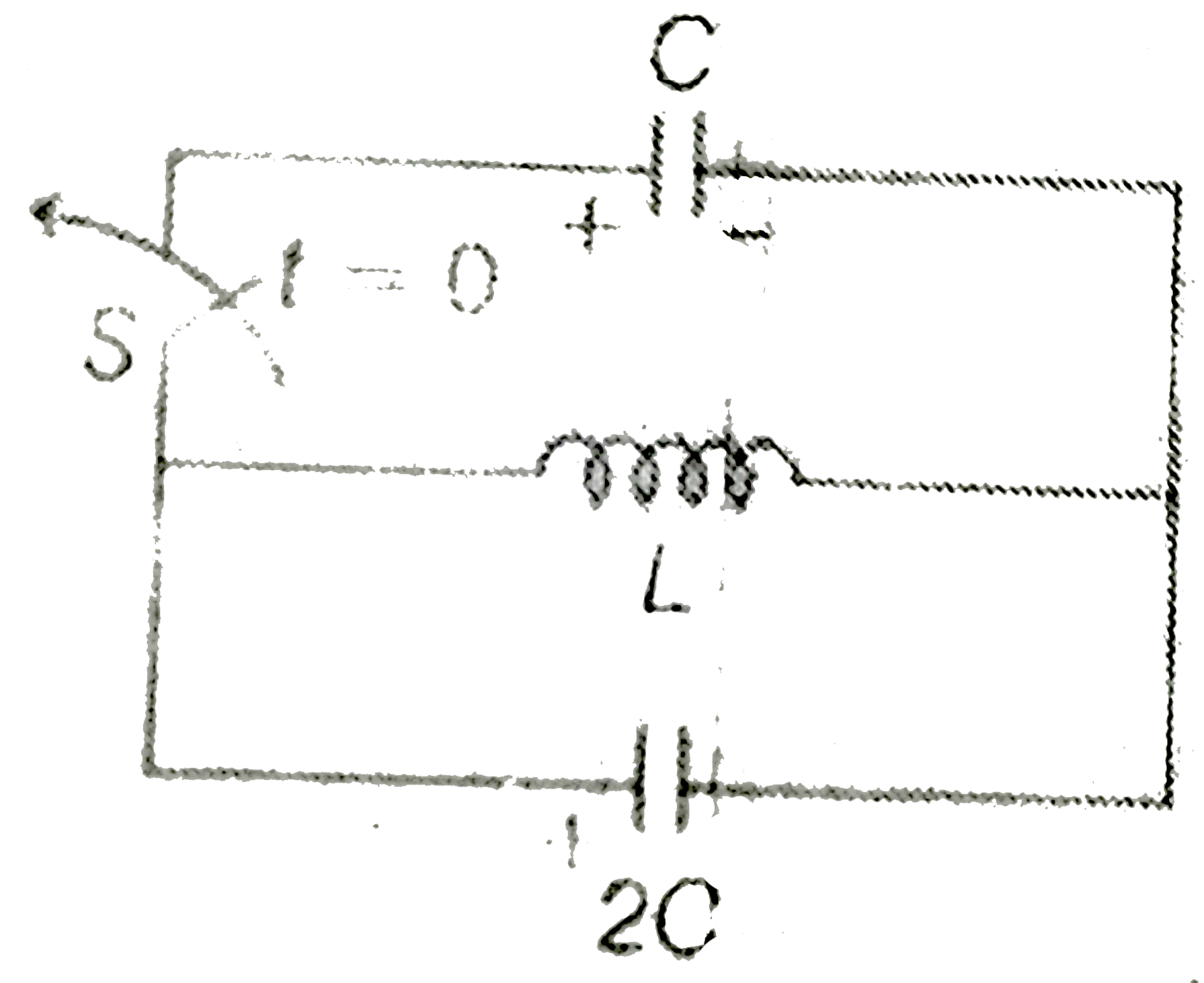 View Solution
View SolutionTwo capacitors A and B are connected in series with a battery as shown in the figure. When the switch S is closed and the two capacitors get charged fully, then
 View Solution
View SolutionTwo capacitors A and B are connected in series with a battery as shown in the figure. When the switch S is closed and the two capacitors get charged fully, then
 View Solution
View SolutionTwo capacitors A and B are connected in series with a battery as shown in the figure. When the switch S is closed and the two capacitors get charged fully, then
 View Solution
View SolutionThe switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
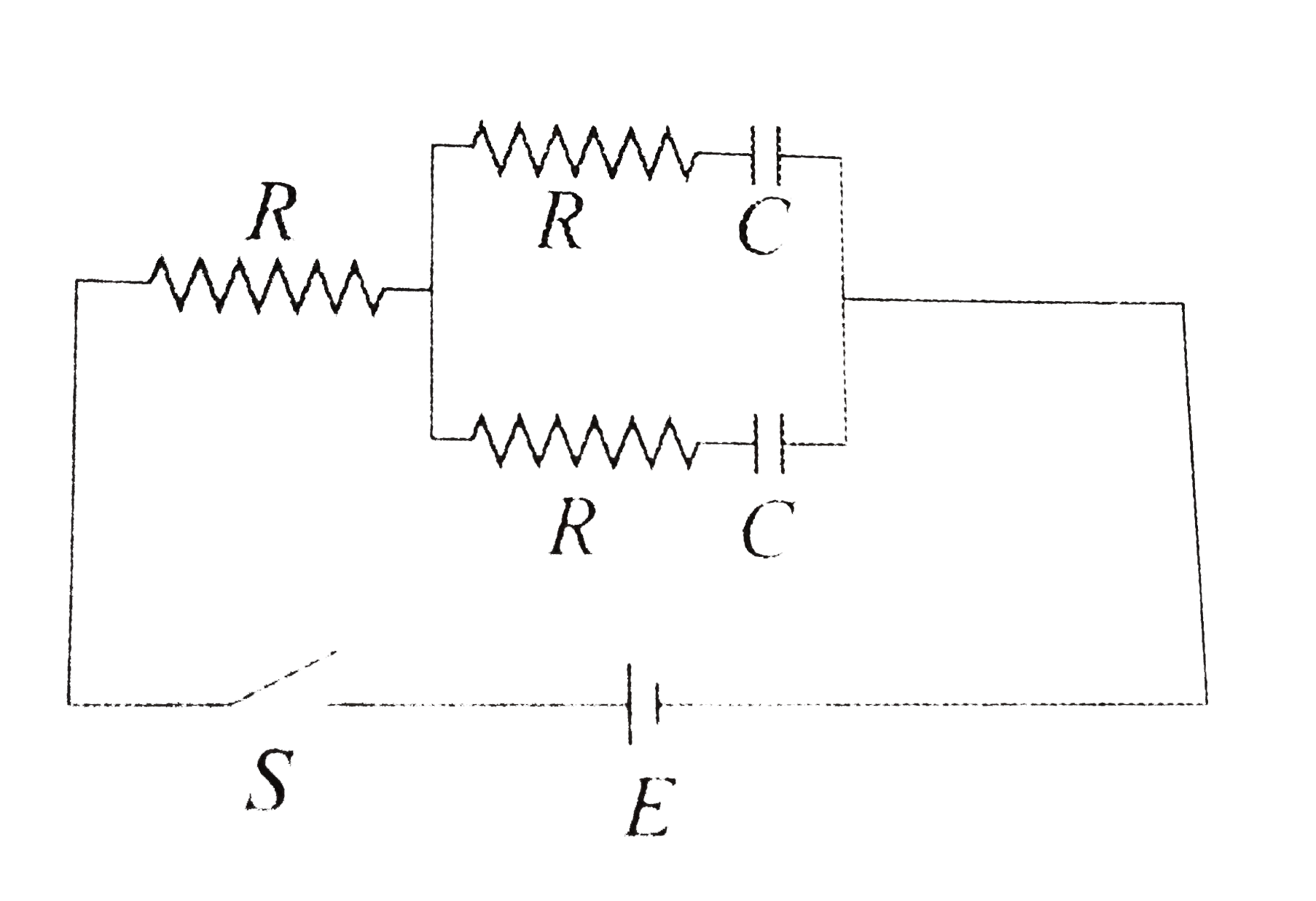 View Solution
View Solutionn the circuit shown in the figure, the capacitor C is charged to a potential Vo The heat generated and charge flow, in the circuit to when the switch S is closed, is
 View Solution
View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant
 View Solution
View Solution

