Two parallel wires carrying equal currents i1 and i2 with i1>i2. When the current are in the same direction, the 10mT. If the direction of i2 is reversed, the field becomes 30mT. The ratio i1/i2 is
The correct Answer is:2
To solve the problem, we need to analyze the magnetic fields produced by two parallel wires carrying currents i1 and i2.
Step 1: Understand the Magnetic Field from Each Wire
The magnetic field B at a distance D from a long straight wire carrying current I is given by the formula:
B=μ0I2πD
where μ0 is the permeability of free space.
Step 2: Calculate the Magnetic Field When Currents are in the Same Direction
When both currents i1 and i2 are in the same direction, the magnetic fields B1 and B2 at the midpoint (distance D from each wire) are:
B1=μ0i12πD
B2=μ0i22πD
Since i1>i2, the net magnetic field B is:
B=B1−B2=μ0i12πD−μ0i22πD=μ0(i1−i2)2πD
Given that this net magnetic field is 10mT:
μ0(i1−i2)2πD=10×10−3T(Equation 1)
Step 3: Calculate the Magnetic Field When Currents are in Opposite Directions
When the direction of i2 is reversed, the magnetic fields at the midpoint are:
B1=μ0i12πD
B2=μ0i22πD
Now, since the currents are in opposite directions, the net magnetic field B is:
B=B1+B2=μ0i12πD+μ0i22πD=μ0(i1+i2)2πD
Given that this net magnetic field is 30mT:
μ0(i1+i2)2πD=30×10−3T(Equation 2)
Step 4: Set Up the Ratio of the Two Equations
From Equation 1:
μ0(i1−i2)=20πD×10−3
From Equation 2:
μ0(i1+i2)=60πD×10−3
Step 5: Divide the Two Equations
Dividing Equation 2 by Equation 1:
i1+i2i1−i2=6020=3
Cross-multiplying gives:
i1+i2=3(i1−i2)
Expanding this:
i1+i2=3i1−3i2
Rearranging terms:
3i2+i2=3i1−i1
4i2=2i1
Thus:
i1i2=2
Final Answer
The ratio i1i2 is 2.
The magnetic field B at a distance D from a long straight wire carrying current I is given by the formula:
B=μ0I2πD
where μ0 is the permeability of free space.
When both currents i1 and i2 are in the same direction, the magnetic fields B1 and B2 at the midpoint (distance D from each wire) are:
B1=μ0i12πD
B2=μ0i22πD
Since i1>i2, the net magnetic field B is:
B=B1−B2=μ0i12πD−μ0i22πD=μ0(i1−i2)2πD
Given that this net magnetic field is 10mT:
μ0(i1−i2)2πD=10×10−3T(Equation 1)
When the direction of i2 is reversed, the magnetic fields at the midpoint are:
B1=μ0i12πD
B2=μ0i22πD
Now, since the currents are in opposite directions, the net magnetic field B is:
B=B1+B2=μ0i12πD+μ0i22πD=μ0(i1+i2)2πD
Given that this net magnetic field is 30mT:
μ0(i1+i2)2πD=30×10−3T(Equation 2)
From Equation 1:
μ0(i1−i2)=20πD×10−3
From Equation 2:
μ0(i1+i2)=60πD×10−3
Dividing Equation 2 by Equation 1:
i1+i2i1−i2=6020=3
Cross-multiplying gives:
i1+i2=3(i1−i2)
Expanding this:
i1+i2=3i1−3i2
Rearranging terms:
3i2+i2=3i1−i1
4i2=2i1
Thus:
i1i2=2
The ratio i1i2 is 2.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension
84 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
Similar Questions
Two parallel long wire carry currents i1 and i2 with i1>i2 . When the currents are in the same direction , the magnetic field midway between the wires is 10μT . When the direction of i2 is reversed, it becomes 40μT . The ratio i1/i2 is
View SolutionTwo parallel, long wires carry currents i1andi2 with i1>i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10mu T. If the direction of i2 is reversed, the field becomes 30mu T . The rationi1i2 is
View SolutionTwo parallel, long wires carry current i1 and i2 withi1>i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 30μT. If the direction of i1 is reversed , the field becomes 90μT. The ratio i1/i2 is
View SolutionTwo parallel, long wires carry currents i1andi2 with i1>i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10 μT. If the direction of i2 is reversed, the field becomes 30 μT. Find the ratio i1i2.
View SolutionTwo parallel long wires carry currents i1andi2 with i1>i2.When the currents are in the same direction then the magnetic field midway between the wires is 10μT. when the direction of i2 is reversed ,then it becomes 40μT. then ratio of i1/i2 is
View SolutionTwo long parallel straight conductors carry current i1 and i2(i1>i2). When the currents are in the same directions, the magnetic field at a point midway between the wires is 20μT. If the direction of i2 is reversed, the field becomes 50μT. The ratio of the current i1/i2 is :
View SolutionTwo long parallel wires carry currents i1 and i2 such that i1>i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 6×10−6T. If the direction of i2 is reversed, the field becomes 3×10−5T. The ratio i1i2 is
View SolutionTwo parallel long wires carry currents 18A and 3A. When the currents are in the same direction, the magnetic field at a point midway between the wire is B1. If the direction of i2 is reversed, the field becomes B2. Then the value of B1/B2 is
View SolutionIn the circuit shown, the currents i1 and i2 are
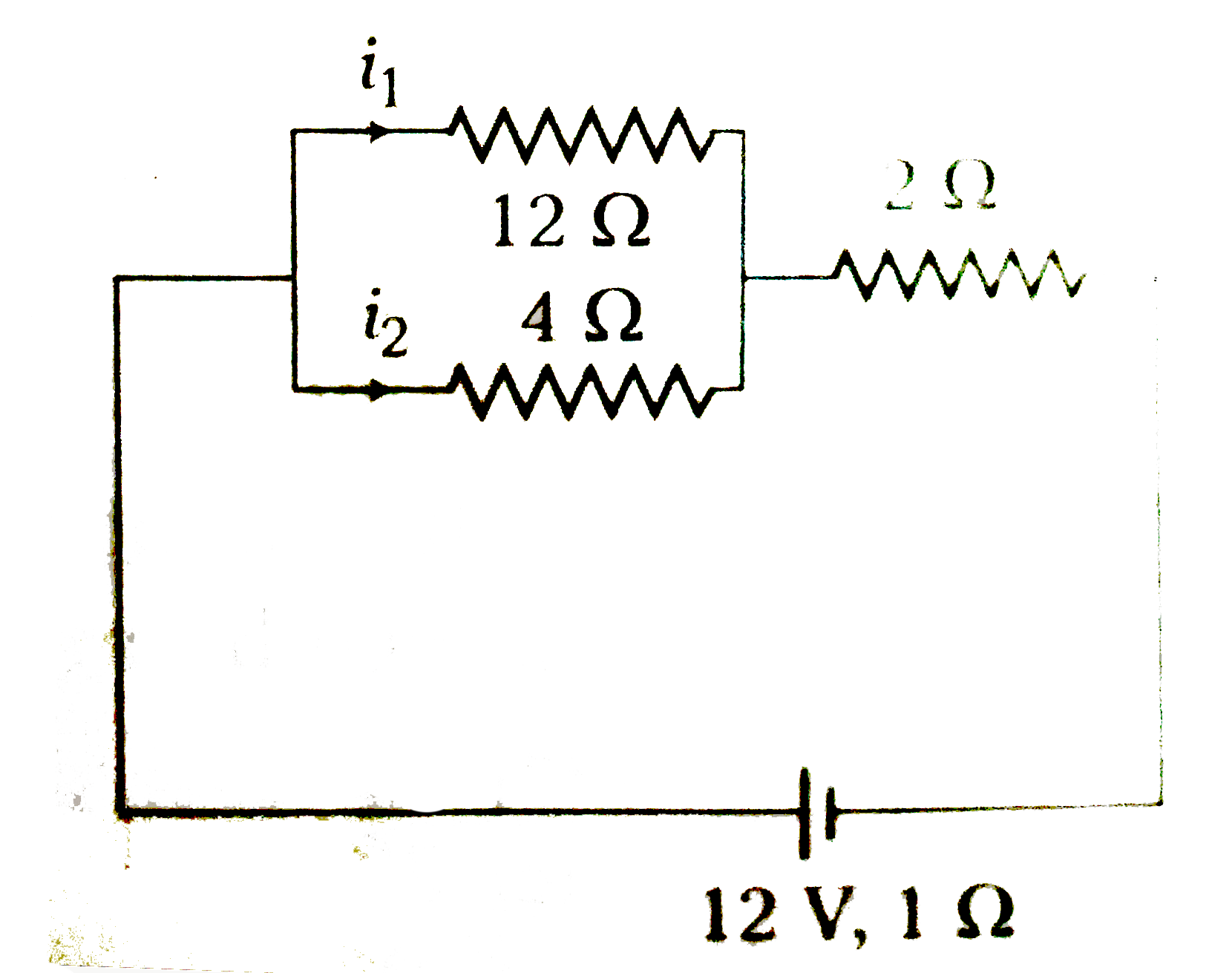
View SolutionTwo long wire AB abd CD carry currents i1 and i2 in the direactions show in figure

View Solution
