Two different ideal diatomic gases $A$ and $B$ are initially in the same state. $A$ and $B$ are then expanded to same final volume through adiabatic and isothermal process respectively. If $P_{A}, P_{B}$ and $T_{A}, T_{B}$ represents the final pressure and temperature of $A$ and $B$ respectively then.

A

$P_{A} < P_{B}$ and $T_{A} < T_{B}$

B

$P_{A} > P_{B}$ and $T_{A} > T_{B}$

C

$P_{A} > P_{B}$ and $T_{A} < T_{B}$

D

$P_{A} < P_{B}$ and $T_{A} > T_{B}$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:A

To solve the problem, we need to analyze the behavior of two different ideal diatomic gases, A and B, during their respective processes: adiabatic expansion for gas A and isothermal expansion for gas B.
1. Understand the Initial Conditions:
Both gases A and B are initially in the same state, meaning they have the same initial pressure (P₀), volume (V₀), and temperature (T₀).
2. Identify the Processes:
- Gas A undergoes an adiabatic expansion.
- Gas B undergoes an isothermal expansion.
3. Final Volume:
Both gases are expanded to the same final volume (V_f).
4. Analyze the Adiabatic Process (Gas A):
For an ideal gas undergoing adiabatic expansion, the relationship between pressure, volume, and temperature is given by:
$P_{f} V_{f}^{γ} = P_{0} V_{0}^{γ}$
where $γ$ (gamma) is the heat capacity ratio (C_p/C_v) for diatomic gases, which is approximately 1.4. Since the volume increases, the final pressure (P_A) will be lower than the initial pressure (P_0).
5. Analyze the Isothermal Process (Gas B):
For an ideal gas undergoing isothermal expansion, the pressure and volume relationship is given by:
$P_{f} V_{f} = P_{0} V_{0}$
Since the temperature remains constant during an isothermal process, the final pressure (P_B) will also be lower than the initial pressure, but the decrease will be less pronounced than in the adiabatic case.
6. Comparison of Final Pressures:
Since gas B is expanded isothermally and gas A is expanded adiabatically, the pressure of gas B (P_B) will be greater than the pressure of gas A (P_A) after expansion:
$P_{B} > P_{A}$
7. Determine Final Temperatures:
- For gas A (adiabatic), the temperature decreases as it expands, leading to a final temperature (T_A) that is lower than the initial temperature (T_0).
- For gas B (isothermal), the temperature remains constant, so the final temperature (T_B) is equal to the initial temperature (T_0).
8. Final Comparison:
- Since $P_{B} > P_{A}$ and $T_{B} = T_{0}$ while $T_{A} < T_{0}$ , we conclude:
$P_{B} > P_{A} and T_{B} > T_{A}$
Conclusion:
The final result is that the pressure of gas B is greater than that of gas A, and the temperature of gas B is greater than that of gas A.

Updated on:18/9/2024

|

Class 11 PHYSICS KINETIC THEORY OF GASES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Three vessels A,B,and C of different shapes contain a water upto the same height as shown in the figure . $P_{A}, P_{B}$ ,and $P_{C}$ be the pressure exerted by the water at the bottom of the vessels A ,B and C respectively . Then

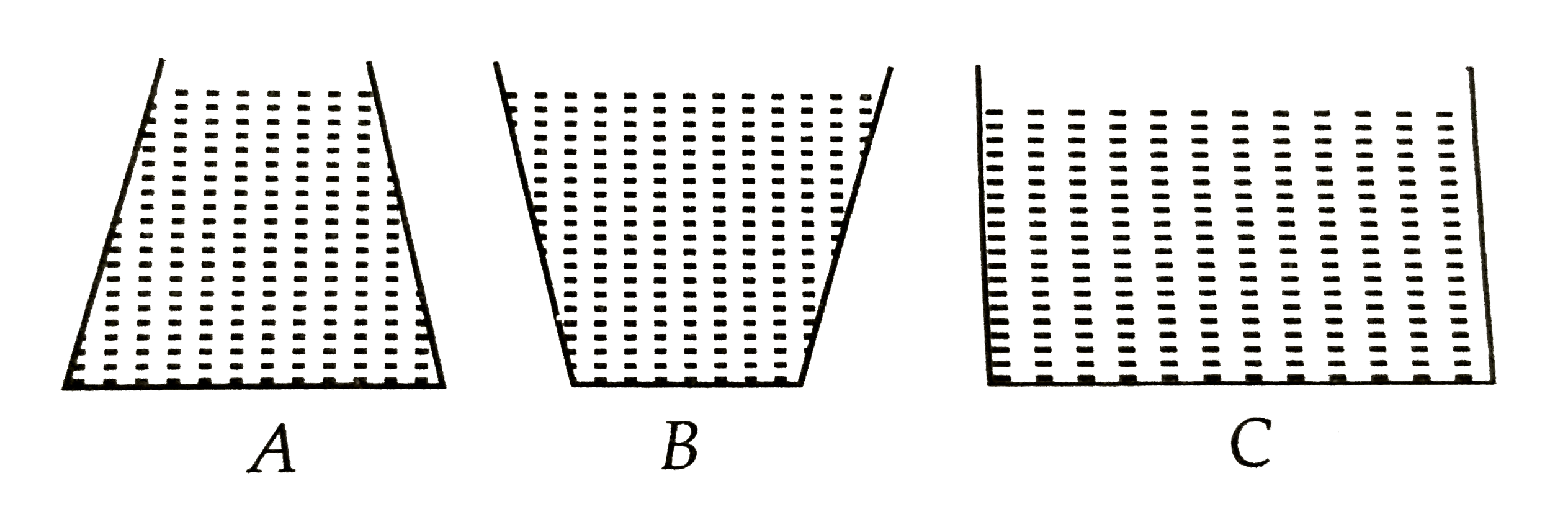A $P_{A} > P_{B} > P_{C}$
B $P_{B} > P_{C} > P_{A}$
C $P_{C} > P_{B} > P_{A}$
D $P_{A} = P_{B} = P_{C}$
Two samples, A and B of a gas at the same initial temperature and pressure are compressed from volume V to V/2, A isothermally and B adiabatically. The final pressure of A will be
Agreater than that of B
Bequal to that of B
Cless than of B
Dtwice that of B

CENGAGE PHYSICS ENGLISH-KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS-Single Correct

Home
Ask Doubt
Profile