Statement I: The work done on an ideal gas in changing its volume from V1 to V2 under a polytropic porcess is given by the integral ∫v2v1P.Dv taken along the process
Statement II: No work is done under an isochroci process of the gas.
(a)Statement I: is true, Statement II is true and Statement II is the correct explanation for Statement I.
(b)Statement I: is true, Statement II is true and Statement II is NOT the correct explanation for Statement I.
(c)Statement I is true, Statement II is false.
(d)Statement I is false, Statement II is fase.
The correct Answer is:C, D
To solve the question, we need to analyze both statements provided:
Step 1: Analyze Statement I
Statement I claims that the work done on an ideal gas in changing its volume from V1 to V2 under a polytropic process is given by the integral:
W=∫V2V1PdV
In a polytropic process, the pressure P can be expressed as a function of volume V. Therefore, the integral correctly represents the work done during the volume change from V1 to V2.
Conclusion for Statement I: This statement is True.
Step 2: Analyze Statement II
Statement II states that no work is done under an isochoric process of the gas.
In an isochoric process, the volume of the gas remains constant (V=constant). Since work done W is defined as:
W=PΔV
where ΔV is the change in volume. In an isochoric process, ΔV=0, hence:
W=P⋅0=0
Conclusion for Statement II: This statement is also True.
Step 3: Determine the Relationship Between the Statements
While both statements are true, we need to determine if Statement II provides a correct explanation for Statement I.
Statement I discusses the work done during a polytropic process, while Statement II discusses an isochoric process where no work is done. Thus, Statement II does not explain the work done in a polytropic process.
Final Conclusion:
- Statement I is True.
- Statement II is True, but it does not explain Statement I.
Final Answer
- Statement I: True
- Statement II: True, but not a correct explanation for Statement I.
---
Statement I claims that the work done on an ideal gas in changing its volume from V1 to V2 under a polytropic process is given by the integral:
Statement II states that no work is done under an isochoric process of the gas.
While both statements are true, we need to determine if Statement II provides a correct explanation for Statement I.
- Statement I is True.
- Statement II is True, but it does not explain Statement I.
- Statement I: True
- Statement II: True, but not a correct explanation for Statement I.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Comprehension56videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects29videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type14videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
The work done, W, during an isothermal process in which the gas expands from an intial volume V1, to a final volume V2 is given by (R : gas constant, T : temperature )
AR(V2−V1)logeT1T2BR(T2−T1)loge(V1V2)CRTloge[V2V1]D2RTloge[V1V2]
A sample of gas expands from volume V1 to V2. The amount of work done by the gas is greatest when the expansion is
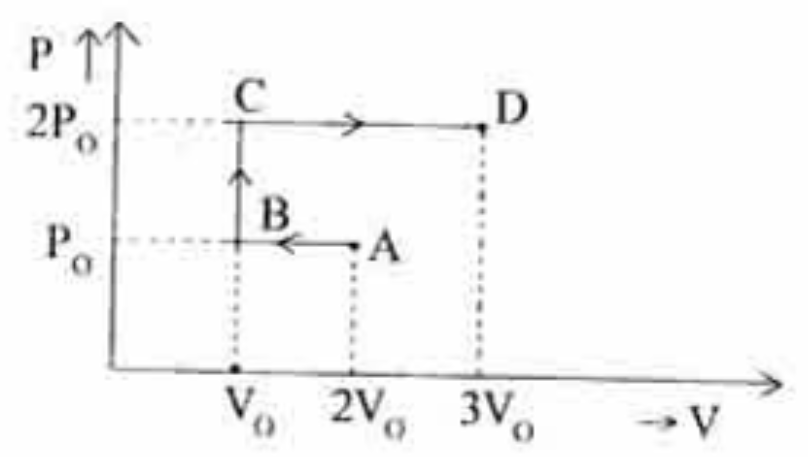
View SolutionP−V diagram of an ideal gas is as shown in figure. Work done by the gas in process ABCD is
 View Solution
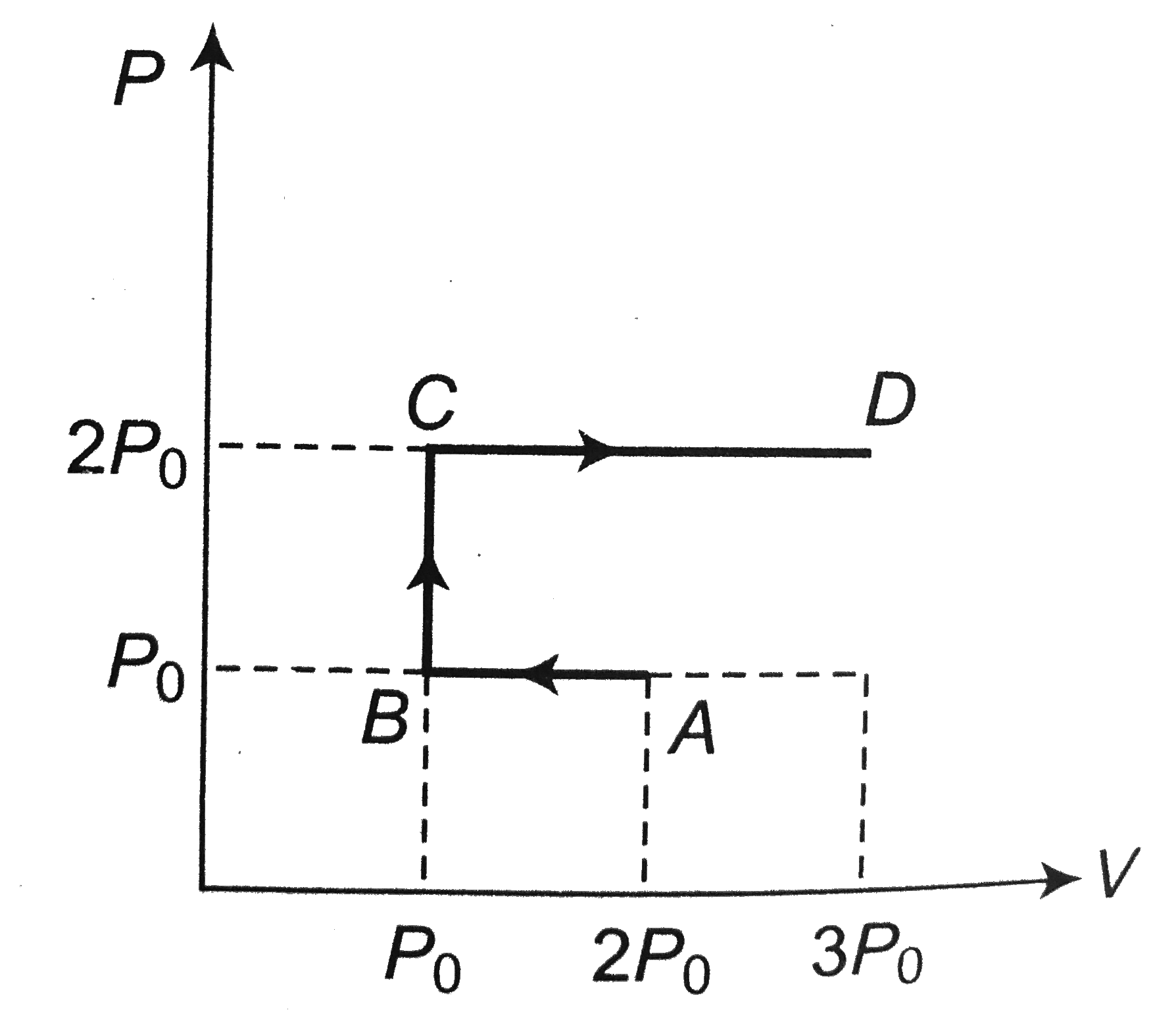
View SolutionP-V diagram of an ideal gas is as shown in figure. Work done by the gas in the process ABCD is
 View Solution
View SolutionPressure and volume of a gas changes from (p0V0) to (p04,2V0) in a process pV2= constant. Find work done by the gas in the given process.
View SolutionAn ideal gas expands isothermally from volume V1 to V2 and is then compressed to original volume V1 adiabatically. Initialy pressure is P1 and final pressure is P3. The total work done is W. Then
View SolutionAn ideal gas expands isothermally from volume V1 to V2 and is then compressed to original volume V1 adiabatically. Initialy pressure is P1 and final pressure is P3. The total work done is W. Then
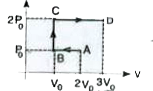
View SolutionP – V graph of an ideal gas is as shown in the diagram . Work done by the gas in the process ABCD is
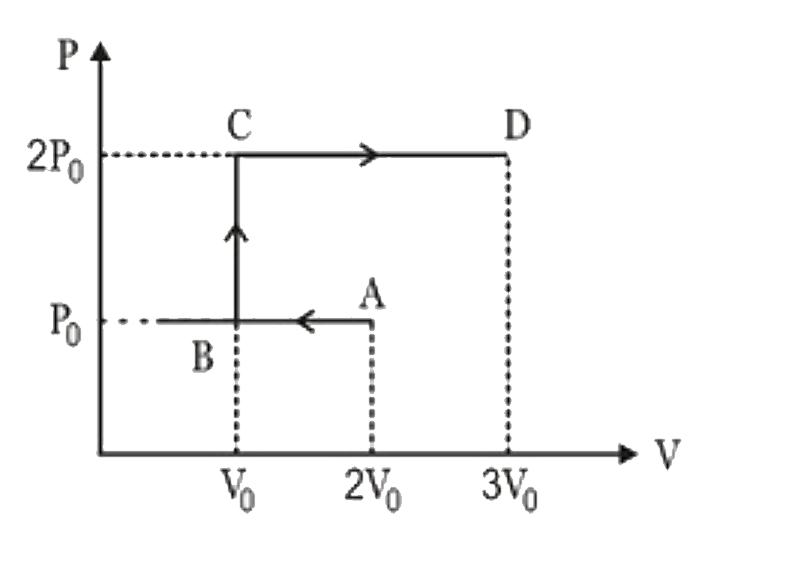 View Solution
View Solution