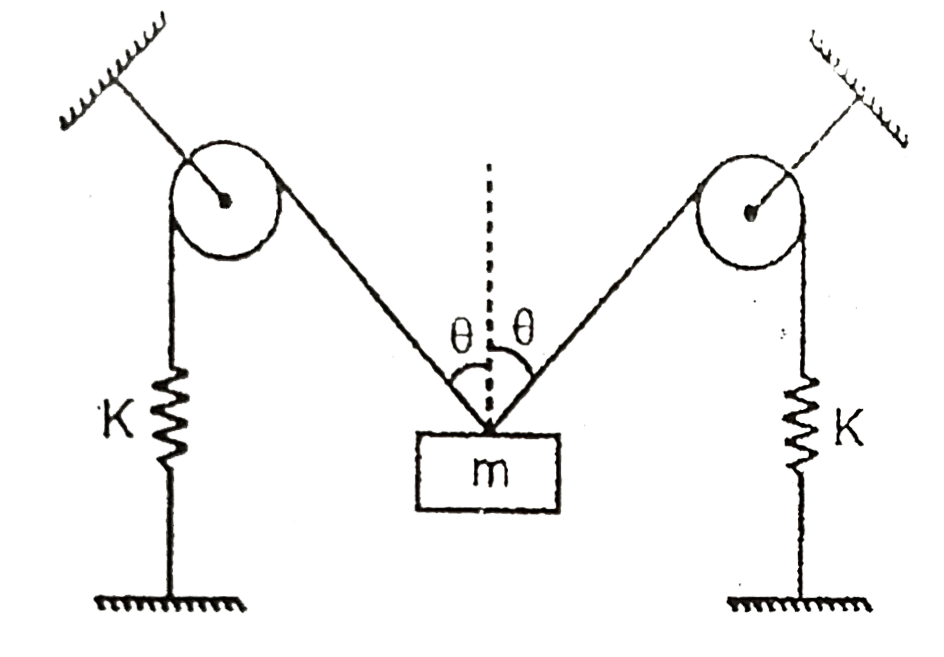
Consider a block symmetrically attached to two identical massless springs by means of strings passing over light frictionless pulleys as shown. In the equilibrium position extension in the springs is x0. Find the time period of small vertically oscillations of the blocks.
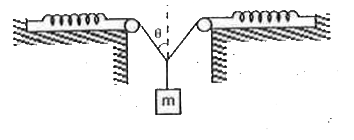
2π√x0gcosθ
Similar Questions
Knowledge Check
- Question 1 - Select One
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
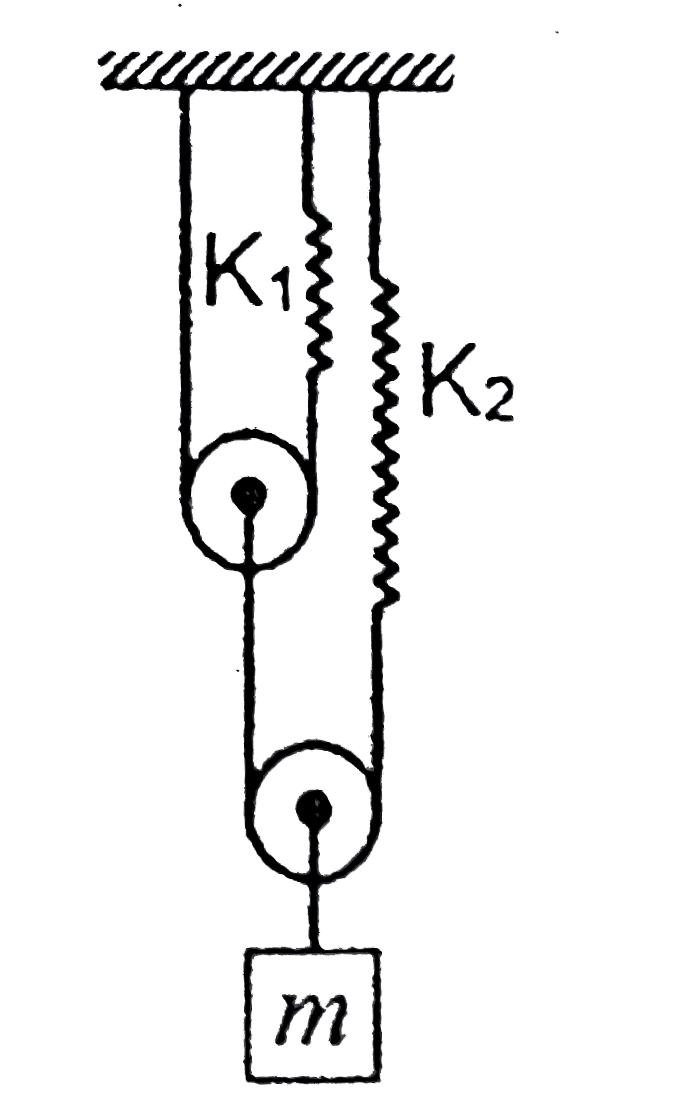
Find the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.
 View Solution
View SolutionIn the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
 View Solution
View SolutionIf two identical masses, attached by a light string passing over a light , frictionless pulley ( fixed ) of an Atwood's machine ( at different heights ) , are released from rest .
 View Solution
View SolutionTwo identical masses are attached by a light string that passes over a small pulley, as shown . The table and the pulley are frictionless. The hanging block is moving
 View Solution
View SolutionTwo identical springs are attached to a small block P. The other ends of the springs are fixed at A and B, When P is in equilibrium the extension of bottom spring is 10 cm. The period of small vertical oscillations of P about is equilibrium position is (useg=9.8m/s2)
 View Solution
View SolutionConsider the situation shown in the figure. A mass is hanging from a inextensible string which is passing over a pulley. The pulley itself is attached to a massless spring of stiffness k as shown in the figure. Find the time period of vertical oscillations of mass m if pulley is slightly displaced from its mean position. Assume that string does not slip over pulley.
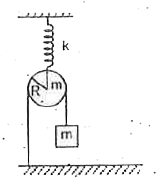 View Solution
View SolutionA block of mass M placed on a frictionless horizontal table is pulled by another block of mass m hanging vertically by a massless string passing over a frictionless pulley. The tension in the string is :
View Solution