A block is kept on a horizontal table. The stable is undergoing simple harmonic motion of frequency 3Hz in a horizontal plane. The coefficient of static friciton between block and the table surface is 0.72. find the maximum amplitude of the table at which the block does not slip on the surface.
3
1
2
7
The correct Answer is:c
To solve the problem step by step, we need to find the maximum amplitude of the table's simple harmonic motion such that the block does not slip off. Here’s how we can approach the solution:
Step 1: Identify the given values
- Frequency of motion, f=3Hz
- Coefficient of static friction, μs=0.72
- Acceleration due to gravity, g=10m/s2
Step 2: Calculate the angular frequency
The angular frequency ω can be calculated using the formula:
ω=2πf
Substituting the value of f:
ω=2π×3=6πrad/s
Step 3: Relate maximum acceleration to static friction
The maximum acceleration amax that can be sustained without slipping is given by:
amax=μsg
Substituting the values:
amax=0.72×10=7.2m/s2
Step 4: Relate maximum acceleration to amplitude
The maximum acceleration in simple harmonic motion is also given by:
amax=ω2A
Where A is the amplitude. Rearranging this equation gives:
A=amaxω2
Step 5: Substitute the values to find amplitude
Now substituting amax and ω:
A=7.2(6π)2
Calculating (6π)2:
(6π)2=36π2≈36×9.87≈355.32
Now substituting back:
A=7.2355.32≈0.0203m
Step 6: Convert to centimeters
To convert meters to centimeters:
A≈0.0203m×100=2.03cm
Final Answer
The maximum amplitude of the table at which the block does not slip on the surface is approximately:
2cm
- Frequency of motion, f=3Hz
- Coefficient of static friction, μs=0.72
- Acceleration due to gravity, g=10m/s2
The angular frequency ω can be calculated using the formula:
ω=2πf
Substituting the value of f:
ω=2π×3=6πrad/s
The maximum acceleration amax that can be sustained without slipping is given by:
amax=μsg
Substituting the values:
amax=0.72×10=7.2m/s2
The maximum acceleration in simple harmonic motion is also given by:
amax=ω2A
Where A is the amplitude. Rearranging this equation gives:
A=amaxω2
Now substituting amax and ω:
A=7.2(6π)2
Calculating (6π)2:
(6π)2=36π2≈36×9.87≈355.32
Now substituting back:
A=7.2355.32≈0.0203m
To convert meters to centimeters:
A≈0.0203m×100=2.03cm
The maximum amplitude of the table at which the block does not slip on the surface is approximately:
2cm
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A block is kept on a horizontal table. The table is undergoing simple farmonic motion of frequency 3Hz in a horizontal plane. The coefficient of static friction between the block and the table surface is 0.72. find the maximum amplitude of the table at which the block does not slip on the surface g=10ms−1
View SolutionA heavy uniform metal chain is kept on the surface of a horizontal table. The coefficient of friction between the chain and the table surface is 0.22. Find the maximum fraction of length of the chain that could hung over on one edge of the table ?
View Solution
Knowledge Check
A 20 N block is being pushed across a horizontal table by an 18 N force. If the coefficient of kinetic friction between the block and the table is 0.4, find the acceleration of the block.
A0.5m/s2B1m/s2C5m/s2D7.5m/s2A heavy uniform chain lies on horizontal table top. If the coefficient of friction between the chain and the table surface is 0.25, then the maximum fraction of the length of the chain that can hang over one edge of the table is
A0.2B0.25C0.35D0.15A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
A10NB5NC2.5ND20N
In the figure, a block of weight 60N is placed on a rough surface. The coefficient of friction between the block and the surface is 0.5. The minimum weight of the block does not slip on the surface is (x×10)N. The value of x is
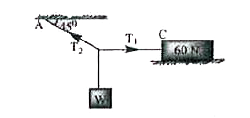
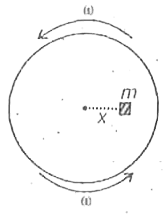
View SolutionA block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View SolutionA block on table shown in figure is just on the wedge of slipping. Find the coefficient of static friction between the block and table top.

View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
View Solution
