If the maximum speed and acceleration of a particle executing SHM is 20cm/sand100πcm/s2, find the time period od oscillation.
To solve the problem, we need to find the time period of oscillation for a particle executing Simple Harmonic Motion (SHM) given its maximum speed and maximum acceleration.
1. Identify the Given Values:
- Maximum Speed, Vmax=20cm/s
- Maximum Acceleration, Amax=100πcm/s2
2. Use the Formulas for SHM:
- The maximum speed in SHM is given by the formula:
Vmax=A⋅ω
where A is the amplitude and ω is the angular frequency.
- The maximum acceleration in SHM is given by:
Amax=A⋅ω2
3. Set Up the Equations:
- From the maximum speed equation:
A=Vmaxω
- From the maximum acceleration equation:
A=Amaxω2
4. Equate the Two Expressions for Amplitude:
- Setting the two expressions for A equal to each other:
Vmaxω=Amaxω2
5. Rearranging the Equation:
- Multiply both sides by ω2:
Vmax⋅ω=Amax
- Solving for ω:
ω=AmaxVmax
6. Substituting the Values:
- Substitute Amax=100πcm/s2 and Vmax=20cm/s:
ω=100π20=5πrad/s
7. Calculate the Time Period:
- The time period T is given by:
T=2πω
- Substitute ω=5π:
T=2π5π=25=0.4s
Final Answer:
The time period of oscillation is T=0.4s.
---
- Maximum Speed, Vmax=20cm/s
- Maximum Acceleration, Amax=100πcm/s2
- The maximum speed in SHM is given by the formula:
Vmax=A⋅ω
where A is the amplitude and ω is the angular frequency.
- The maximum acceleration in SHM is given by:
Amax=A⋅ω2
- From the maximum speed equation:
A=Vmaxω
- From the maximum acceleration equation:
A=Amaxω2
- Setting the two expressions for A equal to each other:
Vmaxω=Amaxω2
- Multiply both sides by ω2:
Vmax⋅ω=Amax
- Solving for ω:
ω=AmaxVmax
- Substitute Amax=100πcm/s2 and Vmax=20cm/s:
ω=100π20=5πrad/s
- The time period T is given by:
T=2πω
- Substitute ω=5π:
T=2π5π=25=0.4s
The time period of oscillation is T=0.4s.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
If maximum speed and acceleration of a particle executing SHM be 10cm/s and 100πcm/s2 respectively ,then find its time period.
Hint :vmax=Aω=10
amax=Aω2=100π
Solve to get ω
T=2πω
View SolutionThe maximum speed and acceleration of a particle executing simple harmonic motion are 10 cm s^-1 and 50 cms^-2. Find the position of the particle when the speed is 8cms^-1.
View SolutionMaximum acceleration of a particle in SHM is 16cm/s2 and maximum uelocity is 8cm/s.Find time period and amplitude of oscillations.
View Solutiona−x equation of a particle in SHM is a+4x=0
Here, a is in cm/s2 and x in cm.Find time period in second.
View SolutionThe maximum velocity of a particle, executing SHM with an amplitude 7 mm is 4.4 m/s. the period of oscillation is
View Solutiona−x equation of a body in SHM is a+16x=0. Here, x is in cm and a in cm/s2. Find time period of oscillations.
View SolutionAmplitude of a particle executing SHM is a and its time period is T. Its maximum speed is
View SolutionAcceleration of a particle in SHM at displacement x=10cm (from the mean position is a=−2.5cm/s2). Find time period of oscillations.
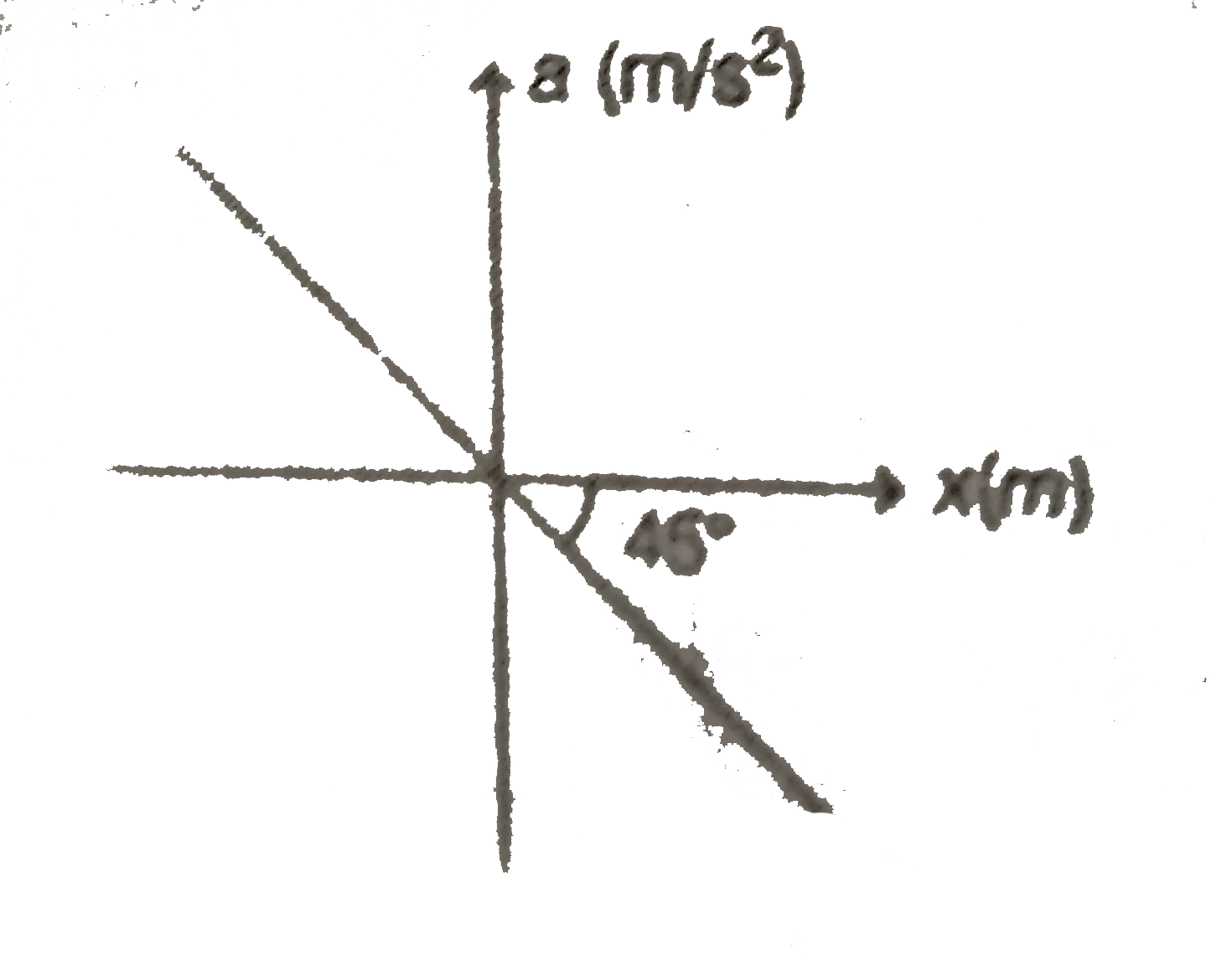
View SolutionAcceleration -displacemnet graph of a particle executing SHM is as shown in given figure. The time period of its oscillations is (in s)
View SolutionDisplacement of a particle executing SHM s x=10(cosπt+sinπt). Its maximum speed is
View Solution
