A particle starts SHM from mean position O executing SHM A and B are the two point at which its velocity is zero . It passes through a certain point P at time t1=0.5andt2=1.5s with a speed of 3m/s.
i. The maximum speed .......
ii. ratio AP/PB ....
 .
.
tOP=0.5s,tOBP=1.5s
Time taken from p is R is
1.5−0.52=0.5s
Time taken from O to B=0.5+0.5=1s
Hence time period =4s
Let x=Asinωt
⇒ω=2πT
=π2
ν=dxdt=Aωt
⇒νmax=Aω
Given ν=3m/satt=1/2s.
3=A×π2×cos(π2×12)
⇒A=6√2πcm
vmax=6√2π×π23√2m/s
xOP=Asinωt=6√2πsin(π2)×12=A√2
PA=A−A√2=A(√2−1)√2
PB=A(√2+1)√2
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A particle is executing SHM on a straight line. A and B are two points at which its velocity is zero. It passes through a certain point P(APltBP) at successive intervals of 0.5s and 1.5 s with a speed of 3m/s.
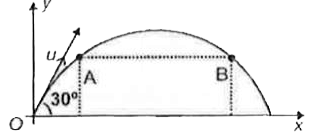
View SolutionA particle is thrown with a velocity of u m/s. it passes A and B as shown in figure at time t1=1 s andt2=3 s . The value of u is (g = 10 m/s2)
View SolutionA and B are two points on the path of a particle executing SHM in a straight line, at which its velocity is zero. Starting from a certain point X (AX<BX) the particle crosses this pint again at successive intervals of 2 seconds and 4 seconds with a speed of 5m/s
Q. The ratio AXBX is
View SolutionX1 and X2 are two points on the path of a particle executing SHM in a straight line, at which its velocity is zero. Starting from a certain point X(X1X<X2X) then particle crosses this point again at successive intervals of 2s and 4s with a speed of 5m/s.
The time period of SHM is
View SolutionA body is executing SHM with an amplitude of 0.1 m. Its velocity while passing through the mean position is 3ms−1. Its frequency in Hz is
View SolutionA and B are two points on the path of a particle executing SHM in a straight line, at which its velocity is zero. Starting from a certain point X (AX<BX) the particle crosses this pint again at successive intervals of 2 seconds and 4 seconds with a speed of 5m/s
Q. Amplitude of oscillation is
View SolutionA particle of mass 2kg executing SHM has amplitude 20cm and time period 1s. Its maximum speed is
View SolutionA particle starts to move in a straight line from a point with velocity 10 m s−1 and acceleration - 2.0 ms−2. Find the position and velocity of the particle at (i) t = 5 s, (ii) t' = 10 s.
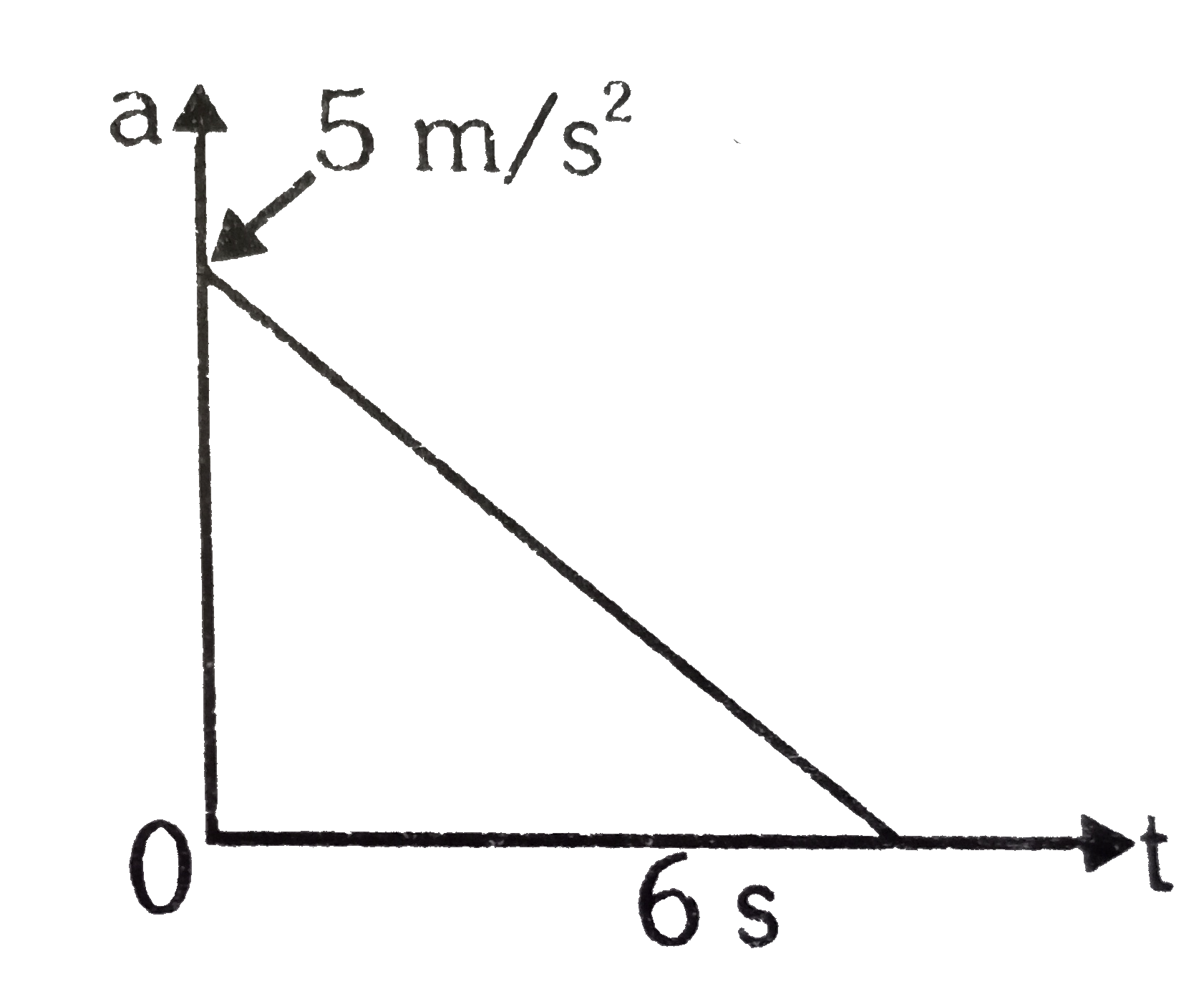
View SolutionA particle starts from rest. Its acceleration at time t=0 is 5m/s2 which varies with time as shown in the figure. The maximum speed of the particle will be
View SolutionA particle executes shm in a line 10 cm long. When it passes through the mean position its velocity is 15cms−1 . Find the period.
View Solution
