For a particle moving in straight line with increasing speed the appropriate sign of acceleration a and velocity v can be:
a>0 and v>0
a<0 and v<0
a>0 and v<0
a<0 and v>0
The correct Answer is:A, B
To determine the appropriate signs of acceleration a and velocity v for a particle moving in a straight line with increasing speed, we can analyze the relationship between velocity and acceleration.
1. Understanding Velocity and Acceleration:
- Velocity (v) indicates the speed and direction of the particle.
- Acceleration (a) indicates the rate of change of velocity. It can be positive (speeding up) or negative (slowing down).
2. Case 1: Both Velocity and Acceleration are Positive:
- If v>0 and a>0, the particle is moving in the positive direction and speeding up.
- This scenario leads to an increase in speed.
- Conclusion: This case is valid.
3. Case 2: Both Velocity and Acceleration are Negative:
- If v<0 and a<0, the particle is moving in the negative direction and speeding up (in the negative direction).
- This also results in an increase in speed (though the speed is considered negative).
- Conclusion: This case is also valid.
4. Case 3: Positive Acceleration and Negative Velocity:
- If v<0 and a>0, the particle is moving in the negative direction but experiencing positive acceleration.
- This means the particle is slowing down (decelerating) in the negative direction, which results in a decrease in speed.
- Conclusion: This case is invalid.
5. Case 4: Negative Acceleration and Positive Velocity:
- If v>0 and a<0, the particle is moving in the positive direction but experiencing negative acceleration.
- This means the particle is slowing down, which results in a decrease in speed.
- Conclusion: This case is also invalid.
Final Conclusion:
The valid cases where the particle is moving in a straight line with increasing speed are:
- Both a and v are positive.
- Both a and v are negative.
Thus, the correct options are:
- Option A: a>0, v>0
- Option B: a<0, v<0
- Velocity (v) indicates the speed and direction of the particle.
- Acceleration (a) indicates the rate of change of velocity. It can be positive (speeding up) or negative (slowing down).
- If v>0 and a>0, the particle is moving in the positive direction and speeding up.
- This scenario leads to an increase in speed.
- Conclusion: This case is valid.
- If v<0 and a<0, the particle is moving in the negative direction and speeding up (in the negative direction).
- This also results in an increase in speed (though the speed is considered negative).
- Conclusion: This case is also valid.
- If v<0 and a>0, the particle is moving in the negative direction but experiencing positive acceleration.
- This means the particle is slowing down (decelerating) in the negative direction, which results in a decrease in speed.
- Conclusion: This case is invalid.
- If v>0 and a<0, the particle is moving in the positive direction but experiencing negative acceleration.
- This means the particle is slowing down, which results in a decrease in speed.
- Conclusion: This case is also invalid.
The valid cases where the particle is moving in a straight line with increasing speed are:
- Both a and v are positive.
- Both a and v are negative.
- Option A: a>0, v>0
- Option B: a<0, v<0
Similar Questions
If a particle is moving along straight line with increasing speed, then
View SolutionThe speed of a particle moving in a circle is increasing. The dot product of its acceleration and velocity is
View SolutionVelocity (v) versus displacement (s) graph of a particle moving in a straight line is shown in figure. Corresponding acceleration (a) versus velocity (v) graph will be
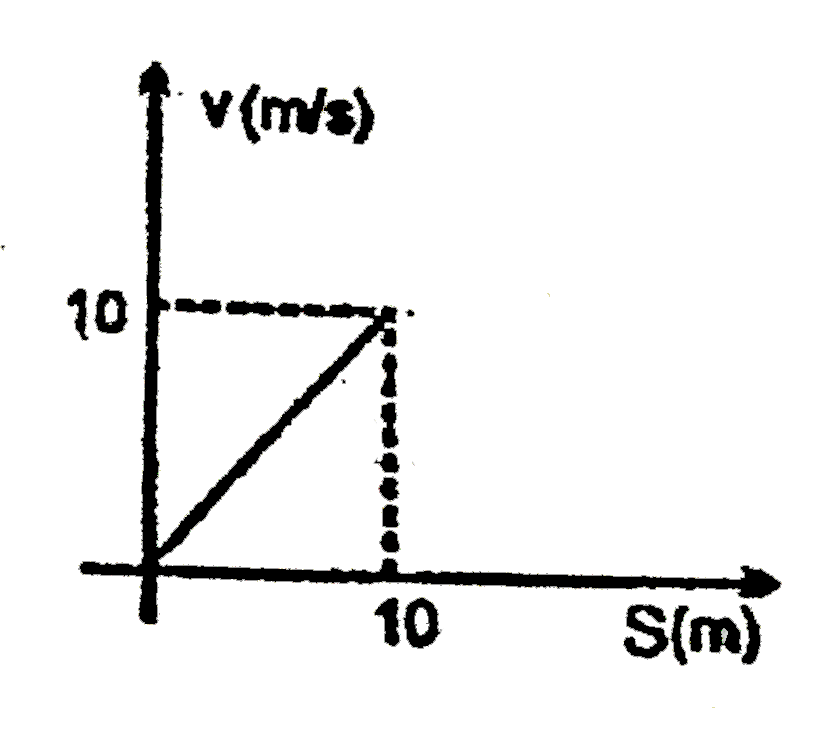 View Solution
View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionVelocity versus displacement graph of a particle moving in a straight line as shown in figure.
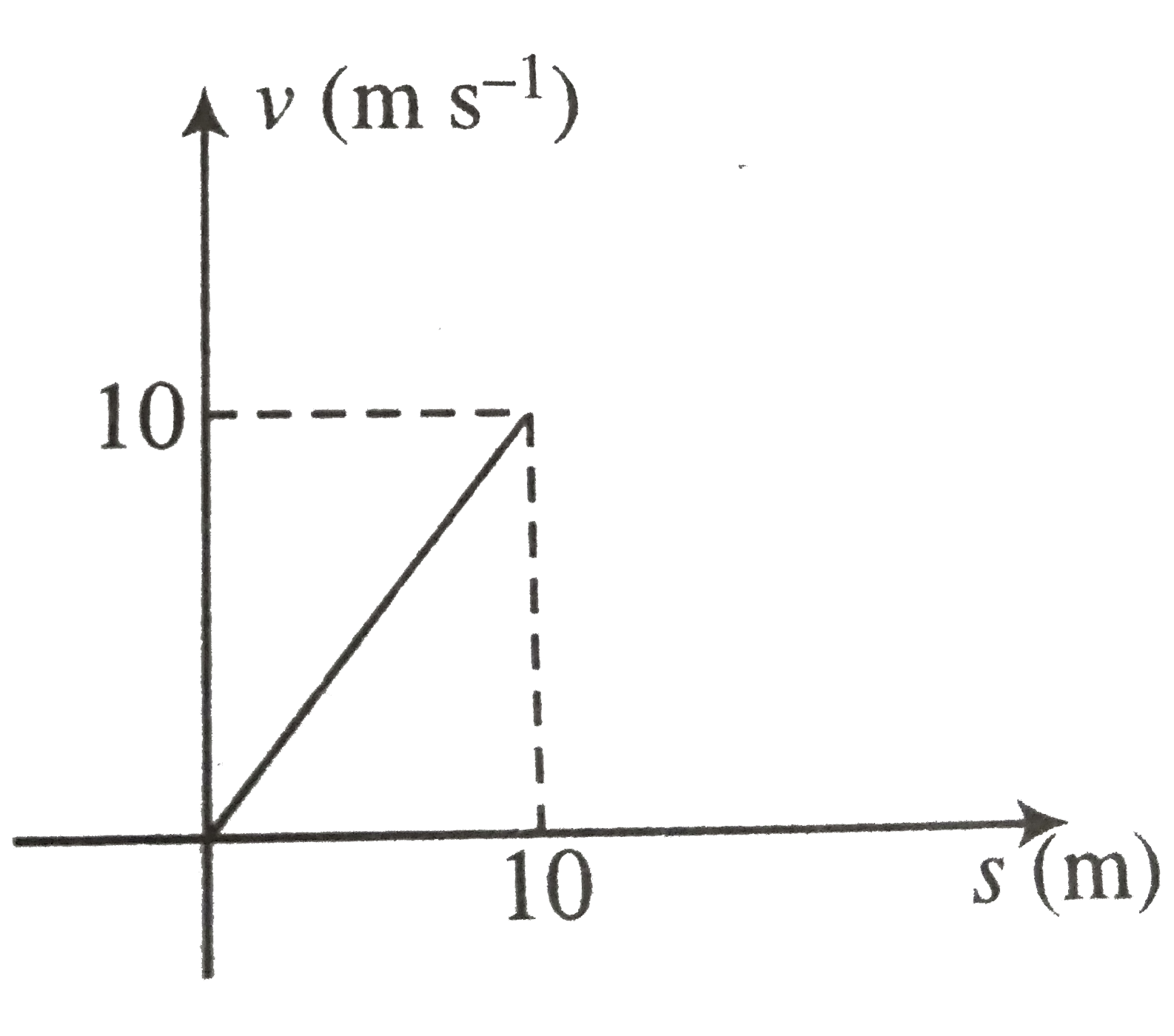
The corresponding acceleration versus velocity graph will be .View Solution
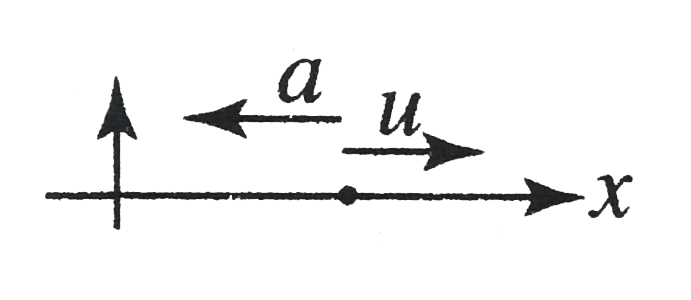
For a particle moving along straight line with constant acceleration (a), we define velocity of the particle with time as
v=u+at, (u=initial velocity)
Draw the velocity-time graph of the particle in following situations.
(i) Velocity is decresing with time (i.e., acceleration in negative)
(ii) Initial velocity is negative but acceleration is positiveView SolutionA : For a particle moving in a straight line, its acceleration must be either parallel or antiparallel to velocity.
R : A body moving along a curved path may have constant acceleration.View SolutionThe velocity of a particle moving in a straight line is decreasing at the rate of 3m/s per metre of displacement at an instant when the velocity is 10m/s. Determine the acceleration of the particle at this instant.
View SolutionDisplacement-time graph of a particle moving in a straight line is as shown in figure.
Find the sign of velocity and acceleration in regions oa,ab, bc and cd.
 View Solution
View Solution

