Question

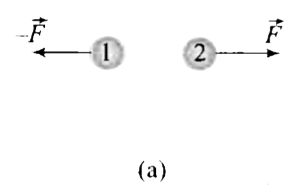
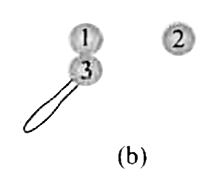
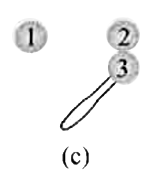
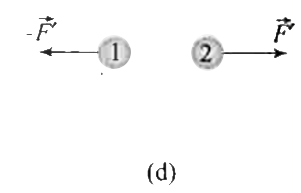
Indentical isolated conduction sphers 1 and 2 have equal charges and are separated by a distance that is large compared with their diameters (Fig.a). The electrostatic force acting on spkhere 2 due to sphere 1 is F. Suppose now that a third identical sphere 3, having an insulation handle and initially neutral, is touched first to sphere 1 (Fig. b), then to sphere 2 (Fig. c), and dinally removed (Fig. d). The electrostatic force that now acts on sphere 2 has magnitude F'. What is the ${\displaystyle \frac{F\prime }{F}}$?

Options

A.
B.
C.
D.

Answer

C

Explanation

To solve the problem, we will analyze the situation step by step:

Step 1: Initial Setup
We have two identical isolated conducting spheres, Sphere 1 and Sphere 2, each with an equal charge \( q \). The electrostatic force \( F \) acting on Sphere 2 due to Sphere 1 is given by Coulomb's law:

\( F = k \frac{q \cdot q}{r^2} = k \frac{q^2}{r^2} \)

where \( k \) is Coulomb's constant and \( r \) is the distance between the centers of the two spheres.

Hint: Remember that the force between two point charges is given by Coulomb's law.

Step 2: Touching Sphere 3 to Sphere 1
Sphere 3 is initially neutral and is touched to Sphere 1. When Sphere 3 touches Sphere 1, charge will redistribute. The total charge before touching is \( q + 0 = q \). After touching, the charge will be equally distributed between Sphere 1 and Sphere 3:

\( \text{Charge on Sphere 1} = \frac{q + 0}{2} = \frac{q}{2} \)
\( \text{Charge on Sphere 3} = \frac{q + 0}{2} = \frac{q}{2} \)

Hint: When two conductors touch, charge redistributes equally because they are identical.

Step 3: Touching Sphere 3 to Sphere 2
Next, Sphere 3 (now with charge \( \frac{q}{2} \)) is touched to Sphere 2, which has charge \( q \). The total charge when they touch is:

\( \text{Total charge} = q + \frac{q}{2} = \frac{3q}{2} \)

After touching, this charge will also redistribute equally between Sphere 2 and Sphere 3:

\( \text{Charge on Sphere 2} = \text{Charge on Sphere 3} = \frac{3q/2}{2} = \frac{3q}{4} \)

Hint: Again, charge redistributes equally when two identical conductors touch.

Step 4: Calculating the New Force \( F' \)
Now, we need to calculate the new force \( F' \) acting on Sphere 2 due to Sphere 1. Sphere 1 now has a charge \( \frac{q}{2} \) and Sphere 2 has a charge \( \frac{3q}{4} \). The force \( F' \) is given by:

\( F' = k \frac{\left(\frac{q}{2}\right) \left(\frac{3q}{4}\right)}{r^2} = k \frac{3q^2}{8r^2} \)

Step 5: Finding the Ratio \( \frac{F'}{F} \)
Now we can find the ratio of the new force \( F' \) to the original force \( F \):

\( \frac{F'}{F} = \frac{k \frac{3q^2}{8r^2}}{k \frac{q^2}{r^2}} = \frac{3}{8} \)

Final Answer
Thus, the ratio \( \frac{F'}{F} \) is:

\( \frac{F'}{F} = \frac{3}{8} \)

---