Two positive point charges each of magnitude 10C are fixed at positions A &B at a seperation 2d=6m. A negatively charged particle of mass m=90gm and charge of magnitude 10×10−6C is revolving in a circular path of radius 4m in the plane perpendicular to the line AB and bisecting the line AB. Neglect the effect of gravity. Find the angular velocity of the particle
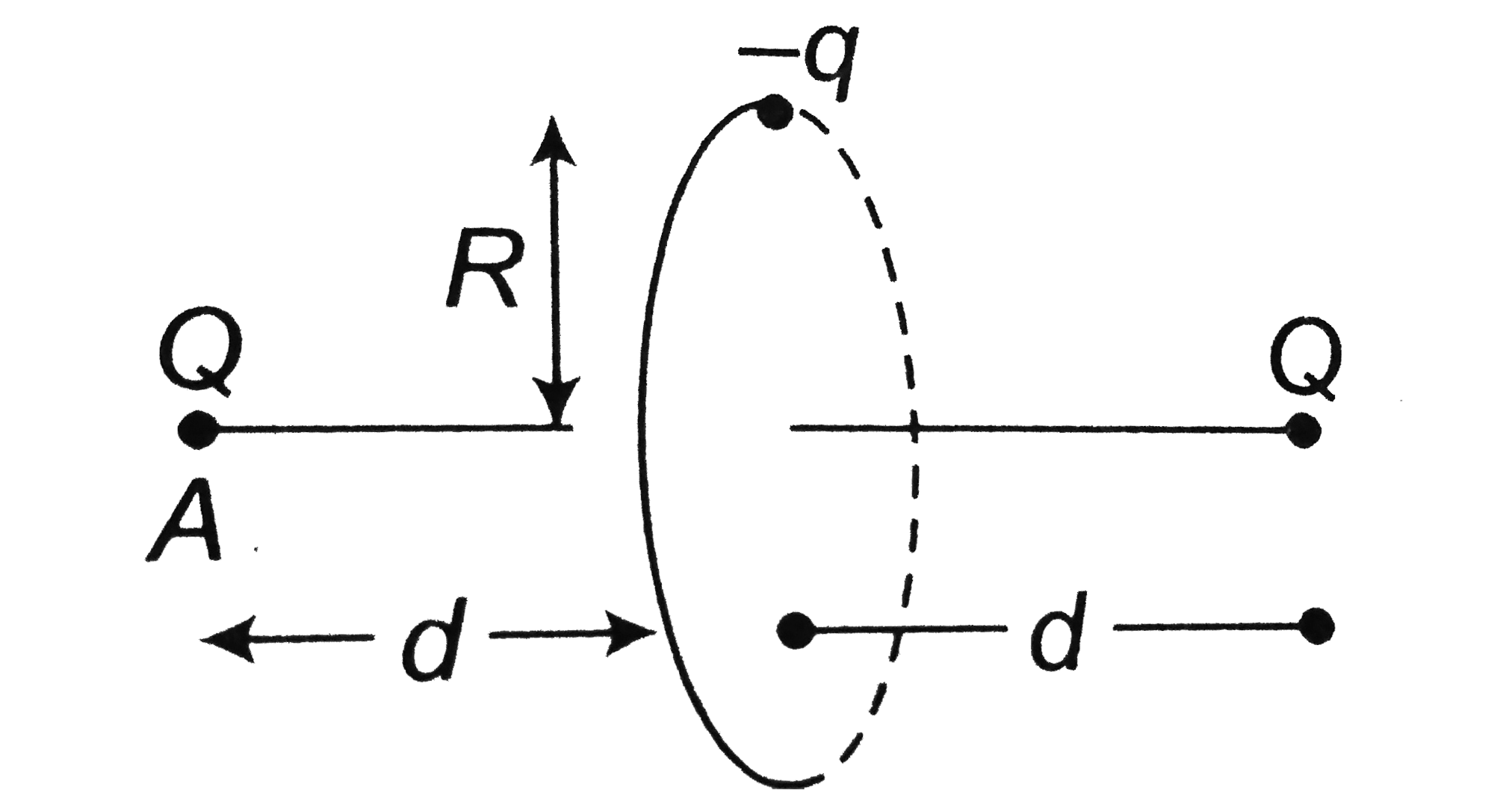
The correct Answer is:400 rad /S3 No
Step by step video & image solution for Two positive point charges each of magnitude 10 C are fixed at positions A &B at a seperation 2d= 6m. A negatively charged particle of mass m= 90gm and charge of magnitude 10xx10^(-6)C is revolving in a circular path of radius 4m in the plane perpendicular to the line AB and bisecting the line AB. Neglect the effect of gravity. Find the angular velocity of the particle by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective
32 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct
47 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises
58 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
A particle of mass m carrying charge '+q1' is revolving around a fixed charge '−q2' in a circular path of radius r. Calculate the period of revolution.
View SolutionA particle of mass m carrying a charge −q1 starts moving around a fixed charge +q2 along a circulare path of radius r. Find the time period of revolution T of charge −q1.
View SolutionA water particle of mass 10.0 mg and having a charge of 1.50×10−6C stays suspended in a room. What is the magnitude of electric field in the room ? What is its direction?
View SolutionA positive charge .Q. is fixed at a point, A negatively charged of mass .m. and charge .q. is revolving in a circular path of radius radius r1 with .Q. as the centre. The change in potential energy to change the radius of the circular path from r1andr2 in joule is
View SolutionConsider two positive point charges, each of magnitude q, placed on the y-axis at the points (0, a) and (0, -a). A positively charged particle of charge q' and mass m is displaced slightly from the origin in the direction of the positive x-axis.
Speed of charge q' at infinity is
View SolutionConsider two positive point charges, each of magnitude q, placed on the y-axis at the points (0, a) and (0, -a). A positively charged particle of charge q' and mass m is displaced slightly from the origin in the direction of the positive x-axis.
At the origin, charge q' will be in
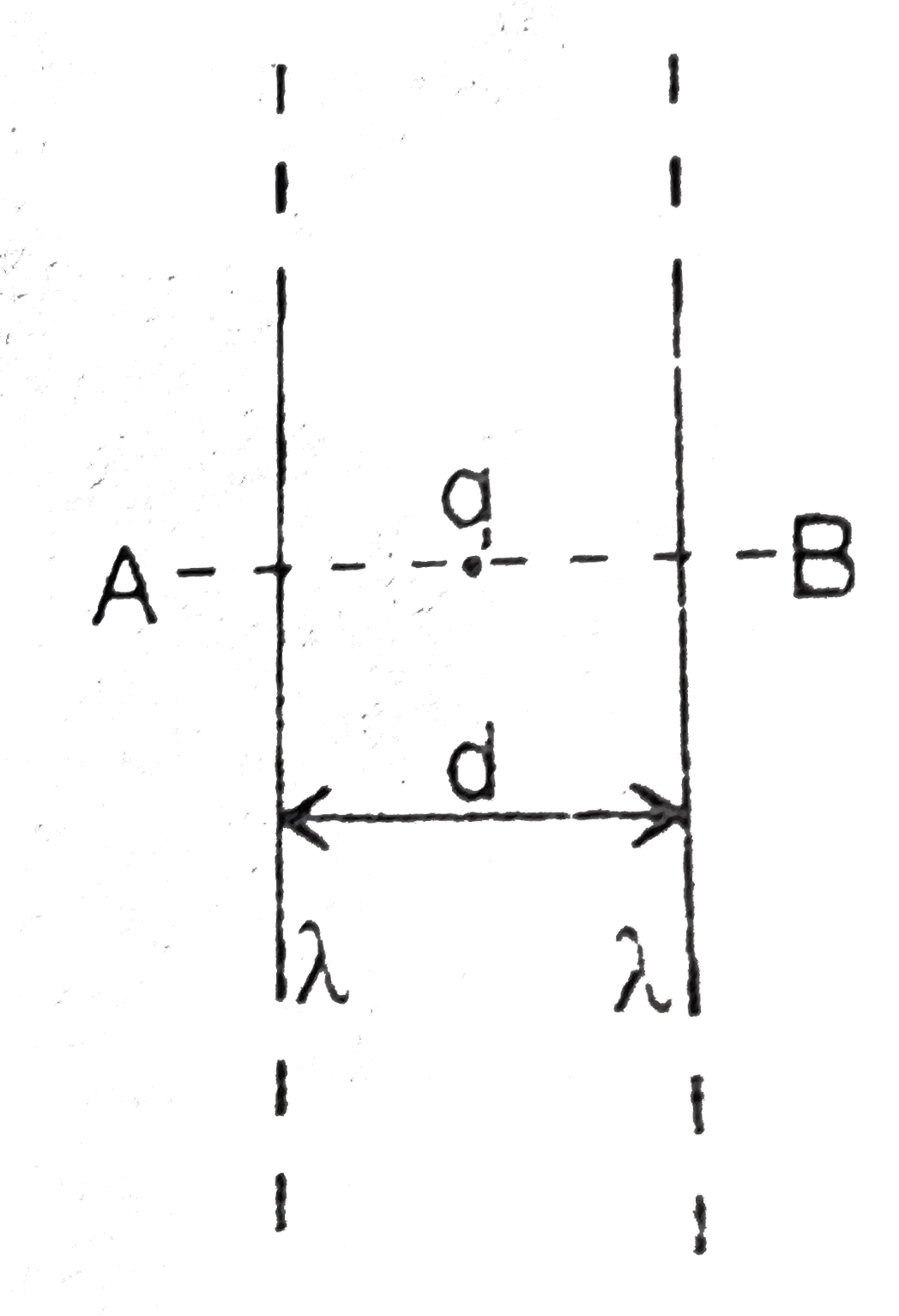
View SolutionTwo infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
View SolutionTwo identical charges, 5μC each are fixed at a distance 8 cm and a charged particle of mass 9×10−6kg and charge −10μC is placed at a distance 5 cm from each of them and is released. Find the speed of the particle when it is nearest to the two charges.
View SolutionTwo positively charged small particles, each of mass 1.7×10−27kg and carrying a charge of 1.6×10−19C are placed apart at a separation r. If each one experiences a repulsive force equal to its weight find their separation.
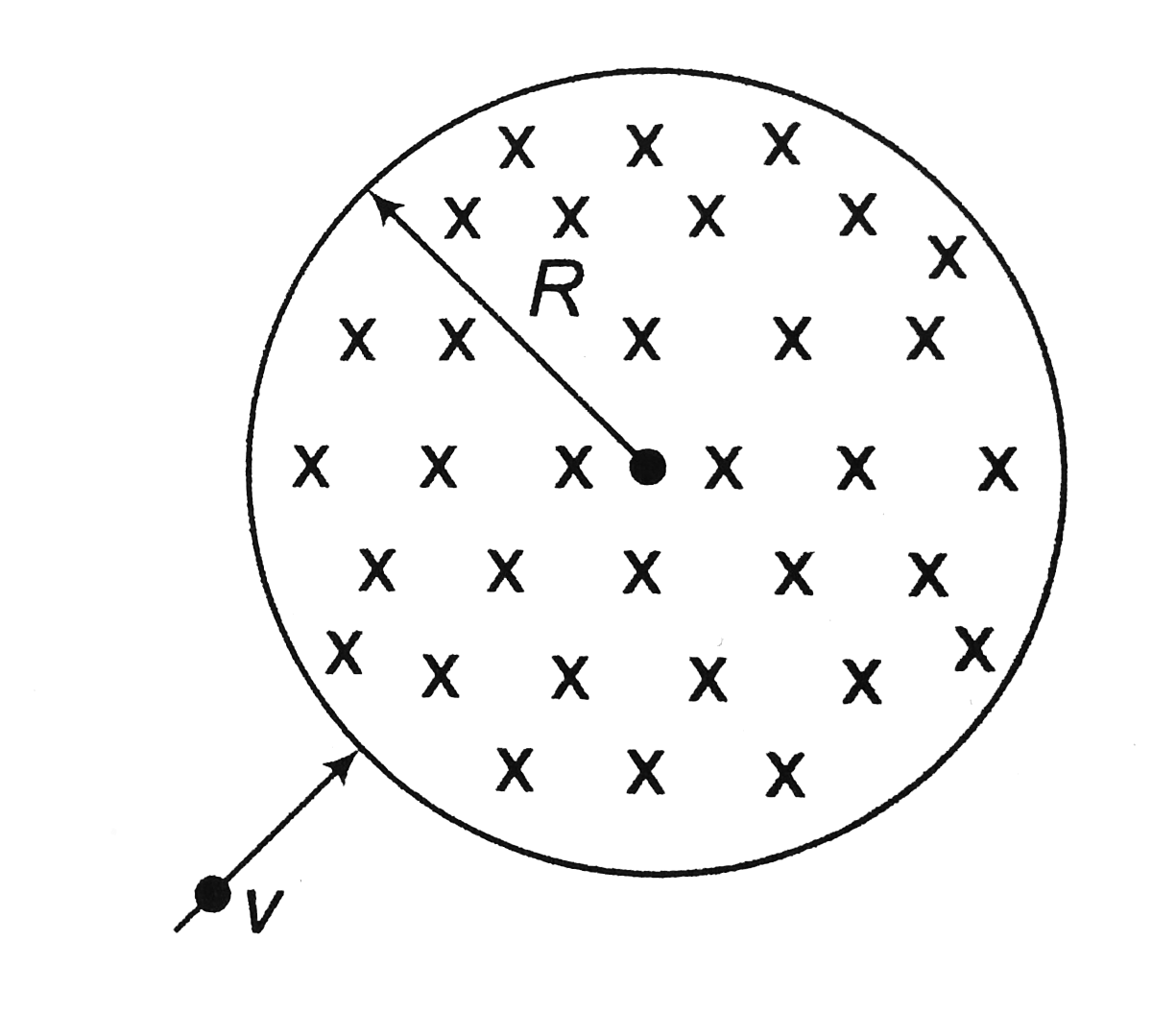
View SolutionA particle of mass m having a charge q enters into a circular region of radius R with velocity v directed towards the centre. The strength of magnetic field is B. Find the deviation in the path of the particle.
View Solution
