Four point positive charges are held at the vertices of a square in a horizontal plane. Their masses are 1kg,2kg,3kg,&4kg. Another point positive charge of mass 10kg is kept on the axis of the sqaure. The weight of their fifth charge is balanced by the electrostatic force due to those four charges. If the four charge on the vertices are released such that they can freely move in any direction(vertical, horizontal etc.) then the acceleration of the centres of mass of the four charges immediately after the release is (Use g=10m/s2)
The correct Answer is:20m/s2 downwards
To solve the problem step by step, we will follow the reasoning provided in the video transcript while ensuring clarity and completeness in our explanation.
Step 1: Understand the System
We have four point positive charges located at the vertices of a square and a fifth charge of mass 10 kg placed on the axis of the square. The four charges have masses of 1 kg, 2 kg, 3 kg, and 4 kg. The weight of the fifth charge is balanced by the electrostatic force due to the four charges.
Step 2: Calculate the Weight of the Fifth Charge
The weight of the fifth charge (mass = 10 kg) can be calculated using the formula:
W=mg
Where g=10m/s2.
W=10kg×10m/s2=100N
Step 3: Determine the Electrostatic Force
Since the weight of the fifth charge is balanced by the electrostatic force (Fe) from the four charges, we have:
Fe=W=100N
Step 4: Calculate the Total Force Acting on the System
When the four charges are released, they will experience a net force due to their mutual repulsion. The total force acting on the center of mass of the four charges can be considered as the sum of their individual forces. Since they are all positive charges, they will repel each other.
The total force acting on the system will be:
Ftotal=Fe+W=100N+100N=200N
Step 5: Calculate the Total Mass of the Four Charges
The total mass of the four charges is:
mtotal=1kg+2kg+3kg+4kg=10kg
Step 6: Calculate the Acceleration of the Center of Mass
Using Newton's second law, we can find the acceleration (a) of the center of mass of the four charges:
a=Ftotalmtotal
Substituting the values:
a=200N10kg=20m/s2
Final Answer
The acceleration of the center of mass of the four charges immediately after the release is:
20m/s2
---
We have four point positive charges located at the vertices of a square and a fifth charge of mass 10 kg placed on the axis of the square. The four charges have masses of 1 kg, 2 kg, 3 kg, and 4 kg. The weight of the fifth charge is balanced by the electrostatic force due to the four charges.
The weight of the fifth charge (mass = 10 kg) can be calculated using the formula:
W=mg
Where g=10m/s2.
W=10kg×10m/s2=100N
Since the weight of the fifth charge is balanced by the electrostatic force (Fe) from the four charges, we have:
Fe=W=100N
When the four charges are released, they will experience a net force due to their mutual repulsion. The total force acting on the center of mass of the four charges can be considered as the sum of their individual forces. Since they are all positive charges, they will repel each other.
Ftotal=Fe+W=100N+100N=200N
The total mass of the four charges is:
mtotal=1kg+2kg+3kg+4kg=10kg
Using Newton's second law, we can find the acceleration (a) of the center of mass of the four charges:
a=Ftotalmtotal
Substituting the values:
a=200N10kg=20m/s2
The acceleration of the center of mass of the four charges immediately after the release is:
20m/s2
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective
32 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct
47 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises
58 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
Two point charges of same magnitude and opposite sign are fixed at point a and B. A third small point charge is to be balanced at point P by the electrostatic force due to these two charges. The point P :

View SolutionFour point charges are placed at the corners of a square ABCD of side 10 cm, as shown in figure. The force on a charge of 1μC placed at the centre of square is

View Solution
Knowledge Check
Four charges are arranged at the corners of a square ABCD, as shown in the adjoining figure. The force on the charge kept at the centre O is
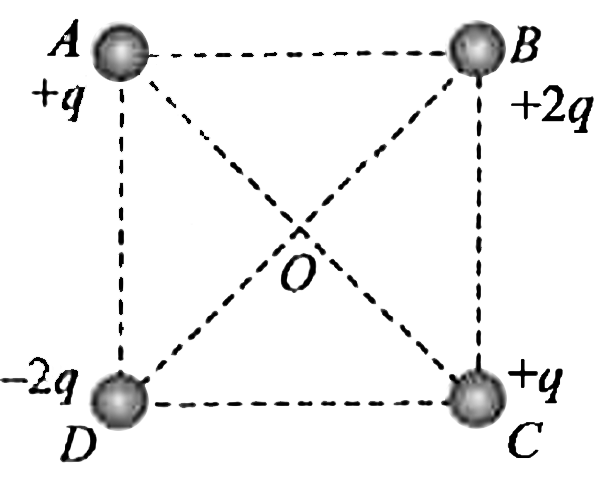 Aalong the diagonal BDBalong the diagonal ACCzeroDperpendicular to side AB
Aalong the diagonal BDBalong the diagonal ACCzeroDperpendicular to side AB
What is the amount of charge possessed by 1kg of electrons
View SolutionDoes the force on a charge due to another charge depend on the charges present nearby?
View SolutionDoes the force on a charge due to another charge depend on the charges present nearby?
View SolutionFour equal positive charge are fixed at the vertical of a square of side L. Z-axis is perpendicular to plane of the square. The point Z=0 is the point where the diagonals of the square intersect each other. The plot of electic field due to the charges, as one moves on the Z-axis is
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .
.
View SolutionFour pointed charges are placed on vertices of a square.If all the charges are brought to any one of the vertices.The change in potential at the centre of square due to this would be
View SolutionFour positive charges (2√2−1)Q are arranged at the four corners of a square. Another charge q is placed at the centre of the square. Resulting force acting on each corner charge is zero if q is
View Solution
