Consider two points 1and2 in a region outside a charged sphere. Two points are not very far away from the sphere. If EandV respresent the electric fileld vector and the electric potential. Which of the following is not possible ?
∣∣→E1∣∣=∣∣→E2∣∣,V1=V2
→E1≠→E2,V1≠V2
→E1≠→E2,V1=V2
∣∣→E1∣∣=∣∣→E1∣∣,V1≠V2
The correct Answer is:D
To solve the problem, we need to analyze the relationship between electric field (E) and electric potential (V) in the context of two points (1 and 2) outside a charged sphere.
1. Understanding Electric Field and Electric Potential:
- The electric field (E) at a point in space due to a charged object is a vector quantity that represents the force per unit charge experienced by a positive test charge placed at that point.
- The electric potential (V) at a point is a scalar quantity that represents the work done in bringing a unit positive charge from infinity to that point against the electric field.
2. Equipotential Surfaces:
- An equipotential surface is a surface where the electric potential is the same at every point. This means that if two points lie on the same equipotential surface, their potentials (V1 and V2) will be equal (V1 = V2).
- The electric field (E) is always perpendicular to the equipotential surfaces. Therefore, if two points are on the same equipotential surface, the electric field at those points can be equal (E1 = E2).
3. Analyzing the Given Options:
- Option 1: If E1 = E2, then V1 must equal V2 (both points are on the same equipotential surface). This is possible.
- Option 2: If E1 ≠ E2, it is possible for V1 to equal V2. This can occur if the points are at different distances from the charge but still have the same potential due to the nature of electric fields.
- Option 3: If E1 ≠ E2, it is also possible for V1 ≠ V2. This is straightforward as different electric fields generally correspond to different potentials.
- Option 4: If E1 = E2, then V1 cannot be different from V2. This is not possible because equal electric fields imply equal potentials if they are on the same equipotential surface.
4. Conclusion:
- The option that is not possible is Option 4: If E1 = E2, then V1 cannot be different from V2.
Final Answer:
The option that is not possible is Option 4.
---
- The electric field (E) at a point in space due to a charged object is a vector quantity that represents the force per unit charge experienced by a positive test charge placed at that point.
- The electric potential (V) at a point is a scalar quantity that represents the work done in bringing a unit positive charge from infinity to that point against the electric field.
- An equipotential surface is a surface where the electric potential is the same at every point. This means that if two points lie on the same equipotential surface, their potentials (V1 and V2) will be equal (V1 = V2).
- The electric field (E) is always perpendicular to the equipotential surfaces. Therefore, if two points are on the same equipotential surface, the electric field at those points can be equal (E1 = E2).
- Option 1: If E1 = E2, then V1 must equal V2 (both points are on the same equipotential surface). This is possible.
- Option 2: If E1 ≠ E2, it is possible for V1 to equal V2. This can occur if the points are at different distances from the charge but still have the same potential due to the nature of electric fields.
- Option 3: If E1 ≠ E2, it is also possible for V1 ≠ V2. This is straightforward as different electric fields generally correspond to different potentials.
- Option 4: If E1 = E2, then V1 cannot be different from V2. This is not possible because equal electric fields imply equal potentials if they are on the same equipotential surface.
- The option that is not possible is Option 4: If E1 = E2, then V1 cannot be different from V2.
The option that is not possible is Option 4.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.3
20 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.4
15 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.1
14 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
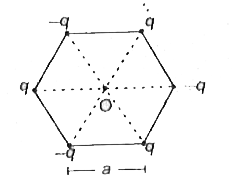
Six point charges are placed at the vertices of a regular hexagon of side a as shown. If E represents electric field and V represents electric potential at O then,
View SolutionTwo isolated charged conducting spheres of radii a and b produce the same electric field near their surface. The ratio of electric potentials on their surfaces is
View SolutionIn the figure shown a conducting sphere of inner radius 'a' and outer radius 'b' is given a charge Q. A point charge 'q' is placed in the cavity of this sphere at distance 'x'(<a) away from the centre. Find the electric field intensity and electric potentials at point P (outside the sphere) at distance r>b. Also find the electric potential at point C

View SolutionThe electric potential at a certain distance from a point charge is 600 V and the electric field is 200NC−1. Which of the following statements will be true?
View SolutionHow much work will be done in bringing a charge of 400μC from infinity to some point P in the region of electric field ? Given that the electric potential at point P is 20 V ?
View SolutionDraw a plot showing the variation of (i) electric field (E ) and (ii) electric potential (V) with distance r due to a point charge Q.
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View SolutionIf the potential at the centre of a uniformly charged hollow sphere of radius R is V, then electric field at a distance r from the centre of sphere will be (r>R).

View SolutionTwo spheres A and B of radius 'a' and 'b' respectively are at same electric potential. The ratio of the surface charge densities of A and B is
View SolutionConsider a sphere of radius R having charge q uniformly distributed insider it. At what minimum distance from surface the electric potential is half of the electric potential at its centre?
View Solution
