A uniform electric field exists in plane. The potential of points and are and 1 respectively. The electric field is
The correct Answer is:D
To find the electric field in the given problem, we need to analyze the potential at the given points and use the relationship between electric field and electric potential.
Step 1: Identify the points and their potentials
We have three points with their coordinates and potentials:
- Point A: A(−2m,2m) with potential VA=4V
- Point B: B(−2m,2m) with potential VB=16V
- Point C: C(2m,4m) with potential VC=12V
Step 2: Calculate the electric field in the x-direction
The electric field Ex can be calculated using the formula:
Ex=−ΔVΔx
where ΔV is the change in potential and Δx is the change in x-coordinate.
Using points A and B:
- Since both A and B have the same x-coordinate (-2 m), we can use points A and C for the calculation.
ΔV=VC−VA=12V−4V=8V
Δx=2m−(−2m)=4m
Thus,
Ex=−8V4m=−2V/m
Step 3: Calculate the electric field in the y-direction
Now, we calculate the electric field Ey using the same formula:
Ey=−ΔVΔy
Using points A and C:
ΔV=VC−VA=12V−4V=8V
Δy=4m−2m=2m
Thus,
Ey=−8V2m=−4V/m
Step 4: Combine the electric field components
The total electric field →E can be expressed as:
→E=Ex^i+Ey^j
Substituting the values we found:
→E=(−2^i)+(−4^j)=−2^i−4^j
Final Answer
The electric field is:
→E=−2^i−4^jV/m
We have three points with their coordinates and potentials:
- Point A: A(−2m,2m) with potential VA=4V
- Point B: B(−2m,2m) with potential VB=16V
- Point C: C(2m,4m) with potential VC=12V
The electric field Ex can be calculated using the formula:
Ex=−ΔVΔx
where ΔV is the change in potential and Δx is the change in x-coordinate.
- Since both A and B have the same x-coordinate (-2 m), we can use points A and C for the calculation.
Δx=2m−(−2m)=4m
Thus,
Ex=−8V4m=−2V/m
Now, we calculate the electric field Ey using the same formula:
Ey=−ΔVΔy
ΔV=VC−VA=12V−4V=8V
Δy=4m−2m=2m
Thus,
Ey=−8V2m=−4V/m
The total electric field →E can be expressed as:
→E=Ex^i+Ey^j
Substituting the values we found:
→E=(−2^i)+(−4^j)=−2^i−4^j
The electric field is:
→E=−2^i−4^jV/m
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.3
20 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.4
15 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.1
14 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
A uniform electric fied exists in x-y plane. The potential of ponts A(2m,2m),B(−2m,2m) and C(2m,3m) are 4V,16V and 12V respectively. The electric field is
View SolutionA uniform electric field is along x-axis. The potential difference VA−VB=10V is between two points A (2m, 3m) and (4m, 8m). Find the electric field intensity.
View SolutionA, B, C, D, P, and Q are points in a uniform electric field. The potentials at these points are V(A)=2V.V(P)=V(B)=V(D)=5V, and V(C)=8V. Find the electric field at P.
 .
.
View SolutionThe velocities of our molecules are V, 2V, 4V and √2V, respectively. Their r.m.s. speed is
View SolutionA uniform electric field of strength e exists in a region. An electron (charge -e, mass m) enters a point A with velocity Vˆj. It moves through the electric field & exits at point B. Then :
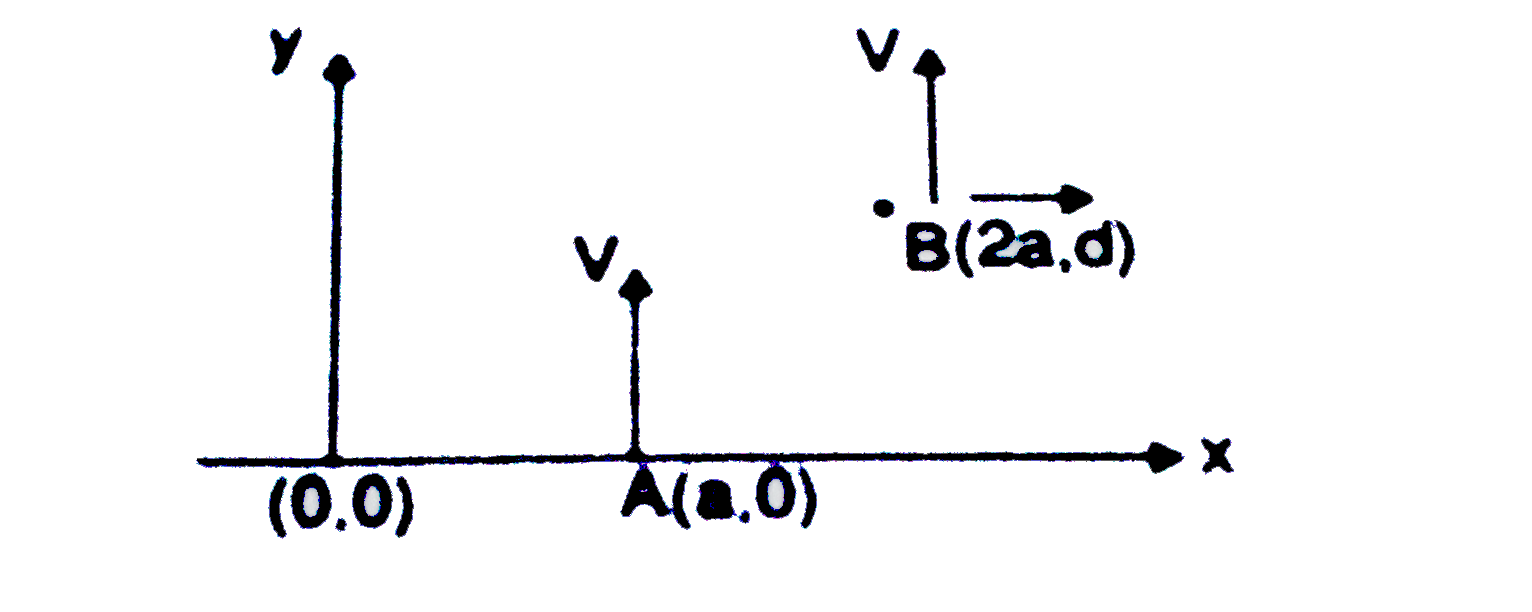
View SolutionThe electrode potentials for M2+(aq)+e−→M+(aq) and M+(aq)+e−→M(s) are 0.25 V and 0.60 V respectively.The value of E∘_M2+M is
View SolutionAn uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
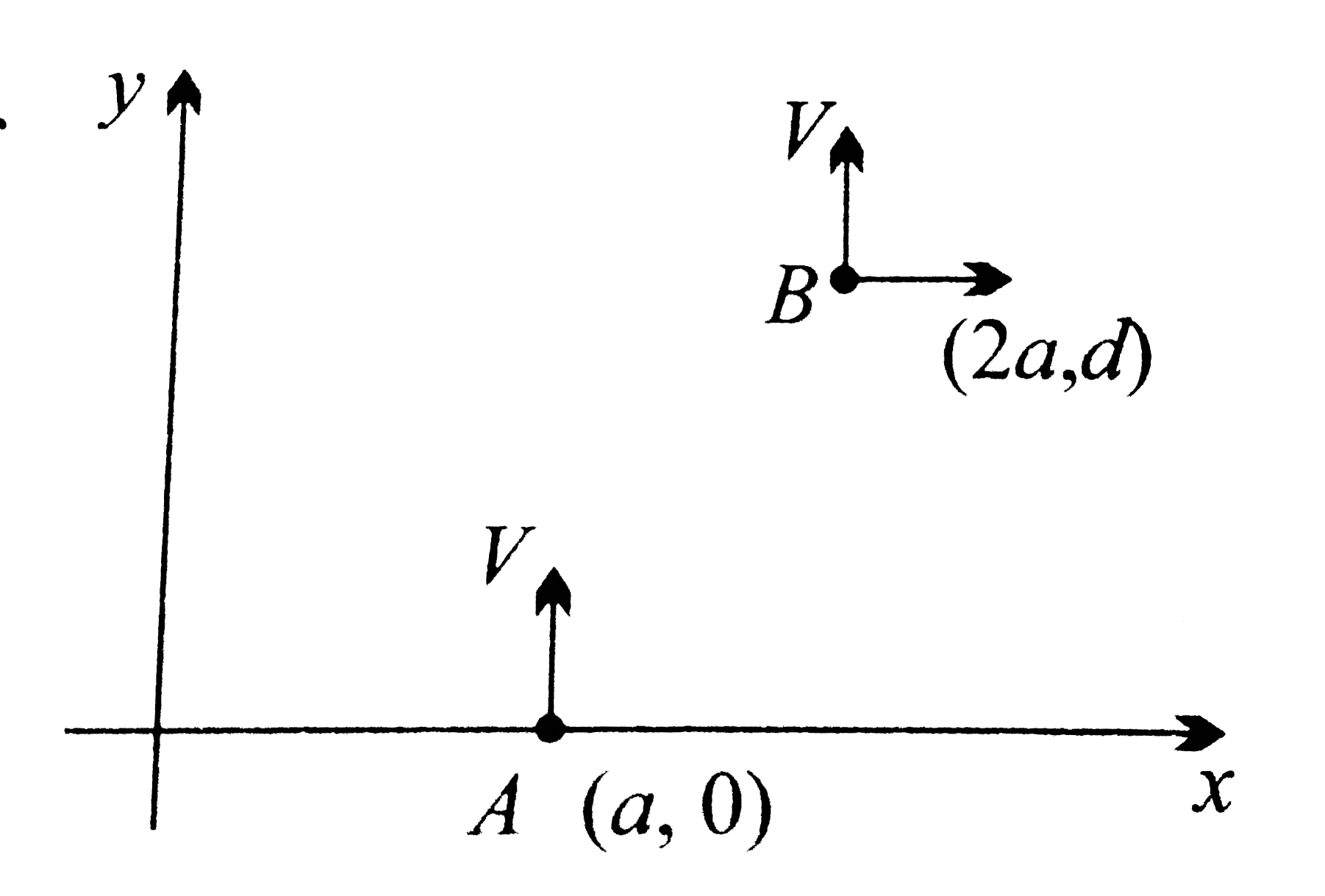 .
.
Find electric field.
View SolutionA uniform electric field of strength E exists in region. A electron enters a point A with velocity v as shown. It moves through the electric field and reaches at point B. Velocity particle at B is 2v at 30∘ with x-axis .
Then
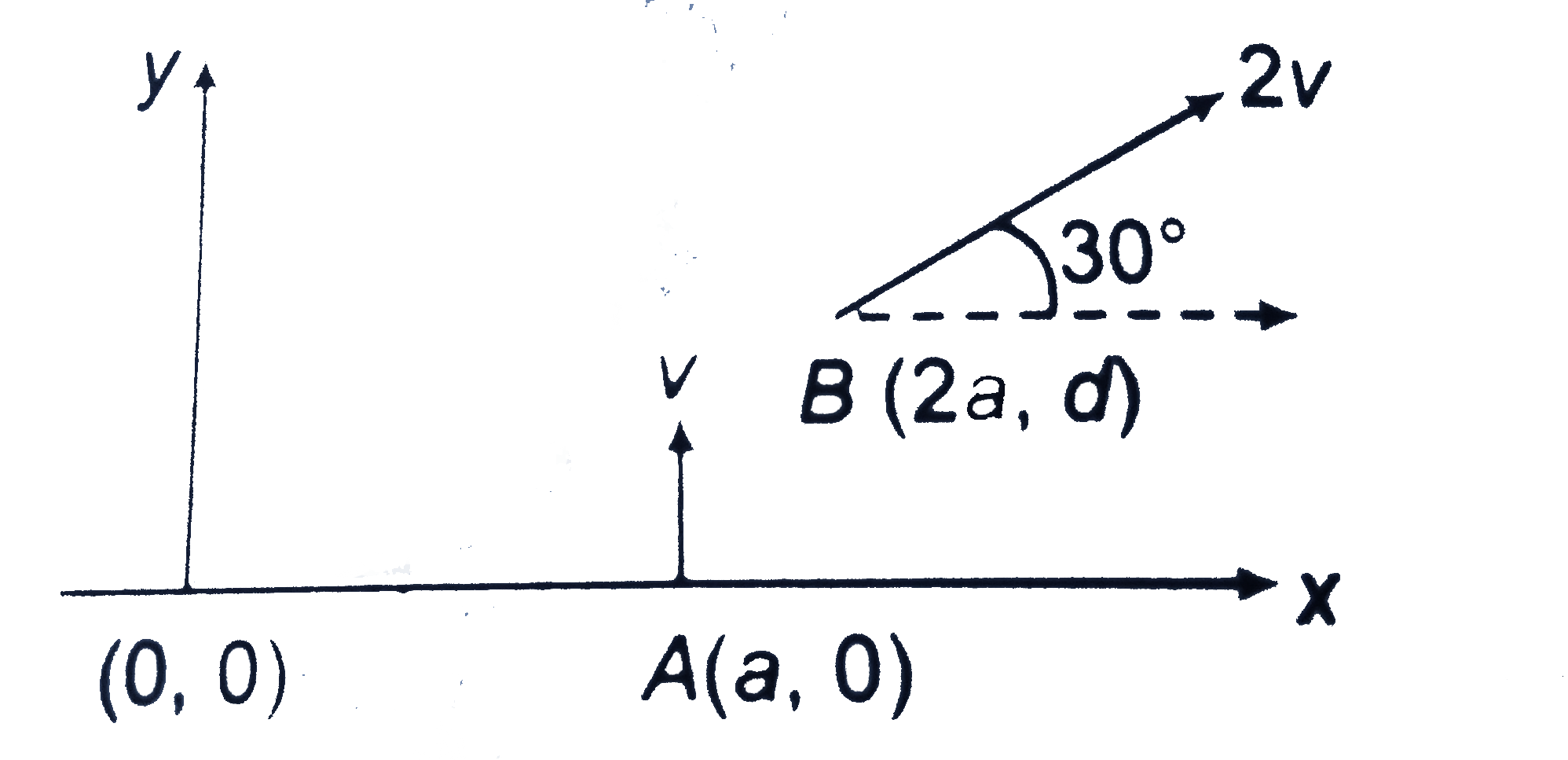
View SolutionFind the potential difference VAB between A(2m,1m,0) and B(0,2m,4m) in an electric field,
E=(xˆi−2yˆj+zˆk)Vm
View SolutionAn electric field →E=Bxˆi exists in space, where B=20V/m2. Taking the potential at (2m, 4m) to be zero, find the potential at the origin.
View Solution
