Four similar charges each of charge +q are placed at four corners of a square of side a. Find the value of integral −∫a/√2∞→E.→dr. (in volts) if value of integral −∫0a/√2→E.→dr=√2Kqa(whereK=14πε0)
4Kqa
3Kqa
3√2Kqa
4√2Kqa
The correct Answer is:C
To solve the problem, we need to calculate the integral of the electric field →E from infinity to a√2 and relate it to the given integral from a√2 to 0.
1. Understanding the Setup:
We have four charges +q located at the corners of a square with side length a. The electric field →E at any point in space due to these charges can be calculated using the principle of superposition.
2. Electric Potential Due to Charges:
The electric potential V at a point due to a point charge is given by:
V=K⋅qr
where K=14πϵ0 and r is the distance from the charge to the point.
3. Finding the Electric Field:
The electric field →E is related to the electric potential V by:
→E=−∇V
To find the electric field at a specific point, we can use the contributions from all four charges.
4. Setting Up the Integral:
We need to evaluate the integral:
−∫a√2∞→E⋅d→r
We can express this integral in terms of the known integral:
−∫0a√2→E⋅d→r=√2Kqa
5. Relating the Integrals:
We know from the properties of electric potential that:
V∞−Va√2=−∫a√2∞→E⋅d→r
and
Va√2−V0=−∫0a√2→E⋅d→r
Therefore, we can express the total change in potential from infinity to zero as:
V∞−V0=−∫0∞→E⋅d→r
6. Calculating the Final Value:
Since V0=0 (at the origin), we have:
V∞=−∫a√2∞→E⋅d→r+√2Kqa
Assuming V∞=0 (as we are at infinity), we can simplify:
0=−∫a√2∞→E⋅d→r+√2Kqa
Thus, we find:
−∫a√2∞→E⋅d→r=−√2Kqa
Final Answer:
The value of the integral −∫a√2∞→E⋅d→r is:
−√2Kqa
We have four charges +q located at the corners of a square with side length a. The electric field →E at any point in space due to these charges can be calculated using the principle of superposition.
The electric potential V at a point due to a point charge is given by:
V=K⋅qr
where K=14πϵ0 and r is the distance from the charge to the point.
The electric field →E is related to the electric potential V by:
→E=−∇V
To find the electric field at a specific point, we can use the contributions from all four charges.
We need to evaluate the integral:
−∫a√2∞→E⋅d→r
We can express this integral in terms of the known integral:
−∫0a√2→E⋅d→r=√2Kqa
We know from the properties of electric potential that:
V∞−Va√2=−∫a√2∞→E⋅d→r
and
Va√2−V0=−∫0a√2→E⋅d→r
Therefore, we can express the total change in potential from infinity to zero as:
V∞−V0=−∫0∞→E⋅d→r
Since V0=0 (at the origin), we have:
V∞=−∫a√2∞→E⋅d→r+√2Kqa
Assuming V∞=0 (as we are at infinity), we can simplify:
0=−∫a√2∞→E⋅d→r+√2Kqa
Thus, we find:
−∫a√2∞→E⋅d→r=−√2Kqa
The value of the integral −∫a√2∞→E⋅d→r is:
−√2Kqa
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.3
20 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.4
15 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.1
14 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
The value of the integral ∫π/2−π2√1+cos2x2dx is
View SolutionIf three point charges are placed at the three corners of a square of diagonals 2a as shown in figure. Then ∫AB→E.→dr will be -
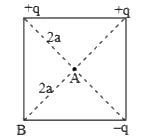
View SolutionThe value of the integral ∫a01x+√a2−x2dx, is
View SolutionThe value of the integral ∫π/2−π/2√cosx−cos2xdx is
View SolutionThe value of the integral
∫400π0√1−cos2xdx, is
View SolutionFour charges of same magnitude q are placed at four corners of a square of side a . The value electric potential at the centre of the souare will be (where k = 14πε0 )
View SolutionFor any n>1, evaluate the integral
∫∞01(x+√x2+1)ndx
View SolutionIf the value of the integral I=∫10dxx+√1−x2 is equal to πk, then the value of k is equal to
View SolutionIf the value of the integral ∫21ex2dx is α, then the value of ∫e4e√lnxdx is:
View SolutionFour positive charges (2√2−1)Q are arranged at the four corners of a square. Another charge q is placed at the centre of the square. Resulting force acting on each corner charge is zero if q is
View Solution
