A battery of 24 cells each of emf 1.5 V and internal resistnace 2Ω is to be connected in order to send the maximum current through a 12Ω resistor. The correct arrangement of cells will be
2 rows of 12 cells connected in parallel
3rows of 8 cells connected in parallel
4 rows of 6 cells connected in parallel
All of these
The correct Answer is:A
To solve the problem of connecting 24 cells, each with an emf of 1.5 V and an internal resistance of 2 Ω, to send the maximum current through a 12 Ω resistor, we can follow these steps:
Step 1: Understand the Configuration
We have 24 cells, each with an emf of 1.5 V and an internal resistance of 2 Ω. We need to determine how to connect these cells to maximize the current through a 12 Ω resistor.
Step 2: Define Variables
Let:
- n = number of cells in series in each row
- m = number of rows connected in parallel
Step 3: Calculate Total Emf and Internal Resistance
When cells are connected in series:
- The total emf of one row = n×1.5V
- The internal resistance of one row = n×2Ω
When rows are connected in parallel:
- The total emf remains the same as one row = n×1.5V
- The total internal resistance of m rows = n×2mΩ
Step 4: Apply the Condition for Maximum Current
For maximum current through the external resistor R (which is 12 Ω), the condition is:
R=nm×2
Thus,
12=nm×2
From this, we can derive:
n=6m (Equation 1)
Step 5: Use the Total Number of Cells
The total number of cells is given as 24:
n×m=24 (Equation 2)
Step 6: Substitute and Solve
Substituting Equation 1 into Equation 2:
6m×m=24
6m2=24
m2=4
m=2
Now substituting m back into Equation 1 to find n:
n=6×2=12
Step 7: Conclusion
Thus, we find that:
- Number of cells in series n=12
- Number of rows m=2
Therefore, the correct arrangement of cells is 2 rows of 12 cells connected in parallel.
We have 24 cells, each with an emf of 1.5 V and an internal resistance of 2 Ω. We need to determine how to connect these cells to maximize the current through a 12 Ω resistor.
Let:
- n = number of cells in series in each row
- m = number of rows connected in parallel
When cells are connected in series:
- The total emf of one row = n×1.5V
- The internal resistance of one row = n×2Ω
- The total emf remains the same as one row = n×1.5V
- The total internal resistance of m rows = n×2mΩ
For maximum current through the external resistor R (which is 12 Ω), the condition is:
R=nm×2
Thus,
12=nm×2
From this, we can derive:
n=6m (Equation 1)
The total number of cells is given as 24:
n×m=24 (Equation 2)
Substituting Equation 1 into Equation 2:
6m×m=24
6m2=24
m2=4
m=2
n=6×2=12
Thus, we find that:
- Number of cells in series n=12
- Number of rows m=2
Topper's Solved these Questions
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Combination of Resistance 2
14 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
Similar Questions
24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View Solution100 cells each of emf 5V and internal resistance 1Ω are to be arranged to produce maximum current in a 25Ω resistance. Each row contains equal number of cells. Find the number of rows.
View SolutionMaximum current produced by a cell of emf 10 V and internal resistance 2Ω is
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 6 Ω resistor.
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 3 Ω resistor,
View SolutionFind the current drawn from a cell of emf 2 V and internal resistance 2Ω connected to the network given below.
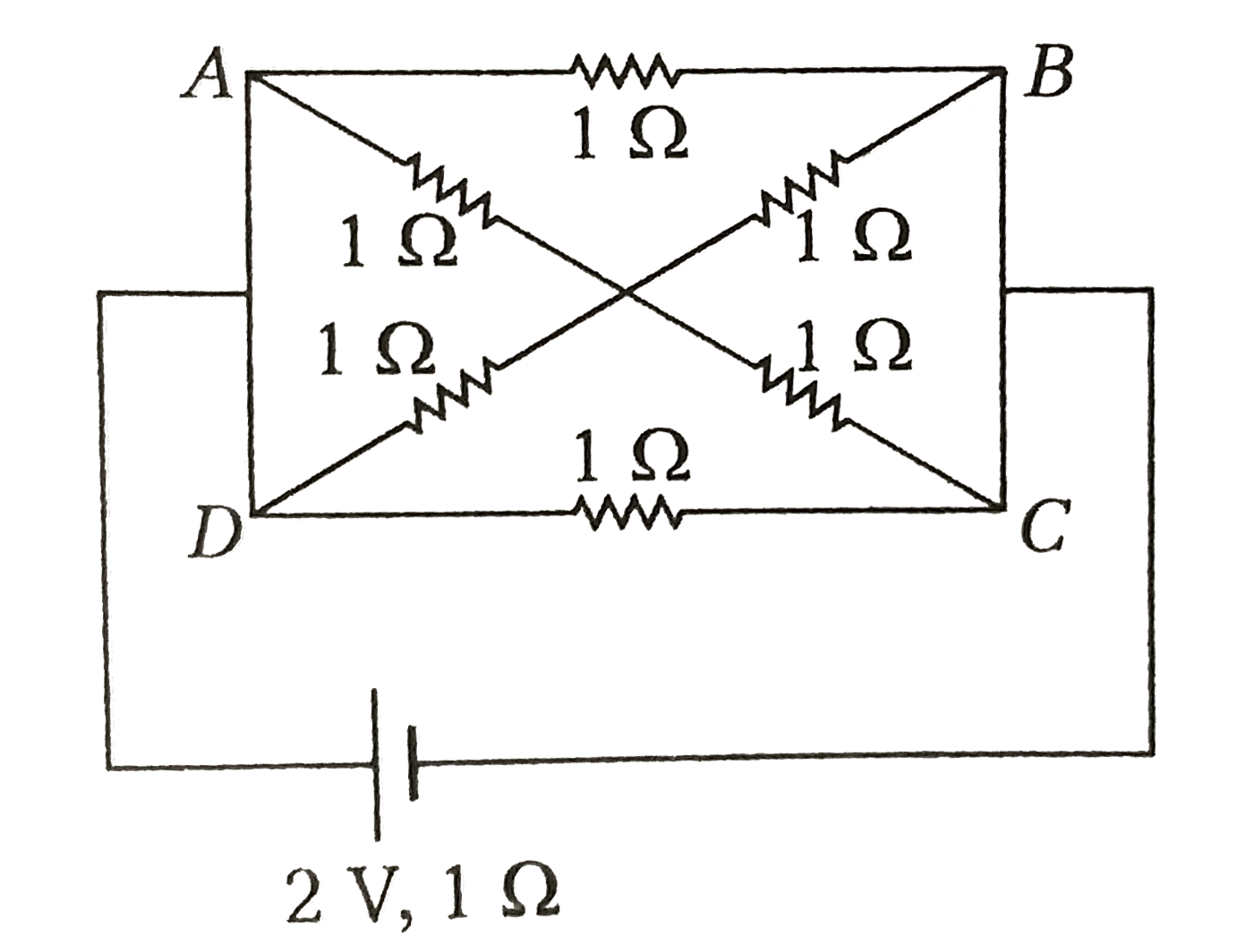
View Solution24 cells of emf 1.5V each having internal resistance of 1 ohm are connected to an external resistance of 1.5 ohms. To get maximum current,
View SolutionThree identical cells, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View SolutionEight cells marked 1 to 8, each of emf 5V and internal resistance 0.2Ω are connected as shown. What is the reading of ideal voltmeter ?
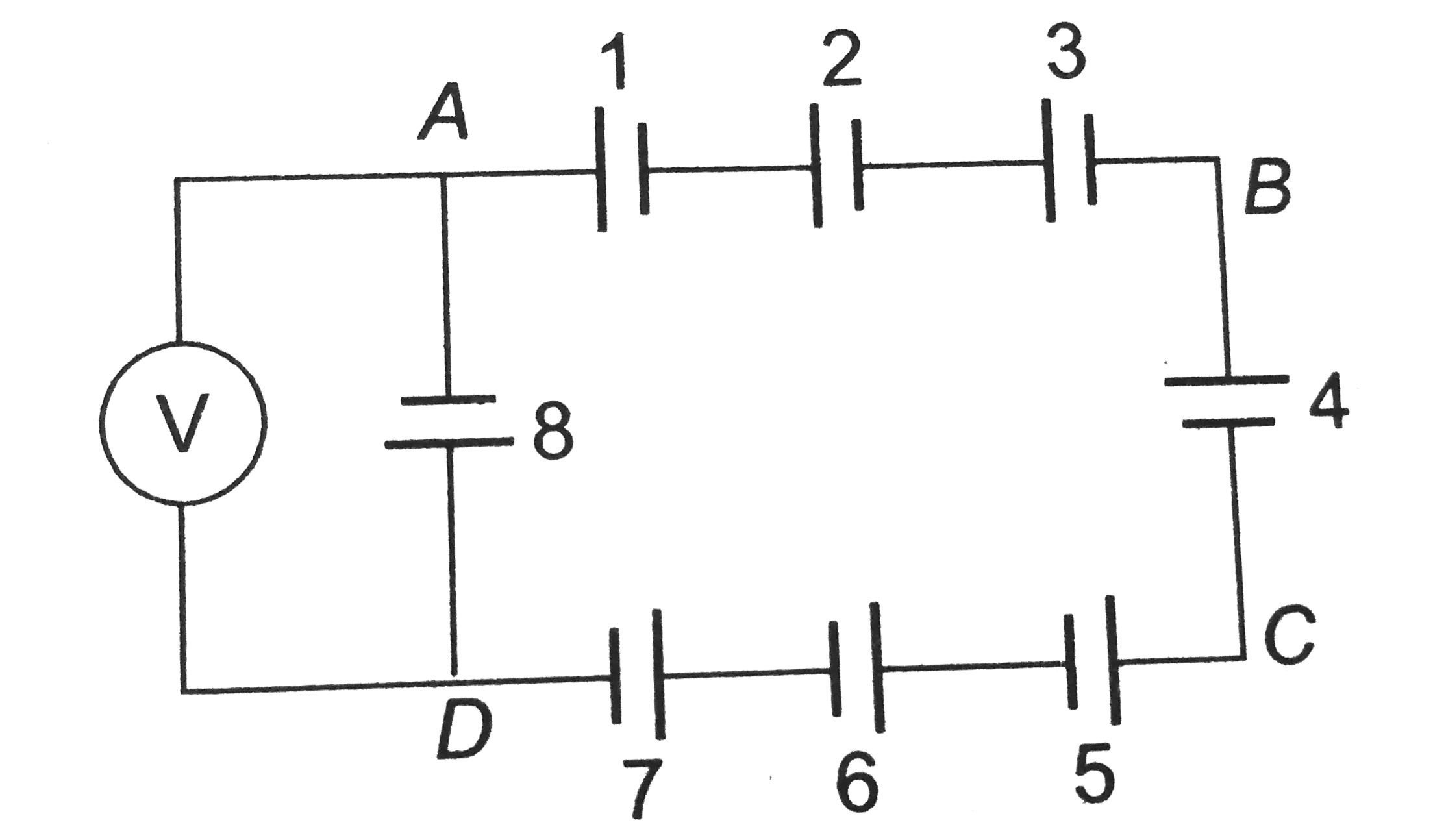
View Solution
