A battery of e.m.f. 10 V and internal resistance 2Ω is connected in primary circuit with a uniform potentiometer wire and a rheostat whose resistance is fixed at 998Ω.A battery of unknown e.m.f. is being balanced on this potentiometer wire and balancing length is found to be 50 cm.When area of cross section of potentiometer wire is doubled, then balancing length is found to be 75 cm.
(i)Calculate e.m.f. of the battery.
(ii)Calculate resistivity of potentiometer wire if length of wire is 100 cm and area of cross-section (initially) is 100cm2.
The correct Answer is:(a)2.5 volt , (b)10Ω−m
To solve the problem step by step, we will follow the outlined procedure:
Step 1: Understand the given data
- E.M.F. of the primary battery (E) = 10 V
- Internal resistance of the battery (r) = 2 Ω
- Fixed resistance of the rheostat (R) = 998 Ω
- Balancing length for the unknown battery (L1) = 50 cm = 0.5 m
- Balancing length when area of cross-section is doubled (L2) = 75 cm = 0.75 m
- Length of potentiometer wire (L) = 100 cm = 1 m
- Initial area of cross-section (A) = 100 cm² = 1 × 10⁻² m²
Step 2: Calculate the total resistance in the circuit
The total resistance in the primary circuit is given by:
Rtotal=R+r=998Ω+2Ω=1000Ω
Step 3: Calculate the potential difference across the potentiometer wire
Using Ohm's law, the potential difference (V) across the potentiometer wire can be calculated as:
V=E×RR+r
Substituting the values:
V=10V×998Ω1000Ω=9.98V
Step 4: Relate the balancing lengths to the E.M.F. of the unknown battery
The potential difference across the potentiometer wire is proportional to the balancing length:
EunknownV=LunknownL
Where L is the total length of the potentiometer wire.
For the first balancing length:
Eunknown=V×L1L=9.98V×0.5m1m=4.99V
Step 5: Calculate the new potential difference when the area is doubled
When the area is doubled, the resistance of the wire is halved. Thus, the new total resistance becomes:
Rnew=R2+r=998Ω2+2Ω=499Ω+2Ω=501Ω
The new potential difference across the potentiometer wire is:
Vnew=E×RnewRnew+r
Substituting the values:
Vnew=10V×501Ω503Ω≈9.95V
Using the new balancing length:
Eunknown=Vnew×L2L=9.95V×0.75m1m=7.4625V
Step 6: Calculate the resistivity of the potentiometer wire
Using the formula for resistivity:
ρ=R×AL
Where:
- R=1000Ω
- A=1×10−2m2
- L=1m
Substituting the values:
ρ=1000Ω×1×10−2m21m=10Ω⋅m
Final Answers:
(i) The E.M.F. of the unknown battery is approximately 4.99 V.
(ii) The resistivity of the potentiometer wire is 10 Ω·m.
- E.M.F. of the primary battery (E) = 10 V
- Internal resistance of the battery (r) = 2 Ω
- Fixed resistance of the rheostat (R) = 998 Ω
- Balancing length for the unknown battery (L1) = 50 cm = 0.5 m
- Balancing length when area of cross-section is doubled (L2) = 75 cm = 0.75 m
- Length of potentiometer wire (L) = 100 cm = 1 m
- Initial area of cross-section (A) = 100 cm² = 1 × 10⁻² m²
The total resistance in the primary circuit is given by:
Rtotal=R+r=998Ω+2Ω=1000Ω
Using Ohm's law, the potential difference (V) across the potentiometer wire can be calculated as:
V=E×RR+r
Substituting the values:
V=10V×998Ω1000Ω=9.98V
The potential difference across the potentiometer wire is proportional to the balancing length:
EunknownV=LunknownL
Where L is the total length of the potentiometer wire.
Eunknown=V×L1L=9.98V×0.5m1m=4.99V
When the area is doubled, the resistance of the wire is halved. Thus, the new total resistance becomes:
Rnew=R2+r=998Ω2+2Ω=499Ω+2Ω=501Ω
Vnew=E×RnewRnew+r
Substituting the values:
Vnew=10V×501Ω503Ω≈9.95V
Eunknown=Vnew×L2L=9.95V×0.75m1m=7.4625V
Using the formula for resistivity:
ρ=R×AL
Where:
- R=1000Ω
- A=1×10−2m2
- L=1m
ρ=1000Ω×1×10−2m21m=10Ω⋅m
(i) The E.M.F. of the unknown battery is approximately 4.99 V.
Topper's Solved these Questions
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Single Correct
94 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Multiple Correct
7 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Exercise 6.1
15 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - compression type
7 Videos
Similar Questions
If the resistance of potentiometer wire is 15r then calculate the balance length l
View SolutionThe length of the potentiometer wire is 600 cm and a current of 40 mA is flowing in it. When a cell of emf 2 V and internal resistance 10Ω is balanced on this potentiometer the balance length is found to be 500 cm. The resistance of potentiometer wire will be
View SolutionThere is a potentiometer wire of length 1200 cm and 60 mA current is flowing in it. A battery of emf 5V and internal resistance of 20ohm is balanced on potentiometer wire with balancing length 1000 cm. The resistance of potentiometer wire is
View SolutionA battery of unknown emf connected to a potentiometer has balancing length 560 cm. If a resistor of resistance 10 ohm, is connected in parallel with the cell the balancing length change by 60 cm. If the internal resistance of the cell is n10 ohm, the value of 'n' is
View SolutionA potentiometer wire of length 1m and resistance 20Ω is connected in series with a 15V battery and an external resistance 40Ω . A secondary cell of emf E in the secondary circuit is balanced by 24 cm long potentiometer wire. The emf E of the cell is ,
View SolutionAn ideal battery of emf 2 V and a series resistance R are connected in the primary circuit of a potentiometer of length 1 m and resistance 5Ω The value of R, to give a potential difference of 5 m V across 10 cm of potentiometer wire is
View SolutionAB is a potentiometer wire of length 100cm and its resistance is 10ohm. It is connected in series with a resistance R=40 ohm and a battery of e.m.f. wV and negigible internal resistance. If a source of unknown e.m.f. E is balanced by 40cm length of the potentiometer wire, the value of E is:

View SolutionAB is a potentiometer wire of length 100 cm and its resistance is 10Ω. It is connected in series with a resistance R = 40 Ω and a battery of emf 2 V and negligible internal resistance. If a source of unknown emf E is balanced by 40 cm length of the potentiometer wire, the value of E is
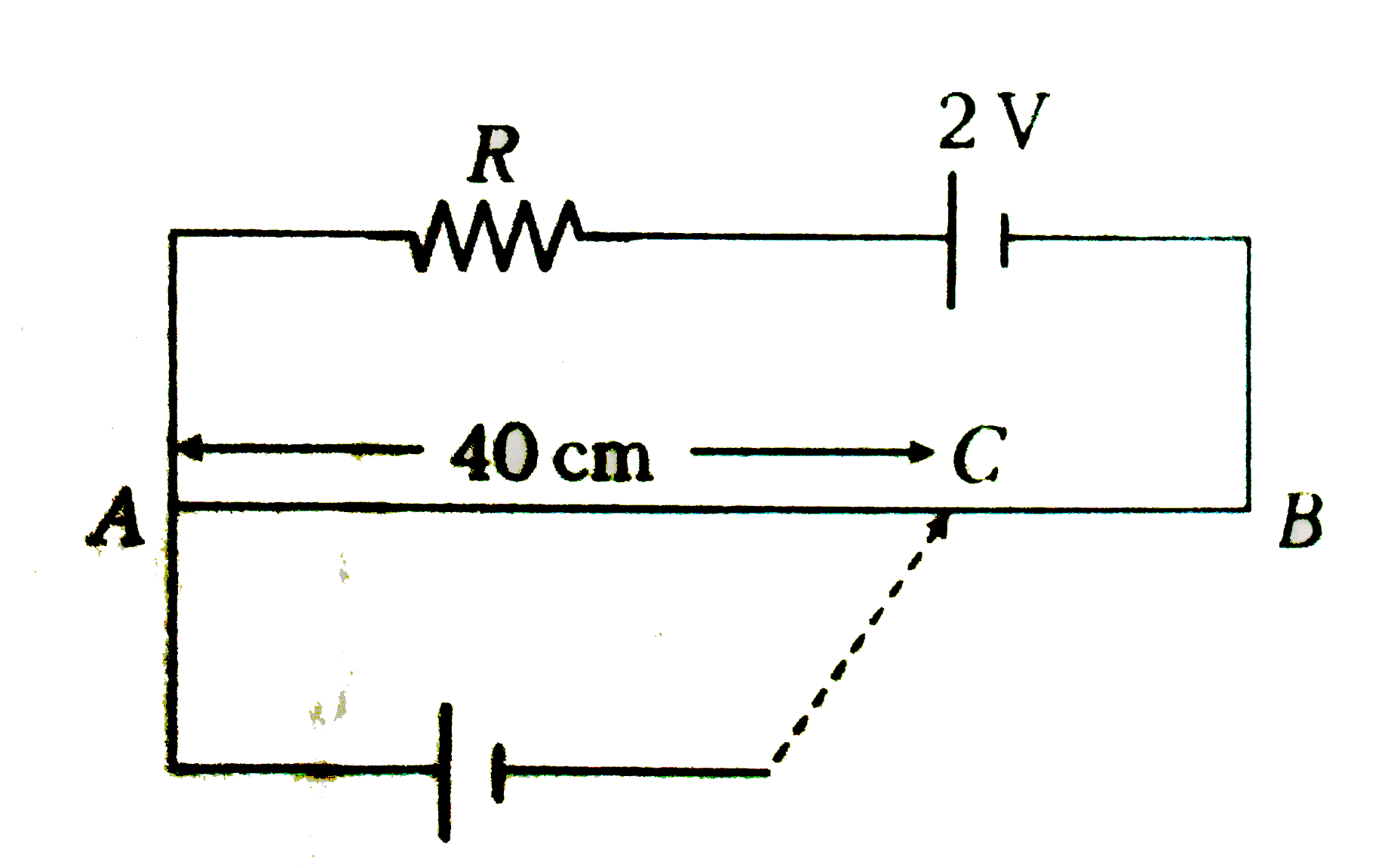
View SolutionAN ideal battery of 4 V and resistance R are connected in series in the primary circuit of a potentiometer of length 1 m and and resistance 5Ω the value of R, to give a difference of 56mV across 10 cm of potentiometer wire , is :
View SolutionIn a potentiometer experiment the balancing length with a cell is 560 cm. When an external resistance of 10Ω is connected in parallel to the cell, the balancing length changes by 60 cm. Find the internal resistance of the cell.
View Solution
