Question

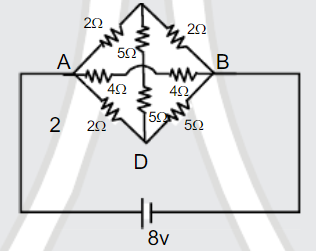
In Wheatstone's bridge $P=9ohm$, Q = 11 ohm$,R=4ohm$ and $S=6ohm$. How much resistance must be put in parallel to the resistance $S$ to balance the bridge

Options

A. `24 Omega`
B. `44/ 9 Omega`
C. `26.4 Omega`
D. `18.4 Omega`

Answer

C

Explanation

To solve the problem of finding the resistance that must be put in parallel to the resistance $$S$$ in a Wheatstone bridge to achieve balance, we can follow these steps:

1. Understand the Wheatstone Bridge Condition:
For a Wheatstone bridge to be balanced, the following condition must hold:
\( \frac{P}{Q} = \frac{R}{S'} \)
where \( S' \) is the equivalent resistance of \( S \) when a resistance \( R' \) is connected in parallel with it.

2. Identify Given Values:
From the problem, we have:
- \( P = 9 \, \Omega \)
- \( Q = 11 \, \Omega \)
- \( R = 4 \, \Omega \)
- \( S = 6 \, \Omega \)

3. Express the Equivalent Resistance \( S' \):
When a resistance \( R' \) is connected in parallel with \( S \), the equivalent resistance \( S' \) can be expressed as:
\( \frac{1}{S'} = \frac{1}{S} + \frac{1}{R'} \)
Rearranging gives:
\( S' = \frac{S \cdot R'}{S + R'} \)

4. Substitute for \( S' \):
From the balance condition:
\( \frac{P}{Q} = \frac{R}{S'} \)
We can substitute \( S' \):
\( \frac{9}{11} = \frac{4}{\frac{6 \cdot R'}{6 + R'}} \)

5. Cross Multiply and Solve for \( R' \):
Cross multiplying gives:
\( 9 \cdot \frac{6 \cdot R'}{6 + R'} = 44 \)
Simplifying this:
\( 54R' = 44(6 + R') \)
Expanding:
\( 54R' = 264 + 44R' \)
Rearranging terms:
\( 54R' - 44R' = 264 \)
\( 10R' = 264 \)
Dividing by 10:
\( R' = 26.4 \, \Omega \)

Final Answer:
The resistance that must be put in parallel with the resistance \( S \) to balance the bridge is \( R' = 26.4 \, \Omega \).