A resistor dissipates the power when connected to a certain generator. If the resistor is put in series with , the power dissipated by
decreases
increases
remains the same
any of the above depending upon the relative values of and
The correct Answer is:A
To solve the problem, we need to analyze the power dissipated by resistor R1 when it is connected to a generator and then when a second resistor R2 is added in series with it.
1. Initial Condition with Resistor R1:
- When only resistor R1 is connected to the generator, the power P dissipated by R1 can be expressed using the formula:
P=I2R1
- Here, I is the current flowing through R1.
2. Current Calculation:
- The current I can be calculated using Ohm's law, where V is the voltage provided by the generator:
I=VR1
- Substituting this into the power formula gives:
P=(VR1)2R1=V2R1
3. Adding Resistor R2 in Series:
- When resistor R2 is added in series with R1, the total resistance Rtotal becomes:
Rtotal=R1+R2
- The new current I′ flowing through the circuit is now:
I′=VR1+R2
4. Power Dissipated by R1 with R2 in Series:
- The power P′ dissipated by R1 when R2 is in series can be expressed as:
P′=(I′)2R1
- Substituting I′ into the power formula gives:
P′=(VR1+R2)2R1=V2R1(R1+R2)2
5. Comparison of Powers:
- To compare P′ and P:
P′=V2R1(R1+R2)2andP=V2R1
- Since R1+R2>R1, it follows that (R1+R2)2>R21. Therefore:
P′<P
- This means the power dissipated by R1 decreases when R2 is added in series.
Conclusion:
The power dissipated by resistor R1 decreases when resistor R2 is added in series.
Final Answer:
The power dissipated by R1 decreases.
- When only resistor R1 is connected to the generator, the power P dissipated by R1 can be expressed using the formula:
P=I2R1
- Here, I is the current flowing through R1.
- The current I can be calculated using Ohm's law, where V is the voltage provided by the generator:
I=VR1
- Substituting this into the power formula gives:
P=(VR1)2R1=V2R1
- When resistor R2 is added in series with R1, the total resistance Rtotal becomes:
Rtotal=R1+R2
- The new current I′ flowing through the circuit is now:
I′=VR1+R2
- The power P′ dissipated by R1 when R2 is in series can be expressed as:
P′=(I′)2R1
- Substituting I′ into the power formula gives:
P′=(VR1+R2)2R1=V2R1(R1+R2)2
- To compare P′ and P:
P′=V2R1(R1+R2)2andP=V2R1
- Since R1+R2>R1, it follows that (R1+R2)2>R21. Therefore:
P′<P
- This means the power dissipated by R1 decreases when R2 is added in series.
The power dissipated by resistor R1 decreases when resistor R2 is added in series.
The power dissipated by R1 decreases.
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Integer
5 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type
4 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
Similar Questions
A resistor R1 consumes electrical power P1 when connected to an emfε. When resistor R2 is connected to the same emf , it consumes electrical power P2 . In terms of P1andP2, what is the total electrical power consumed when they are both connected to this emf source
(a) in parallel
(b) in series
View SolutionA resistor R1 consumes electrical power P1 when connected to an emfε. When resistor R2 is connected to the same emf , it consumes electrical power P2 . In terms of P1andP2, what is the total electrical power consumed when they are both connected to this emf source
(a) in parallel
(b) in series
View SolutionA resistance R1 is connected to a source of constant voltage . On connecting a resistance R2 in series with R1
View SolutionA resistor of resistance R is connected to an ideal battery. If the value of R is decreased,the power dissipated in the resistor will
View SolutionA resistor of resistance R is connected to an ideal battery. If the value of R is decreased,the power dissipated in the resistor will
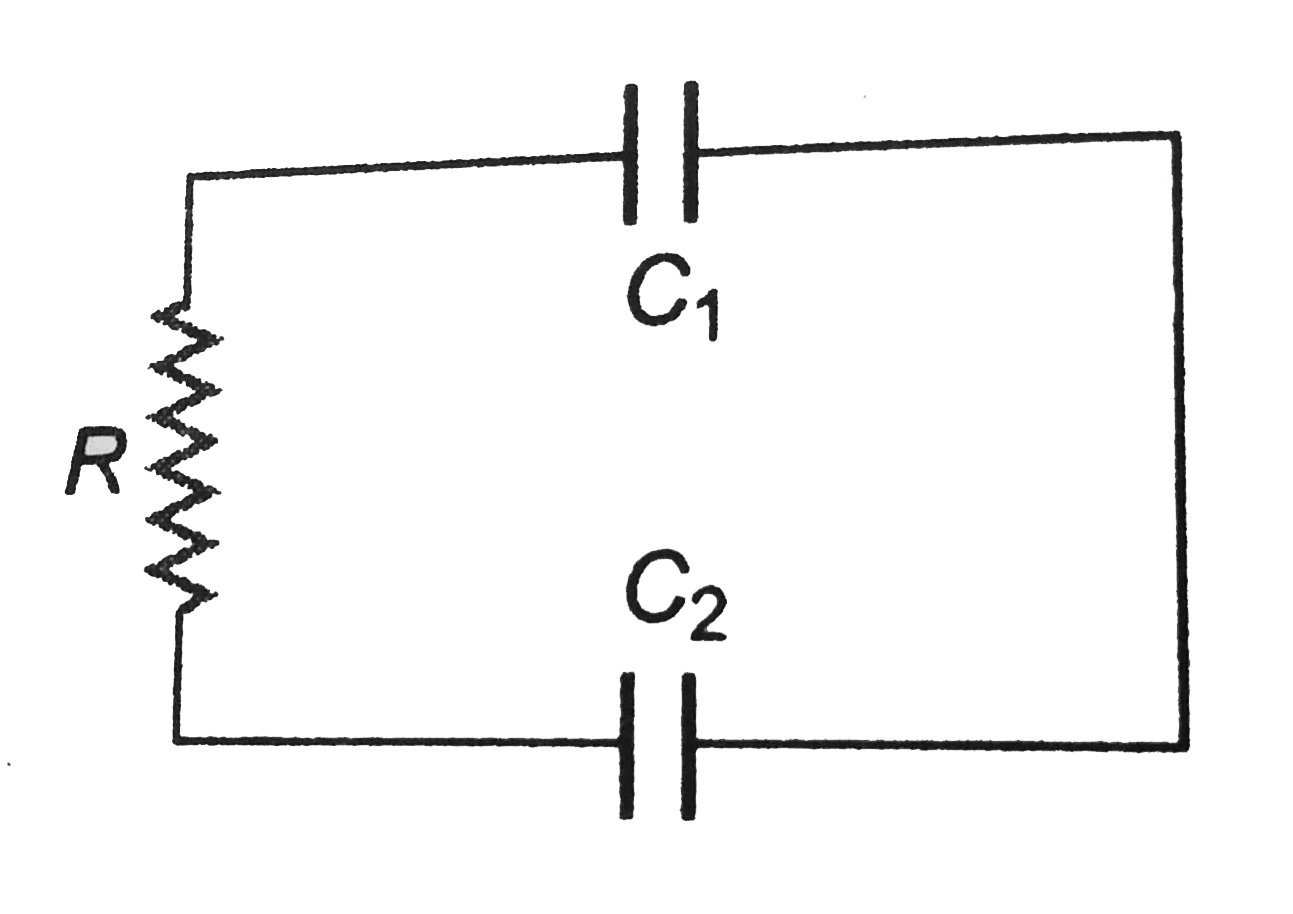
View SolutionA capacitors C1 is charged to a potential V and connected to another capacitor in seris with a resistor R as shown. It is observed that heat H1 is dissipated across resistance R, tilll the circuit reaches steady state. Same process is repeated using resistance of 2R. If H2 is heat dissipated in this case then
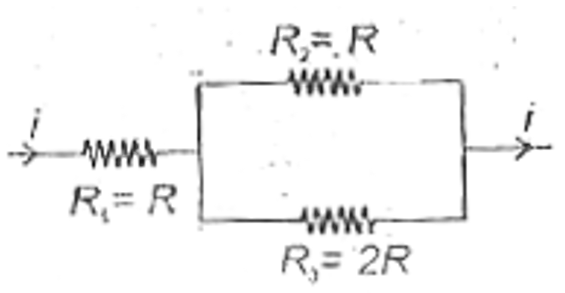
View SolutionIn the circuti shown ,the thermal power dissipated in R1 is P. The thermal power dissipated in R2 is .
View Solution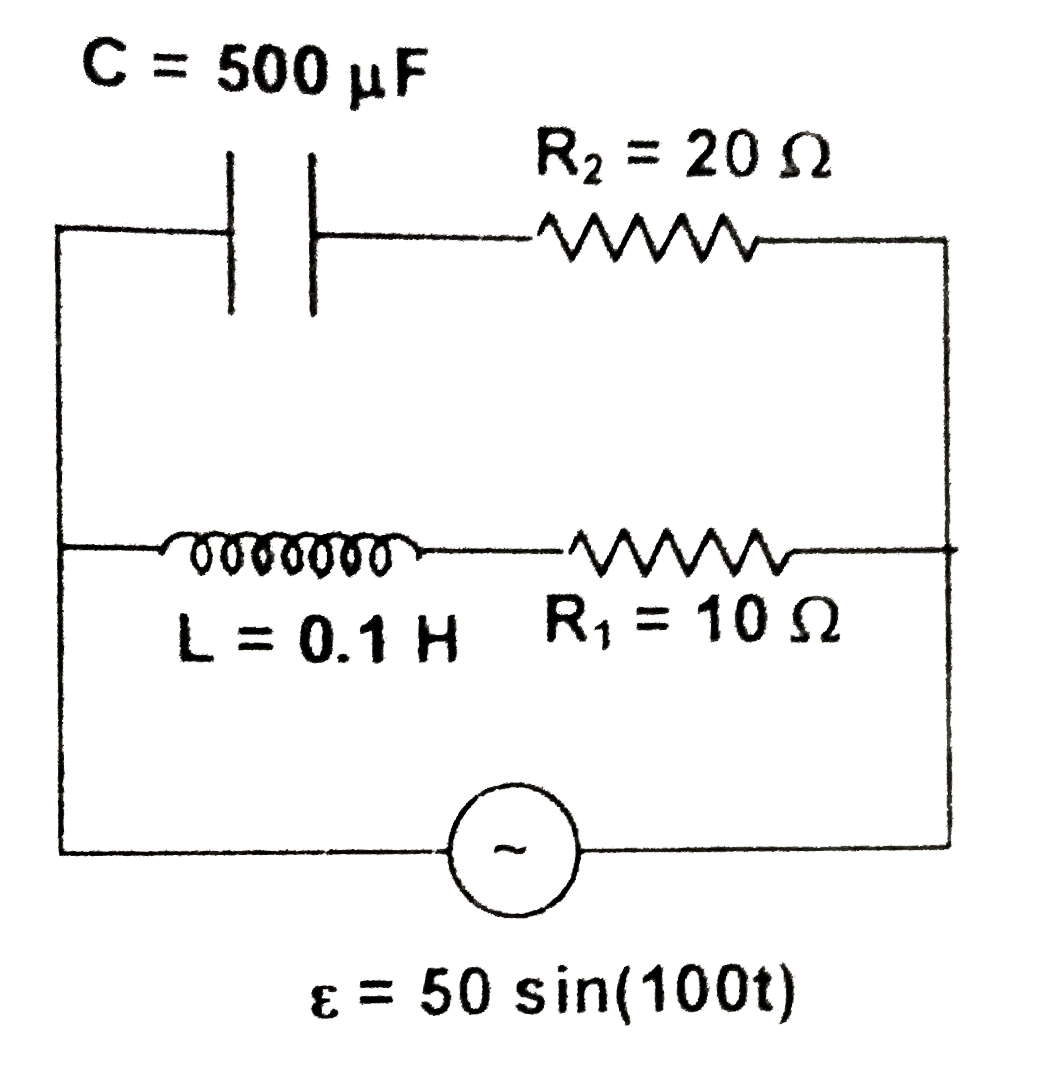
In the circuit shown the average power developed in the resistor R1 is
View SolutionA sinusoidal ac current flows through a resistor of resistance R . If the peak current is Ip , then the power dissipated is
View SolutionA sinusoidal ac current flows through a resistor of resistance R . If the peak current is Ip , then the power dissipated is
View Solution
