The equation of a trevelling wave In a uniform string of mass per unit length unit length is given as .Find the total energy transferred through the origin in time interval from t = 0 to (You can use the formula in instantaneous power if you know)
The correct Answer is:
To solve the problem, we need to find the total energy transferred through the origin in the time interval from t=0 to t=π12ω for the traveling wave described by the equation y=Asin(ωt−kx).
1. Identify the Wave Equation:
The wave equation is given as:
y=Asin(ωt−kx)
Here, A is the amplitude, ω is the angular frequency, and k is the wave number.
2. Calculate the Velocity of the Wave:
The velocity v of the wave can be derived from the wave equation. The velocity of a wave on a string is given by:
v=∂y∂t=Aωcos(ωt−kx)
3. Determine the Instantaneous Power:
The instantaneous power P transmitted by the wave is given by:
P=12μvω2
Substituting v into the power equation:
P=12μ(Aωcos(ωt−kx))ω2=12μAω3cos(ωt−kx)
4. Calculate Total Energy Transferred:
The total energy E transferred through the origin from t=0 to t=π12ω can be calculated by integrating the power over time:
E=∫π12ω0Pdt=∫π12ω012μAω3cos(ωt−kx)dt
5. Evaluate the Integral:
The integral can be evaluated as follows:
E=12μAω3∫π12ω0cos(ωt−kx)dt
The integral of cos can be computed:
∫cos(ωt−kx)dt=1ωsin(ωt−kx)
Thus,
E=12μAω3(1ωsin(ωt−kx))π12ω0
6. Substituting the Limits:
Evaluating the limits:
E=12μAω3(1ω(sin(π12−kx)−sin(−kx)))
Simplifying gives:
E=12μAω2(sin(π12−kx)+sin(kx))
Final Answer:
The total energy transferred through the origin in the time interval from t=0 to t=π12ω is:
E=12μAω2(sin(π12−kx)+sin(kx))
The wave equation is given as:
y=Asin(ωt−kx)
Here, A is the amplitude, ω is the angular frequency, and k is the wave number.
The velocity v of the wave can be derived from the wave equation. The velocity of a wave on a string is given by:
v=∂y∂t=Aωcos(ωt−kx)
The instantaneous power P transmitted by the wave is given by:
P=12μvω2
Substituting v into the power equation:
P=12μ(Aωcos(ωt−kx))ω2=12μAω3cos(ωt−kx)
The total energy E transferred through the origin from t=0 to t=π12ω can be calculated by integrating the power over time:
E=∫π12ω0Pdt=∫π12ω012μAω3cos(ωt−kx)dt
The integral can be evaluated as follows:
E=12μAω3∫π12ω0cos(ωt−kx)dt
The integral of cos can be computed:
∫cos(ωt−kx)dt=1ωsin(ωt−kx)
Thus,
E=12μAω3(1ωsin(ωt−kx))π12ω0
Evaluating the limits:
E=12μAω3(1ω(sin(π12−kx)−sin(−kx)))
Simplifying gives:
E=12μAω2(sin(π12−kx)+sin(kx))
The total energy transferred through the origin in the time interval from t=0 to t=π12ω is:
E=12μAω2(sin(π12−kx)+sin(kx))
Similar Questions
The figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.

Determine the tension in the string.View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
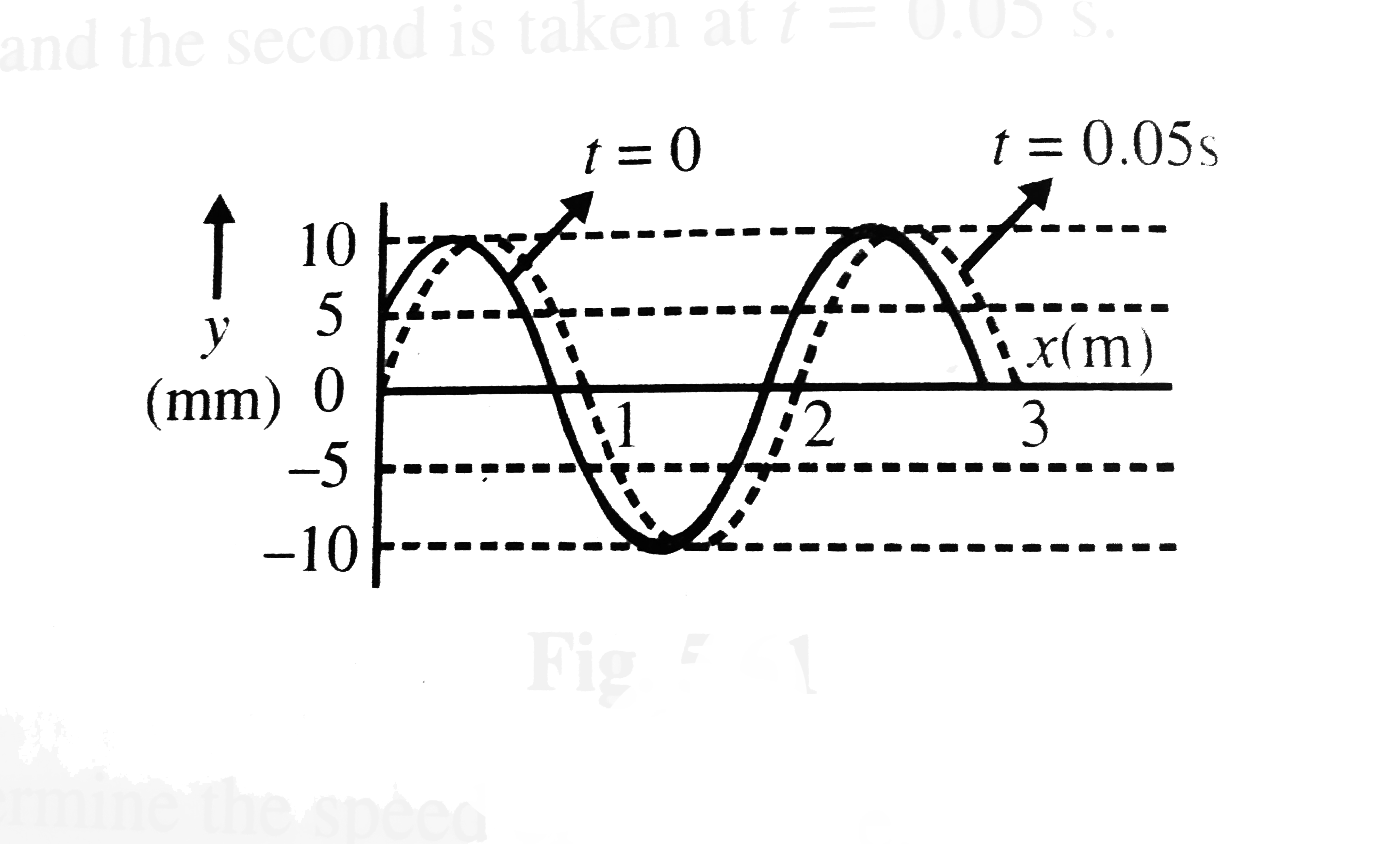
Determine the equation of the wave.View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
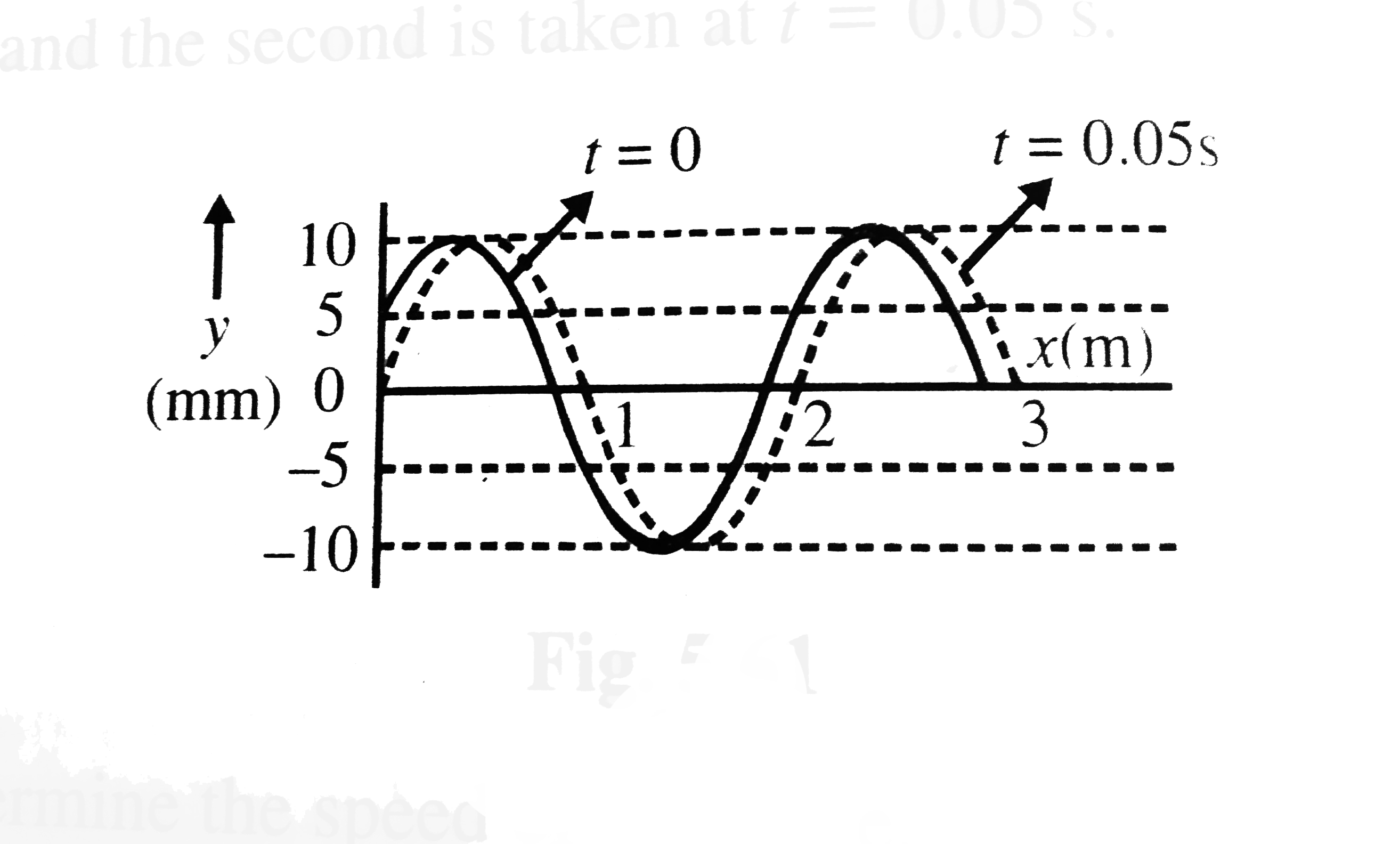
Determine the equation of the wave.View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
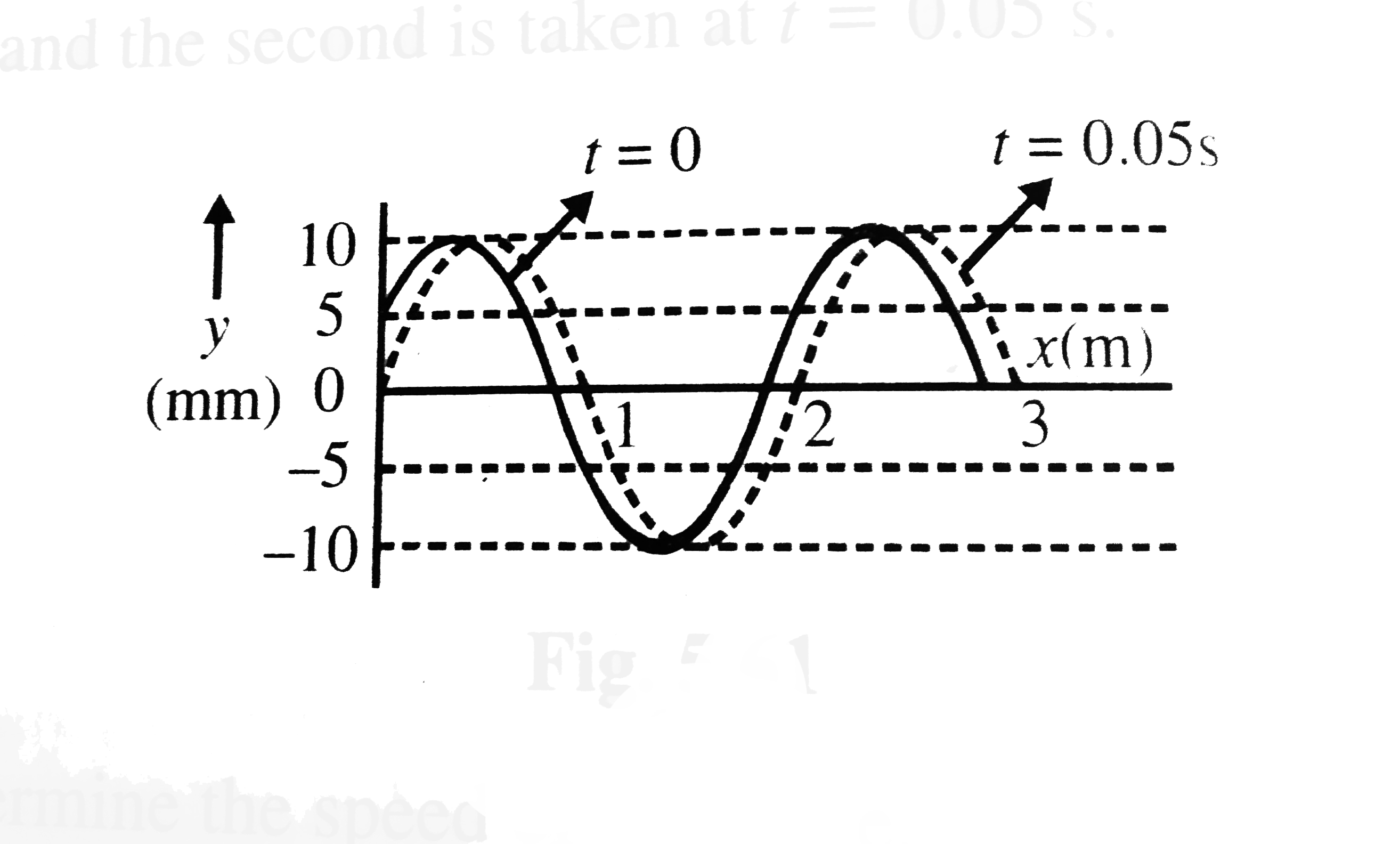
Determine the frequency of the wave.View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
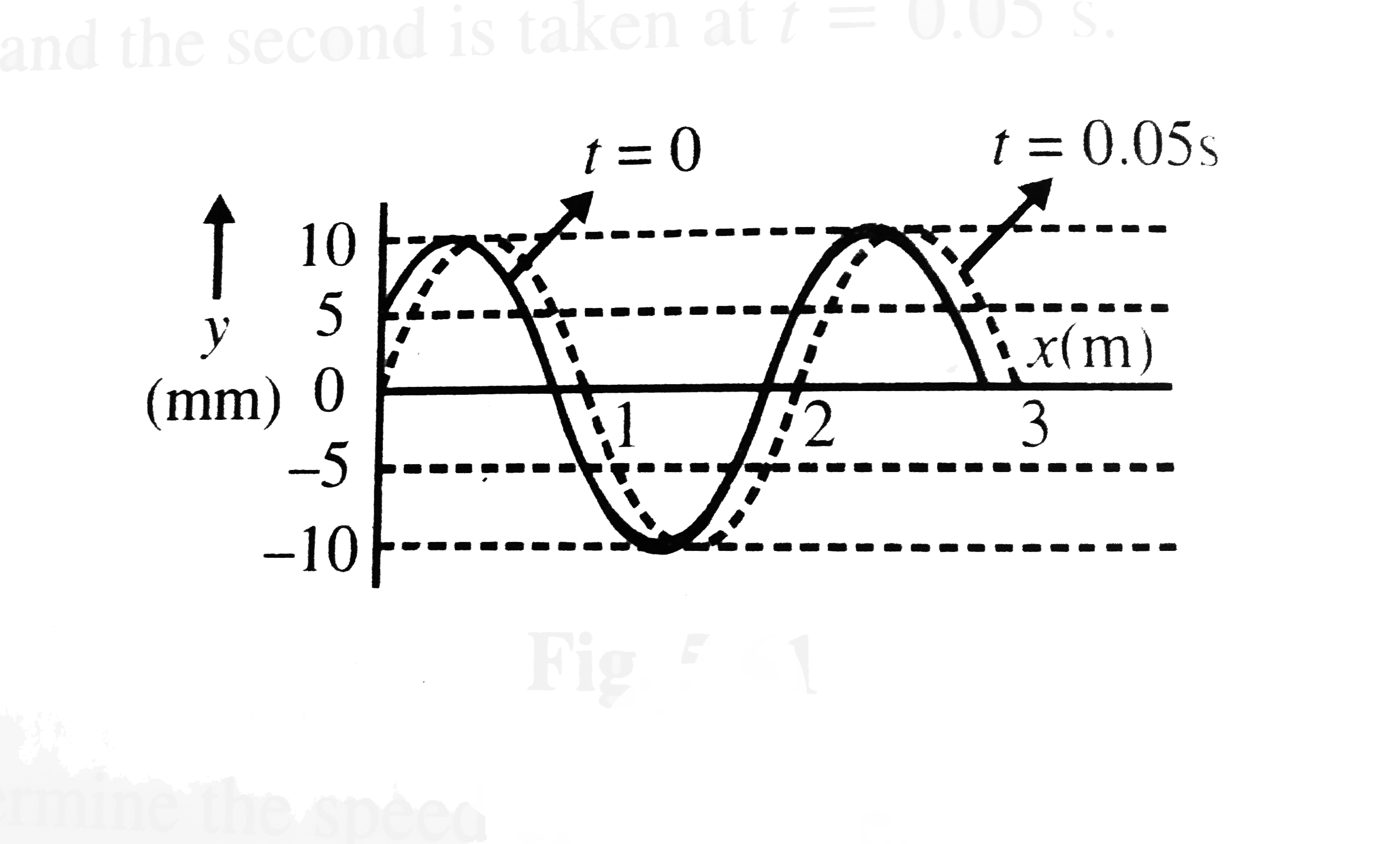
Determine the speed of the wave.View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
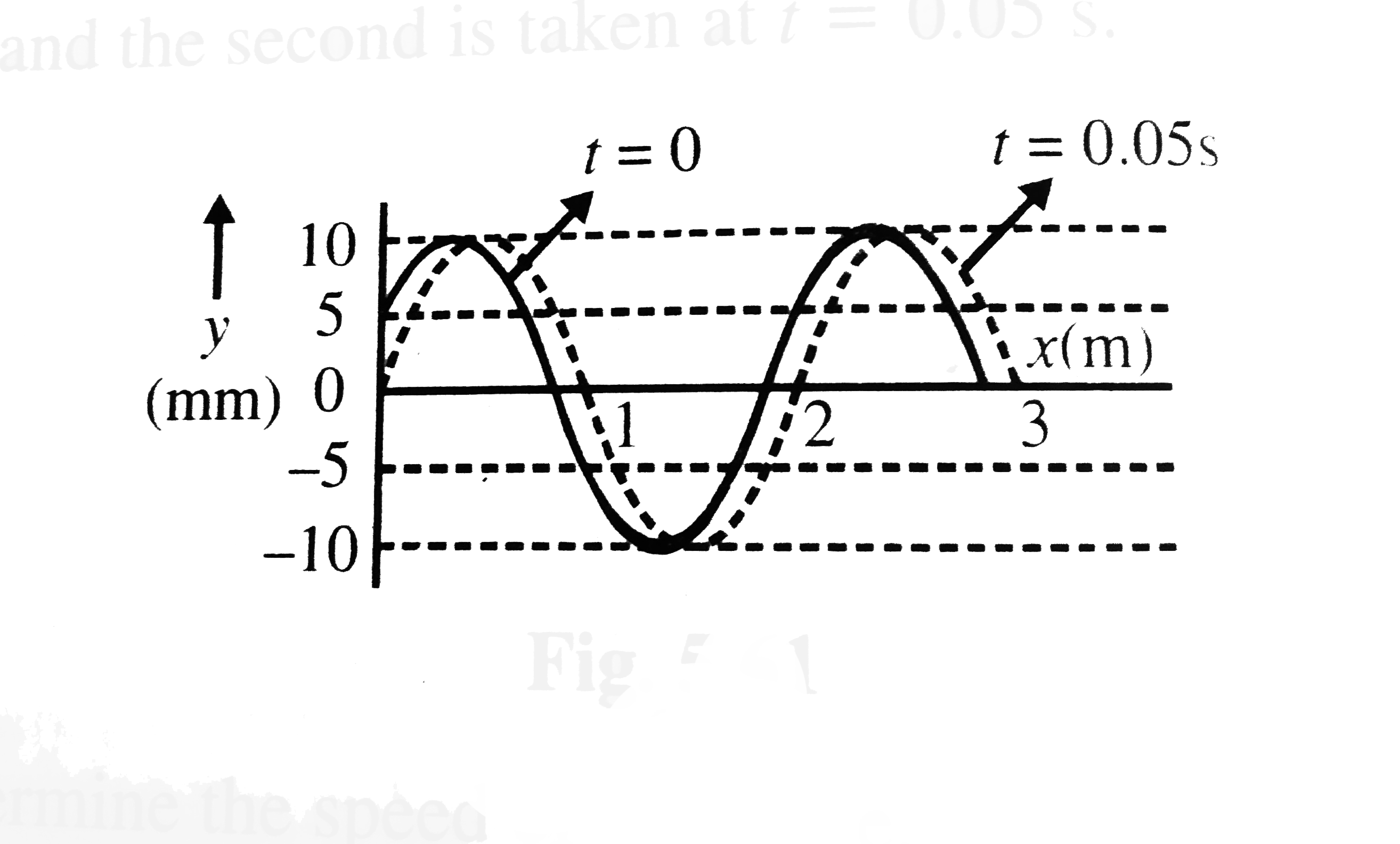
Determine the maximum speed of the particle.View SolutionA string tied between x=0andx=l vibrates in fundamental mode. The amplitude A, tension T and mass per unit length μ is given. Find the total energy of the string.
 View Solution
View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
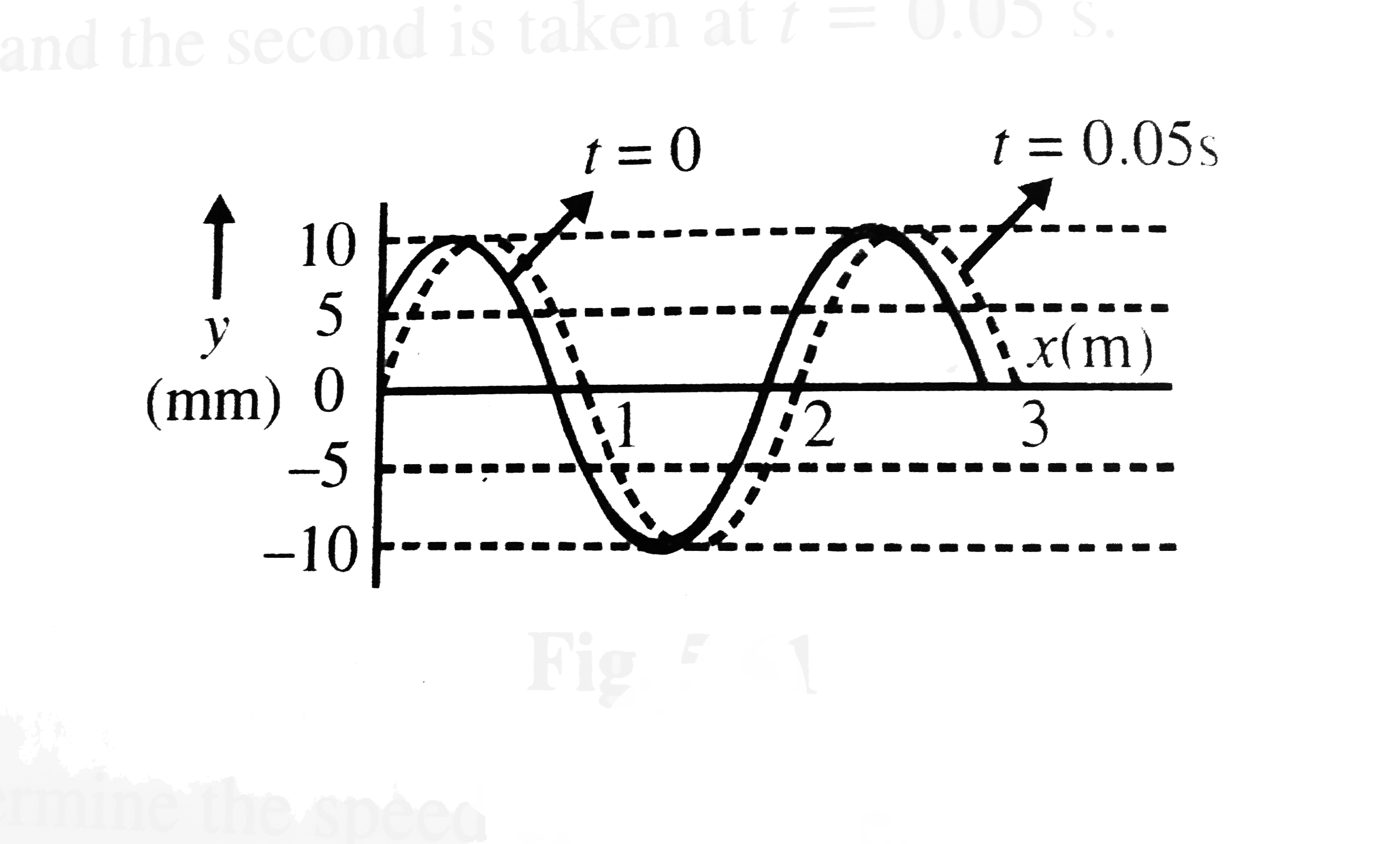
Determine the speed of the wave. Determine the frequency of the wave.View SolutionString-1 is connected with string-2. The mass per unit length in string-1 is μ1 and the mass per unit length in string-2 is 4μ1. The tension in the strings is T. A travelling wave is coming from the left. What fraction of the energy in the incident wave goes into string-2 ?
 View Solution
View SolutionA uniform string is clamped at x=0 and x = L and is vibrating in its fundamental mode. Mass per unit length of the string is μ, tension in it is T and the maximum displacement of its midpoint is A. Find the total energy stored in the string. Assume to be small so that changes in tension and length of the string can be ignored
View Solution

