The two ends of a uniform rod of thermal conductivity k are maintained at different but constant temperatures. The temperature gradientat any point on the rod is dθdl(equal to the difference in temperature per unit length). The heat flow per unit time per unit cross-section of the rod is l then which of the following statements is/are correct:
dθdl is the same for all points on the rod.
l will decrease as we move from higher to lower temperature.
l=k.dθdl
All the above options are incorrect.
The correct Answer is:A, C, D
To solve the problem, we need to analyze the heat flow through a uniform rod with constant thermal conductivity k and a temperature gradient defined by dTdL. Let's break down the steps:
Step 1: Understand the Heat Flow Equation
The heat flow Q through a rod can be described by Fourier's law of heat conduction, which states:
Q=k⋅A⋅dTdL
where:
- Q is the heat flow per unit time,
- k is the thermal conductivity of the material,
- A is the cross-sectional area of the rod,
- dTdL is the temperature gradient.
Step 2: Define the Cross-Sectional Area
In this problem, it is mentioned that the heat flow is per unit time per unit cross-section. This implies that we can consider the cross-sectional area A to be 1 (unit area). Therefore, the equation simplifies to:
Q=k⋅dTdL
Step 3: Relate Temperature Gradient to Heat Flow
From the simplified equation, we can express the temperature gradient as:
dTdL=Qk
Step 4: Analyze the Given Statements
Now, we need to evaluate the statements provided in the question. The problem states that the heat flow per unit time per unit cross-section of the rod is L. Therefore, we can write:
L=k⋅dTdL
This implies that:
dTdL=Lk
Step 5: Check the Validity of Statements
1. Statement A: If it states that L is proportional to k and dTdL, then it is correct.
2. Statement B: If it states that dTdL is constant, then it is also correct, as the rod is uniform and the temperature gradient remains the same throughout its length.
3. Statement C: If it states that L=k⋅dTdL, then it is correct based on our earlier derivation.
4. Statement D: If it states that dTdL is the same for all points on the rod, it is also correct due to the uniformity of the rod.
Conclusion
Based on the analysis, the correct statements are those that align with the derived equations and the properties of the uniform rod.
Final Answer
The correct statements are A, C, and D.
The heat flow Q through a rod can be described by Fourier's law of heat conduction, which states:
- Q is the heat flow per unit time,
- k is the thermal conductivity of the material,
- A is the cross-sectional area of the rod,
- dTdL is the temperature gradient.
In this problem, it is mentioned that the heat flow is per unit time per unit cross-section. This implies that we can consider the cross-sectional area A to be 1 (unit area). Therefore, the equation simplifies to:
From the simplified equation, we can express the temperature gradient as:
Now, we need to evaluate the statements provided in the question. The problem states that the heat flow per unit time per unit cross-section of the rod is L. Therefore, we can write:
1. Statement A: If it states that L is proportional to k and dTdL, then it is correct.
2. Statement B: If it states that dTdL is constant, then it is also correct, as the rod is uniform and the temperature gradient remains the same throughout its length.
3. Statement C: If it states that L=k⋅dTdL, then it is correct based on our earlier derivation.
4. Statement D: If it states that dTdL is the same for all points on the rod, it is also correct due to the uniformity of the rod.
Based on the analysis, the correct statements are those that align with the derived equations and the properties of the uniform rod.
The correct statements are A, C, and D.
Similar Questions
The ends of a rod of uniform thermal conductivity are maintained at different (constant) temperatures. Afer the steady state is achieved:
View SolutionOne end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of 100∘C. At the other end large quantity of ice is kept at 0∘C . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice.
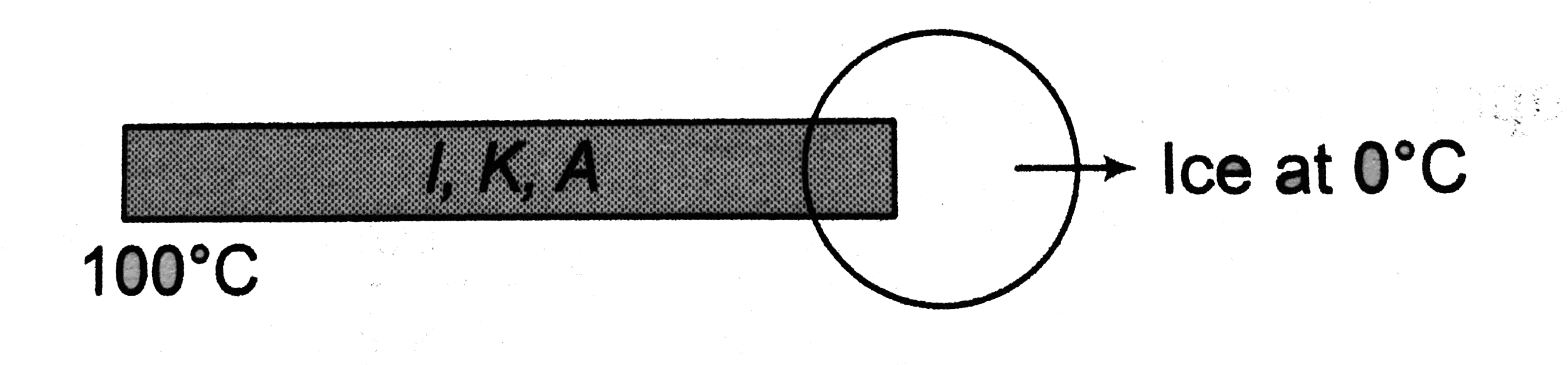 .
.
View SolutionFigure shown two adiabatic vessels, each containing a mass m of water at different temperature. The ends of a metal rod of length L, area of cross section A and thermal conductivity K, are inserted in the water as shown in the figure. Find the time taken for the difference between the temperature in the vessels to become half of the original value. The specific heat capacity of water is s. Neglect the heat capacity of the rod and the container and any loss of heat to the atmosphere.

View SolutionThe centre of mass of a non uniform rod of length L, whose mass per unit length varies as ρ=k.x2L where k is a constant and x is the distance of any point from one end is (from the same end)
View SolutionTwo identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is

View SolutionA semicircular rods is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross section of the straight rod in a given time.
View SolutionWhich of the following cylindrical rods will conduct most heat, when their ends are maintained at the same steady temperature
View SolutionA rod of length l and cross sectional area A has a variable conductivity given by K=αT, where α is a positive constant T is temperatures in Kelvin. Two ends of the rod are maintained at temperatures T1 and T2(T1>T2). Heat current flowing through the rod will be
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View Solution
