One mole of an ideal gas is warmed slowly so that it goes form the PV state (PiVi) to (3Pi,3Vi) in such a way that the pressure of the gas is directly proportional to the volume.
(a) How much work is done on the gas in the process?
(b) How is the temperature of the gas related to its volume during this process?
The correct Answer is:(a)−4PiVi(b)T=(PinRVi)V2
To solve the problem, we will break it down into two parts as stated in the question.
Part (a): Work Done on the Gas
1. Identify the Initial and Final States:
- Initial state: Pi,Vi
- Final state: 3Pi,3Vi
2. Understand the Relationship:
- The pressure P is directly proportional to the volume V. This can be expressed as:
P=kV
- From the initial state, we can find k:
Pi=kVi⟹k=PiVi
3. Equation of the Line:
- The equation of the line in the PV diagram is:
P=PiViV
4. Calculate Work Done:
- The work done on the gas during the process can be calculated as the negative of the area under the PV curve.
- The area under the curve forms a trapezium with bases Pi and 3Pi and height (3Vi−Vi)=2Vi.
- The area A of the trapezium is given by:
A=12×(Base1+Base2)×Height
A=12×(Pi+3Pi)×2Vi=12×4Pi×2Vi=4PiVi
- Therefore, the work done on the gas is:
W=−A=−4PiVi
Part (b): Relationship Between Temperature and Volume
1. Using Ideal Gas Law:
- The ideal gas law states:
PV=nRT
- For one mole of gas (n=1):
PV=RT
2. Substituting for Pressure:
- From the relationship P=PiViV:
(PiViV)V=RT
- Simplifying gives:
PiViV2=RT
3. Expressing Temperature:
- Rearranging the equation gives:
T=PiRViV2
- This shows that temperature T is proportional to the square of the volume V:
T∝V2
Final Answers:
(a) The work done on the gas is W=−4PiVi.
(b) The temperature of the gas is related to its volume by T∝V2.
- Initial state: Pi,Vi
- Final state: 3Pi,3Vi
- The pressure P is directly proportional to the volume V. This can be expressed as:
P=kV
- From the initial state, we can find k:
Pi=kVi⟹k=PiVi
- The equation of the line in the PV diagram is:
P=PiViV
- The work done on the gas during the process can be calculated as the negative of the area under the PV curve.
- The area under the curve forms a trapezium with bases Pi and 3Pi and height (3Vi−Vi)=2Vi.
- The area A of the trapezium is given by:
A=12×(Base1+Base2)×Height
A=12×(Pi+3Pi)×2Vi=12×4Pi×2Vi=4PiVi
- Therefore, the work done on the gas is:
W=−A=−4PiVi
- The ideal gas law states:
PV=nRT
- For one mole of gas (n=1):
PV=RT
- From the relationship P=PiViV:
(PiViV)V=RT
- Simplifying gives:
PiViV2=RT
- Rearranging the equation gives:
T=PiRViV2
- This shows that temperature T is proportional to the square of the volume V:
T∝V2
(a) The work done on the gas is W=−4PiVi.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 2
3 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 3
3 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
Similar Questions
In a process the pressure of a gas is inversely proportional to the square of the volume. If temperature of the gas increases, then work done by the gas:
View SolutionIn a process the pressure of a gas is inversely proportional to the square of the volume. If temperature of the gas increases, then work done by the gas:
View SolutionAn ideal gas goes from the state i to the state ∫ as shown in .the work done by the gas during the process

View SolutionIn a process, the pressure of an ideal gas is proportional to square of the volume of the gas. If the temperature of the gas increases in this process, then work done by this gas
View SolutionP-V diagram of an ideal gas is as shown in figure. Work done by the gas in the process ABCD is
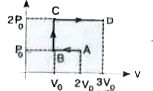
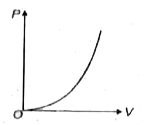
View SolutionThe variation of pressure P with volume V for an ideal diatomic gas is parabolic as shown in the figure . The molar species heat of the gas during this process is
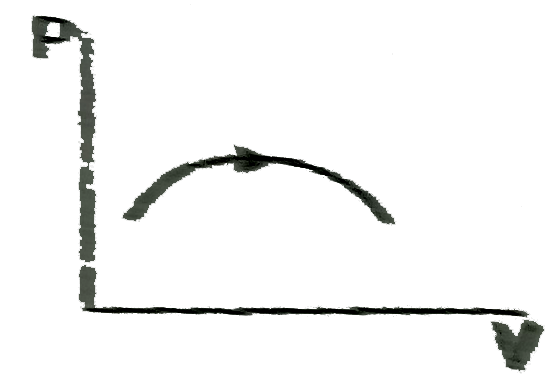
View SolutionIn figure, P−V curve of an ideal gas is given. During the process, the cumulative work done by the gas
View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio CP/CV for the gas is
View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio CP/CV for the gas is
View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio CP/CV for the gas is
View Solution
