A staright wire of length meter is carrying a current of and the magnetic field due to it is measured at a point distant from it. If the wire is to be bent into a circles and is to carry the same current as before, the ratio of the magnetic field at its centre to that obtained in the first case would be
The correct Answer is:D
To solve the problem, we need to calculate the magnetic field produced by a straight wire and then compare it to the magnetic field produced by a circular wire of the same length carrying the same current.
1. Calculate the Magnetic Field due to the Straight Wire (B1):
The formula for the magnetic field (B) at a distance (r) from a long straight wire carrying current (I) is given by:
B=μ04π⋅2Ir
Here, μ0=4π×10−7T m/A, I=2A, and r=0.01m (1 cm).
Substituting the values:
B1=4π×10−74π⋅2×20.01
Simplifying:
B1=10−7⋅40.01=10−7⋅400=4×10−5T
2. Determine the Length of the Wire and Radius of the Circle:
The length of the wire is given as π2 meters. When bent into a circle, the circumference (C) of the circle is equal to the length of the wire:
C=2πr=π2
Solving for the radius (r):
r=π22π=π2m
3. Calculate the Magnetic Field at the Center of the Circular Wire (B2):
The formula for the magnetic field at the center of a circular loop carrying current (I) is:
B=μ0I2r
Substituting the values:
B2=4π×10−7⋅22⋅π2=4π×10−7⋅2π=8×10−7T
4. Calculate the Ratio of the Magnetic Fields (B2/B1):
Now we find the ratio of the magnetic field at the center of the circular wire to the magnetic field due to the straight wire:
Ratio=B2B1=8×10−74×10−5=8400=150
Thus, the ratio of the magnetic field at the center of the circular wire to that obtained in the first case is:
Ratio=1:50
The formula for the magnetic field (B) at a distance (r) from a long straight wire carrying current (I) is given by:
B=μ04π⋅2Ir
Here, μ0=4π×10−7T m/A, I=2A, and r=0.01m (1 cm).
B1=4π×10−74π⋅2×20.01
Simplifying:
B1=10−7⋅40.01=10−7⋅400=4×10−5T
The length of the wire is given as π2 meters. When bent into a circle, the circumference (C) of the circle is equal to the length of the wire:
C=2πr=π2
Solving for the radius (r):
r=π22π=π2m
The formula for the magnetic field at the center of a circular loop carrying current (I) is:
B=μ0I2r
Substituting the values:
B2=4π×10−7⋅22⋅π2=4π×10−7⋅2π=8×10−7T
Now we find the ratio of the magnetic field at the center of the circular wire to the magnetic field due to the straight wire:
Ratio=B2B1=8×10−74×10−5=8400=150
Ratio=1:50
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Subjective type
10 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
Knowledge Check
If a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
A5.34×10−5TB8.34×10−5TC9.6×10−5TD10.2×10−5T
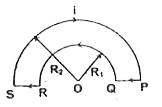
The wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,
View SolutionA transmission wire carries a current of 100A. What would be the magnetic field B at a point on the road if the wire is 8 m above the road?
View SolutionA wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
View SolutionA wire of length 2 m carrying a current of 1 A is bend to form a circle. The magnetic moment of the coil is (in Am2)
View SolutionA wire of length l meter carrying current i ampere is bent in form of circle. Magnetic moment is
View SolutionA long wire bent as shown in fig. carries current I. If the radius of the semicircular portion is a, the magnetic field at centre C is

View SolutionA wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
View Solution
