A cylinderical glass rod of radius 0.1m and refractive index √3 lies on a horizontal plane mirror. A horizontal ray of light moving perpendicular to the axis of the rod is incident on it. At what height from the mirror should the ray be incident so that it leaves the rod at a height of 0.1m above the plane mirror? At what centre to centre distance a second similar rod, parallel to the first, be placed on the mirror, such that the emergent ray from the second rod is in line with the incident ray on the first rod?

The correct Answer is:A, C
(i) PO=OQ
∴∠OPQ=∠OQP=r(say)
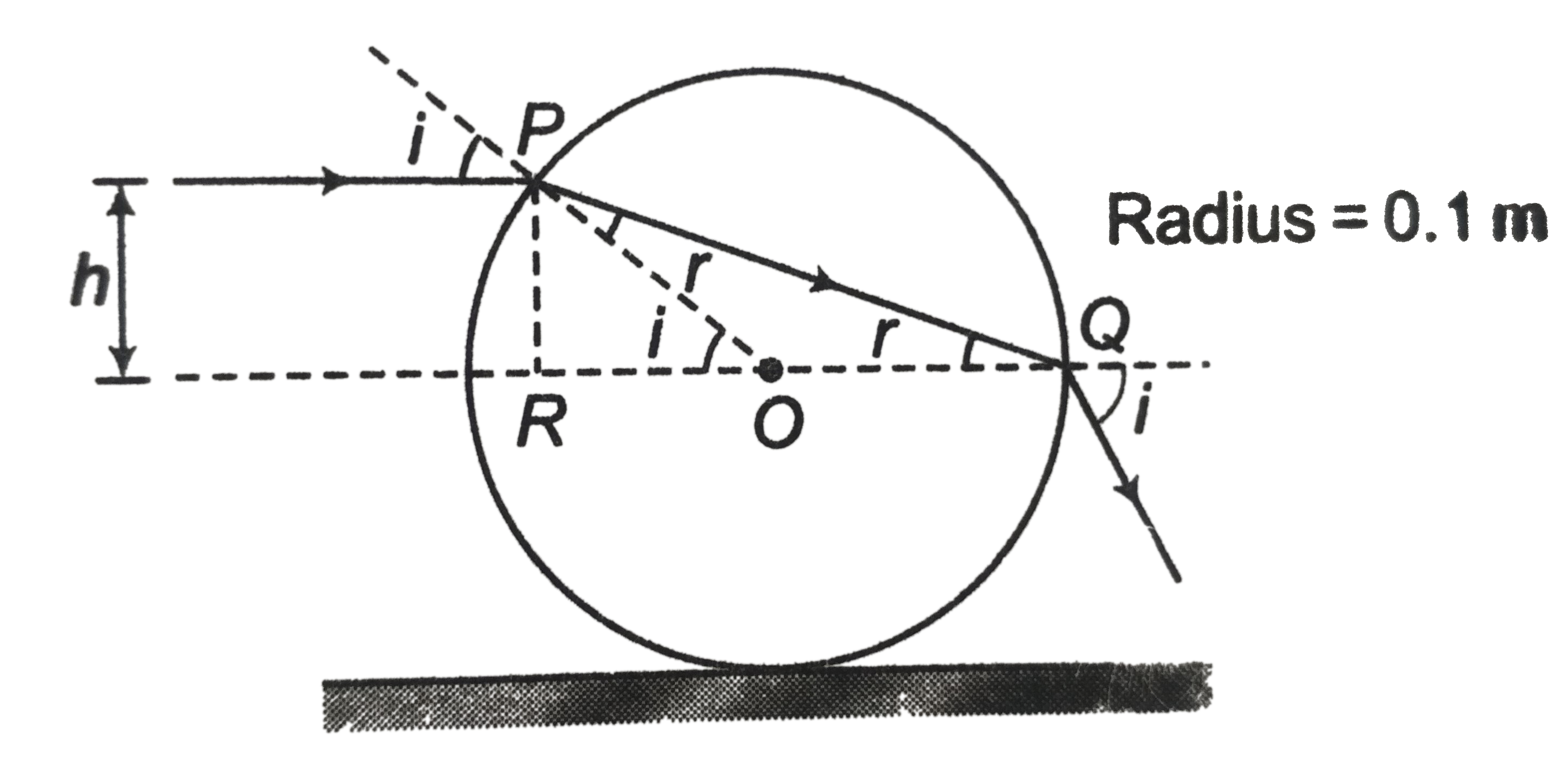
Also, i=r+r=2r
In ΔPQR,h=OPsinI=0.1sint
=0.1sin2r
or h=.0.2simrcosr……(i)
Also √3=sinisinr=2sinrcosrsinr
=2cosr
∴r=30∘
Substituting in Eq. (i), we get
h=0.2×12×√32
=0.086m.
Hence, height from the mirror is
0.1+0.086=0.186m
(ii) Use the principle of reversiblity
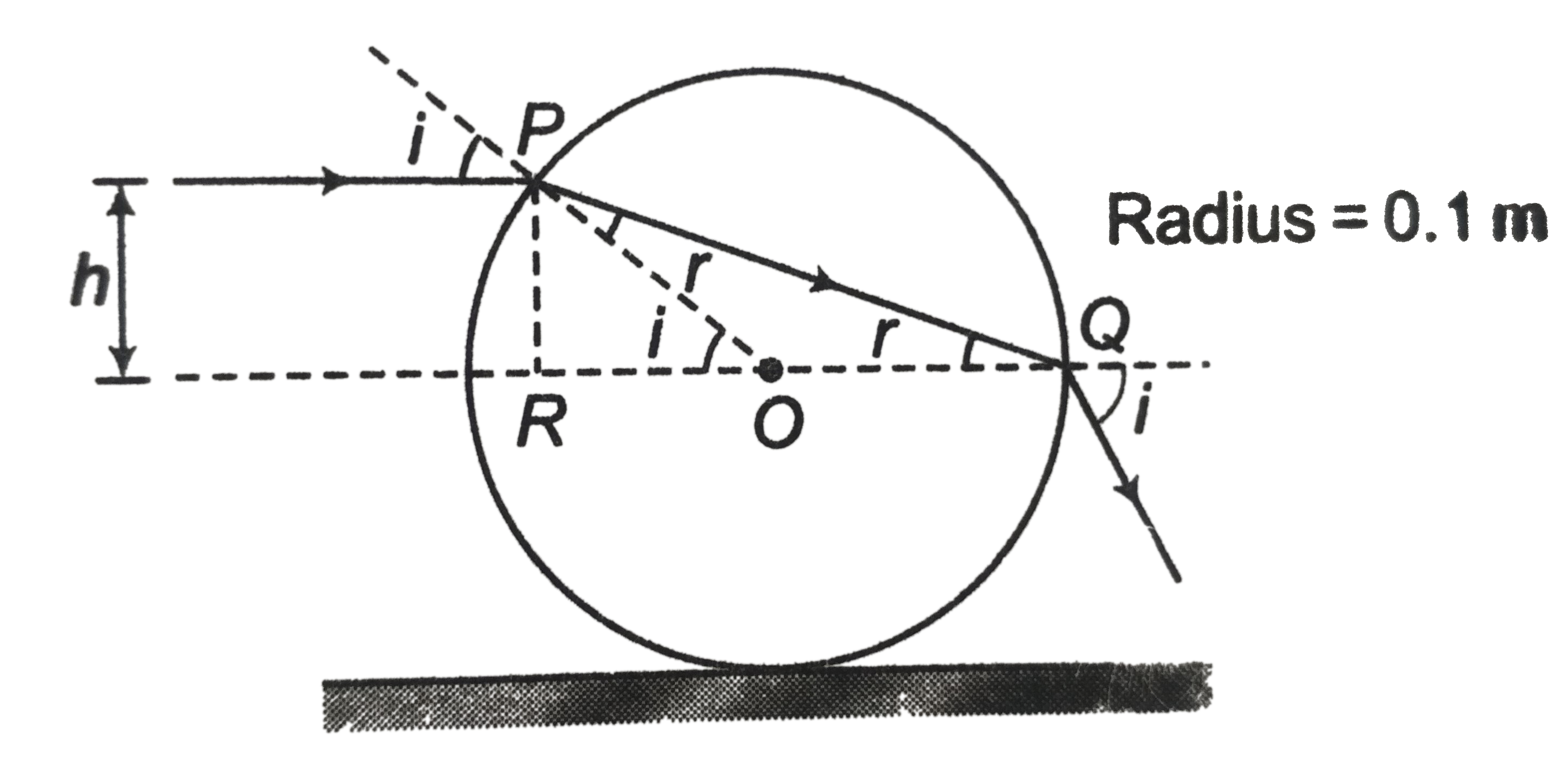
i=2r=60∘
Now, QSMS=coti=cot60∘=1√3
∴QS=MS√3=0.1√3
∴ The disered distance,
OC=2×0.1+2×0.1√3
0.315
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Single Correct
41 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Single Correct Option
3 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Subjective
29 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions

A plane wave front of light is incident on a plane mirror. Intensity is maximum at P when
View SolutionRays of light are incident on a plane mirror at 40∘. At what angle with the first should a second mirror be placed such that the rays emerge from the second mirror parallel to the first mirror.
View SolutionTwo plane mirrors are inclined to each other at an angle 60∘ if a ray of light incident on first mirror parallel to the second mirror, it is reflected from the second mirror
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionFind the angle between two plane mirrors such that a ray of light incident on the first mirror and parallel to the second mirror is reflected from the second mirror, parallel to the first mirror.
View SolutionA ray of light falls normally on a plane mirror. What is the angle of incidence ?
View SolutionDraw the incident ray and the reflected ray. if a light ray is incident on a plane mirror with the angle of incidence 30∘.
View SolutionA prism having an apex angle of 4∘ and refractive index of 1.50 is located in front of a vertical plane mirror as shown in the figure. A horizontal ray of light is incident on the prism. The total angle through which the ray is deviated is:
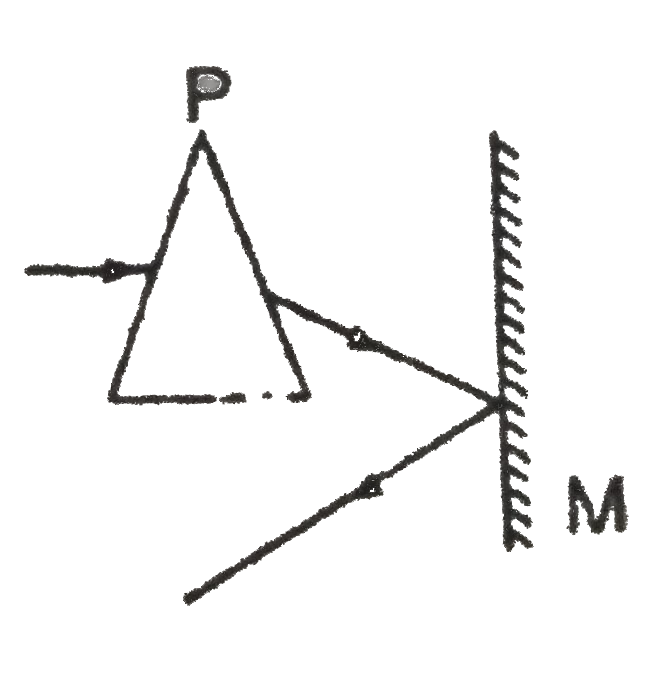
View SolutionA ray of light is incident on a plane mirror at an angle of incidence of 30∘. The deviation produced by the mirror is
View SolutionTwo plane mirrors are inclined to each other such that a ray of light incident on the first mirror and parallel to the second is reflected from the second mirror parallel to the first mirror. Determine the angle between the two mirrors:
View Solution
