If wavelength is equal to the distance travelled by the electron in one second then
The correct Answer is:D
To solve the problem, we start with the given information that the wavelength (λ) is equal to the distance traveled by the electron in one second.
1. Understanding the Relationship:
We know from de Broglie's hypothesis that the wavelength (λ) of a moving particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle.
2. Momentum Definition:
The momentum p of a particle can be expressed as:
p=mv
where m is the mass of the particle and v is its velocity.
3. Substituting Momentum into Wavelength Formula:
Substituting the expression for momentum into the wavelength formula gives:
λ=hmv
4. Distance Traveled by Electron:
According to the problem, the distance traveled by the electron in one second is equal to the wavelength. Therefore, we can express this as:
Distance=v=λ
5. Setting Up the Equation:
Since we have established that v=λ, we can substitute this into our wavelength equation:
λ=hmλ
6. Rearranging the Equation:
To eliminate λ from the denominator, we multiply both sides by λ:
λ2=hm
7. Solving for Wavelength:
Taking the square root of both sides gives us:
λ=√hm
Final Result:
Thus, the wavelength of the electron, given that it is equal to the distance traveled in one second, is:
λ=√hm
We know from de Broglie's hypothesis that the wavelength (λ) of a moving particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle.
The momentum p of a particle can be expressed as:
p=mv
where m is the mass of the particle and v is its velocity.
Substituting the expression for momentum into the wavelength formula gives:
λ=hmv
According to the problem, the distance traveled by the electron in one second is equal to the wavelength. Therefore, we can express this as:
Distance=v=λ
Since we have established that v=λ, we can substitute this into our wavelength equation:
λ=hmλ
To eliminate λ from the denominator, we multiply both sides by λ:
λ2=hm
Taking the square root of both sides gives us:
λ=√hm
Thus, the wavelength of the electron, given that it is equal to the distance traveled in one second, is:
λ=√hm
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercises Assertion And Reason
21 Videos
- ATOMIC STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercises Integer
11 Videos
- ATOMIC STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercises Multiple Correct
45 Videos
- APPENDIX - INORGANIC VOLUME 1BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - APPENDIX - INORGANIC VOLUME 1EXERCISE - chapter-7 Single correct answer
1 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Archives Subjective
15 Videos
Similar Questions
Knowledge Check
In the given v-t graph the distance travelled by the body in 5 seconds will be
 A100 mB80 mC40 mD20 m
A100 mB80 mC40 mD20 mA rod 6 inches long is pivoted at a one end. If the free end of the 165 revolutions per minute, what is the total distance, in inches, traveled by the end of the rod in one seconds?
A14.5πB16.5πC29πD33π
What is the ratio between the distance travelled by the oscillator in one time period and amplitude?
View SolutionThe speed of a car as a function of time is shown in figure.
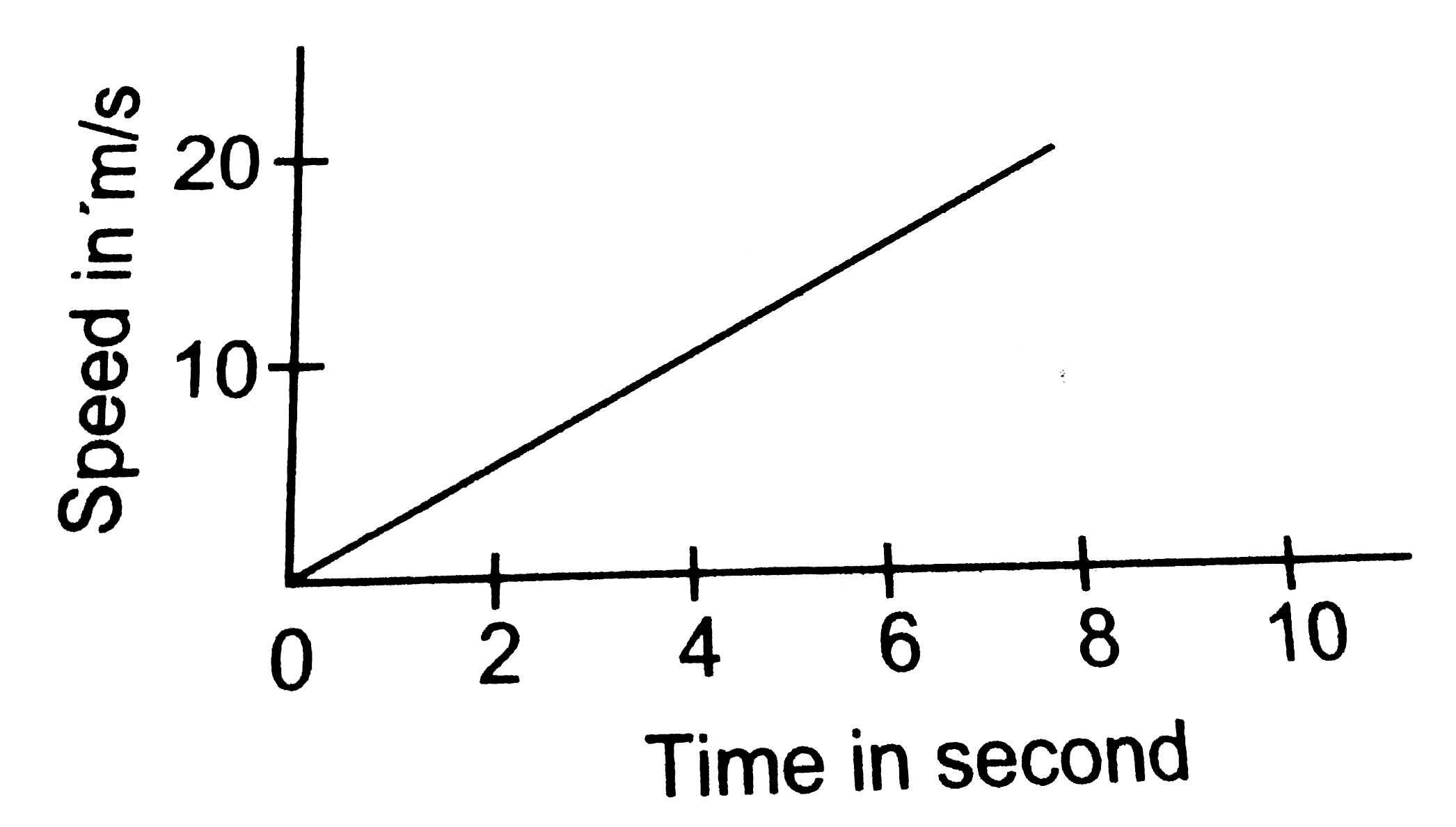
Find the distance travelled by the car in 8 seconds and its acceleration.
View SolutionThe speed of a car increases uniformly from zero to 10ms−1 in 2s and then remains constant (figure)

a. Find the distance travelled by the car in the first two seconds.
b. Find the distance travelled by the car in the next two seconds.
c. Find the total distance travelled in 4s.
View SolutionA particle is thrown with any velocity vertically upward, the distance travelled by the particle in first second of its decent is
View SolutionThe motion of a particle is described by the equation at u=at.The distance travelled by the particle in the first 4 seconds
View SolutionFind the approximate total distance traveled by an electron in the time interval in which its displacement in one meter along the wire.
View Solution
