A particle is thrown with any velocity vertically upward, the distance travelled by the particle in first second of its decent is
g
g2
g4
Cannot be calculated
The correct Answer is:B
To solve the problem of finding the distance traveled by a particle in the first second of its descent after being thrown vertically upward, we can follow these steps:
1. Understand the Motion:
- A particle is thrown vertically upward with an initial velocity v.
- It rises until it reaches the highest point, where its velocity becomes 0.
- After reaching the highest point, the particle begins its descent.
2. Identify the Initial Conditions for Descent:
- At the highest point, the initial velocity u for the descent is 0 m/s (since it momentarily stops before falling down).
- The acceleration g (due to gravity) acts downward and has a value of approximately 9.81m/s2.
3. Use the Kinematic Equation:
- We use the equation of motion for the distance traveled under uniform acceleration:
s=ut+12gt2
- Here, s is the distance traveled, u is the initial velocity, g is the acceleration due to gravity, and t is the time.
4. Substitute the Known Values:
- Since u=0 (initial velocity at the highest point) and t=1 second (the time of descent we are interested in), we can substitute these values into the equation:
s=0⋅1+12⋅g⋅(1)2
- This simplifies to:
s=12g
5. Calculate the Distance:
- Substituting g≈9.81m/s2:
s=12⋅9.81≈4.905m
6. Conclusion:
- The distance traveled by the particle in the first second of its descent is approximately 4.905m.
Final Answer:
The distance traveled by the particle in the first second of its descent is approximately 4.905m.
- A particle is thrown vertically upward with an initial velocity v.
- It rises until it reaches the highest point, where its velocity becomes 0.
- After reaching the highest point, the particle begins its descent.
- At the highest point, the initial velocity u for the descent is 0 m/s (since it momentarily stops before falling down).
- The acceleration g (due to gravity) acts downward and has a value of approximately 9.81m/s2.
- We use the equation of motion for the distance traveled under uniform acceleration:
s=ut+12gt2
- Here, s is the distance traveled, u is the initial velocity, g is the acceleration due to gravity, and t is the time.
- Since u=0 (initial velocity at the highest point) and t=1 second (the time of descent we are interested in), we can substitute these values into the equation:
s=0⋅1+12⋅g⋅(1)2
- This simplifies to:
s=12g
- Substituting g≈9.81m/s2:
s=12⋅9.81≈4.905m
- The distance traveled by the particle in the first second of its descent is approximately 4.905m.
The distance traveled by the particle in the first second of its descent is approximately 4.905m.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - B)
33 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - C)
36 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISE
29 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
Similar Questions
A body is projected with a velocity 60ms−1 vertically upwards the distance travelled in last second of its motion is [g=10ms−1]
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
View SolutionThe position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
View SolutionA particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
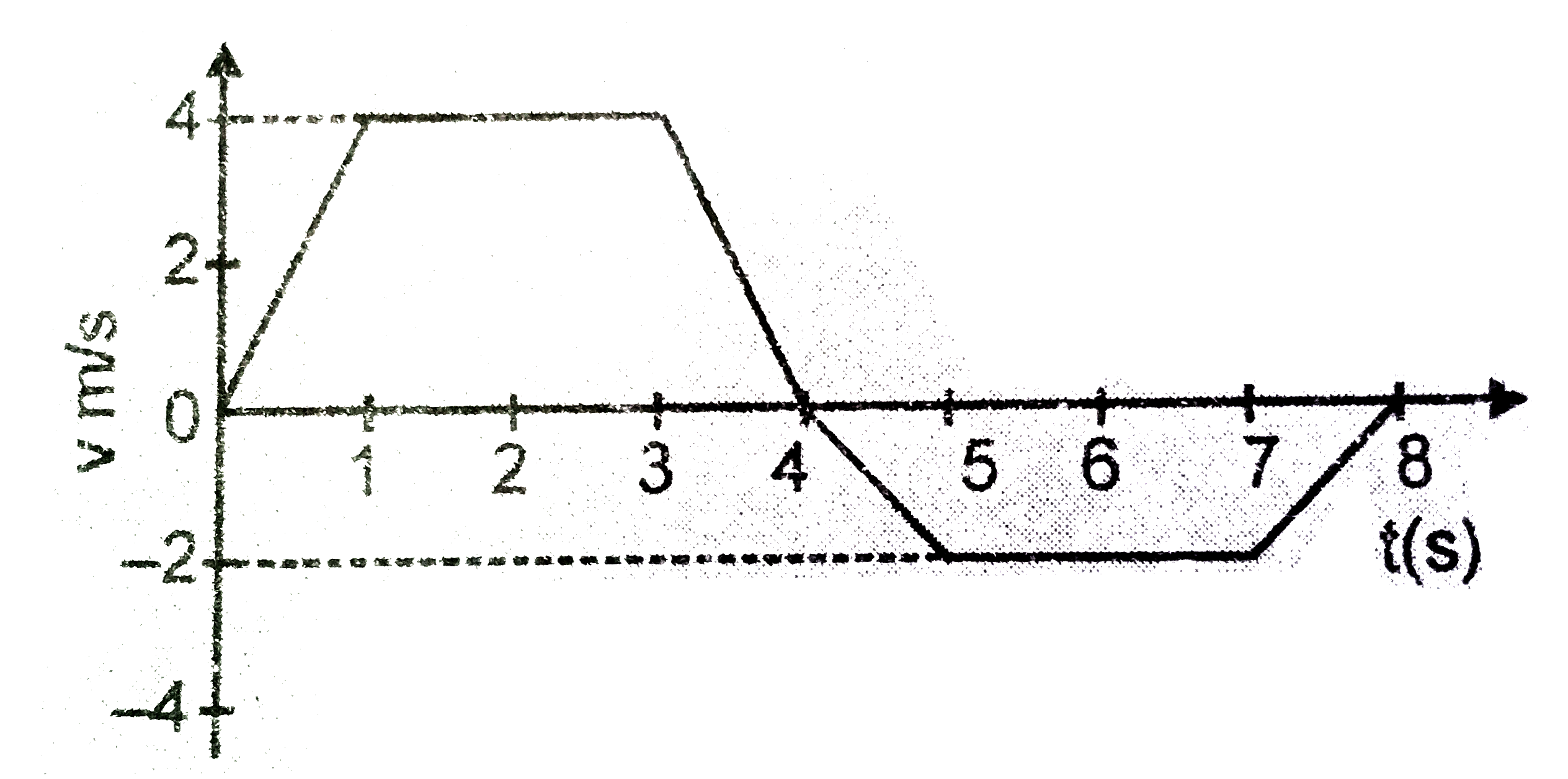
View SolutionIf a ball is thrown vertically upwards with speed u, the distance covered during the last t second of its ascent is
View SolutionThe motion of a particle is described by the equation at u=at.The distance travelled by the particle in the first 4 seconds
View SolutionA particle starting from rest moves in a straight line with acceleration as shown in the a-t graph. Find the distance (in m) travelled by the particle in the first four seconds from start of its motion.
Q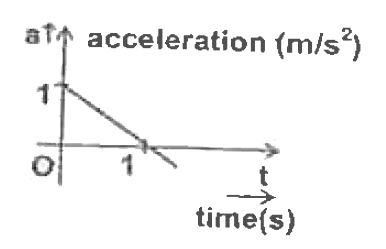
View SolutionA particle is dropped from the top of a high building 360 m. The distance travelled by the particle in ninth second is (g=10m/s2)
View SolutionThe variation of velocity of a particle with time moving along a straight line is illustrated in the following figure. The distance travelled by the particle in four seconds is.
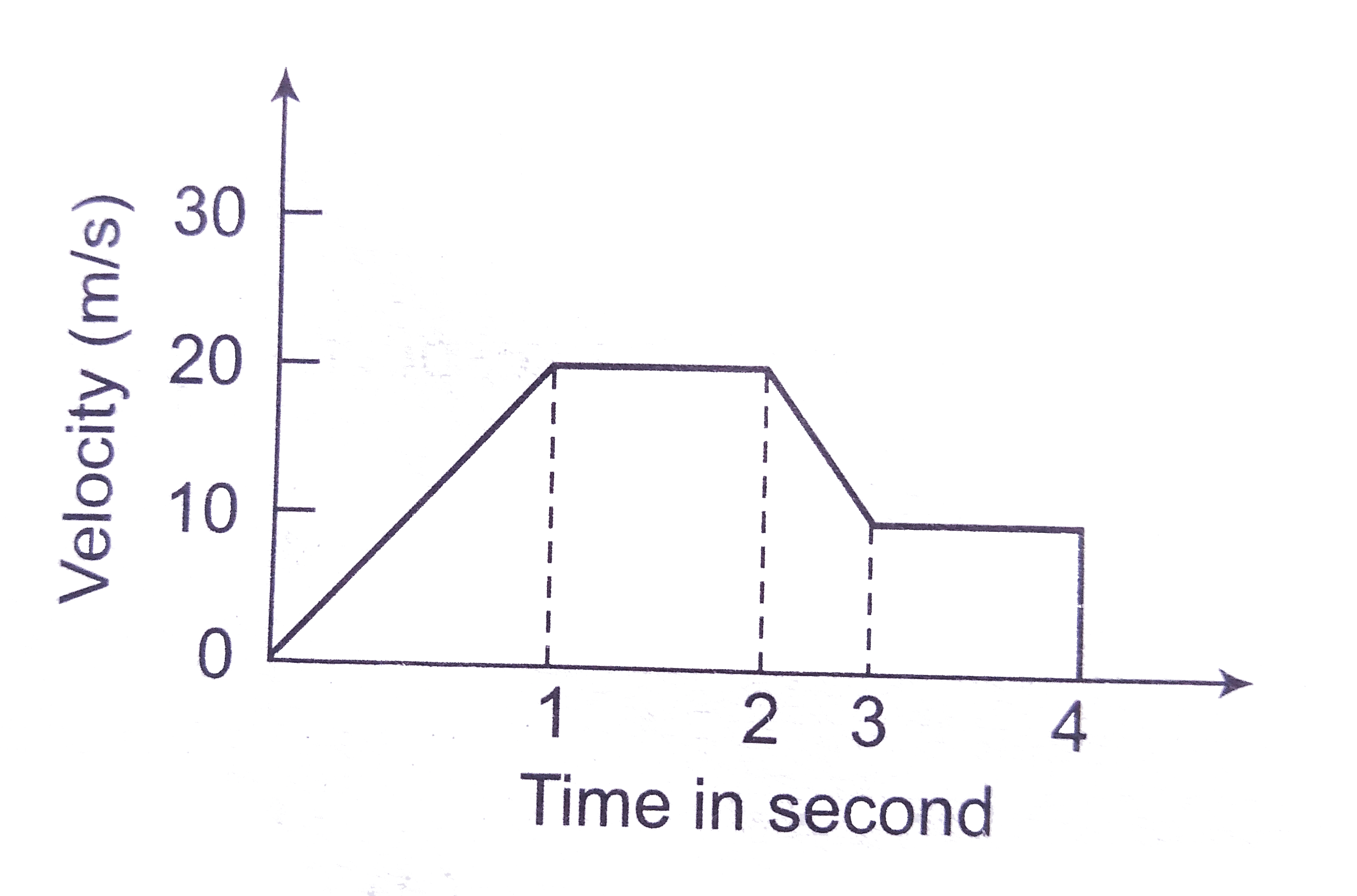
View SolutionThe distance travelled by a body during last second of its upward journey is d when the body is projected with certain velocity vertically up. If the velocity of projection is doubled, the distance travelled by the body during last second of its upward journey is
View Solution
