For and elementary reaction
2Ak1⇐⇒k2B, the rate of disappearance of A iss equal to
(a) 2k1k2[A]2
(b) −2k1[A]2+2k2[B]
( c) 2k1[A]2−2k2[B]
(d) (2k1−k2)[A]
To solve the problem regarding the rate of disappearance of A in the reaction 2A⇌B, we will follow these steps:
Step 1: Write the Rate Expressions
For the forward reaction 2A→B, the rate can be expressed as:
\( R_f = k_1 (A)^2 \)
where \( k_1 \) is the rate constant for the forward reaction.
For the reverse reaction B→2A, the rate can be expressed as:
\( R_b = k_2 (B) \)
where \( k_2 \) is the rate constant for the reverse reaction.
Step 2: Determine the Overall Rate of Disappearance of A
The overall rate of disappearance of A is given by the difference between the rate of the forward reaction and the rate of the reverse reaction:
\( \text{Rate of disappearance of A} = R_f - R_b \)
Substituting the expressions for \( R_f \) and \( R_b \):
\( \text{Rate of disappearance of A} = k_1 (A)^2 - k_2 (B) \)
Step 3: Adjust for Stoichiometry
Since the reaction involves 2 moles of A, we need to account for the stoichiometry in the rate expression. Therefore, we multiply the rate of disappearance of A by 2:
\( \text{Rate of disappearance of A} = 2(k_1 (A)^2 - k_2 (B)) \)
Step 4: Final Expression
This simplifies to:
\( \text{Rate of disappearance of A} = 2k_1 (A)^2 - 2k_2 (B) \)
Conclusion
Thus, the correct expression for the rate of disappearance of A is:
\( \text{Rate of disappearance of A} = 2k_1 (A)^2 - 2k_2 (B) \)
From the options provided, this corresponds to option (c):
\( 2k_1 (A)^2 - 2k_2 (B) \)
---
For the forward reaction 2A→B, the rate can be expressed as:
\( R_f = k_1 (A)^2 \)
where \( k_1 \) is the rate constant for the forward reaction.
\( R_b = k_2 (B) \)
where \( k_2 \) is the rate constant for the reverse reaction.
The overall rate of disappearance of A is given by the difference between the rate of the forward reaction and the rate of the reverse reaction:
\( \text{Rate of disappearance of A} = R_f - R_b \)
\( \text{Rate of disappearance of A} = k_1 (A)^2 - k_2 (B) \)
Since the reaction involves 2 moles of A, we need to account for the stoichiometry in the rate expression. Therefore, we multiply the rate of disappearance of A by 2:
\( \text{Rate of disappearance of A} = 2(k_1 (A)^2 - k_2 (B)) \)
This simplifies to:
\( \text{Rate of disappearance of A} = 2k_1 (A)^2 - 2k_2 (B) \)
Thus, the correct expression for the rate of disappearance of A is:
\( \text{Rate of disappearance of A} = 2k_1 (A)^2 - 2k_2 (B) \)
\( 2k_1 (A)^2 - 2k_2 (B) \)
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Solved Example
52 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Ex 4.1 (Objective)
9 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
Knowledge Check
If (k+1k)2=16, then k2+1k2=
A4B8C12D14
For an elementary chemical reaction, A2k1⇐===⇒k−12A, the expression for d[A]dt is
View SolutionFor the following elementary first order reaction:
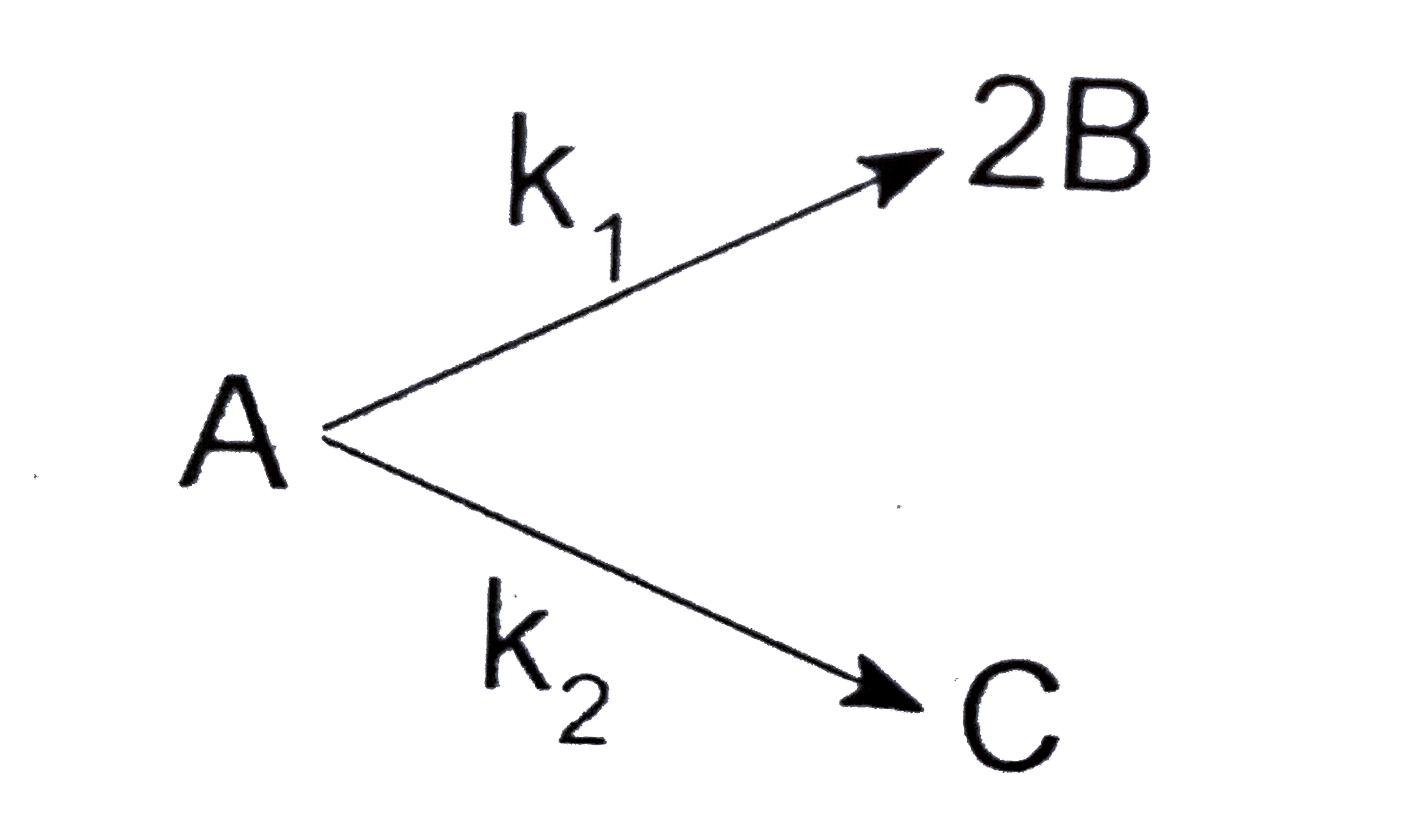
If k2=2k1, then % of B in overall product is:
View SolutionMechanism of the reaction is:
Ak1−−→B,2Ak2−−→C+D
What is −d[A]dt ?
View SolutionConisder the following reactions:
I. A+Bk1⇐⇒k−1C
II. C+Bk2−−→D
Then k1[A][B]−k−1[C]−k2[C][B] is equal to
(a) −d[A]dt
(b)−d[B]dt
(c)d[C]dt
(d)d[D]dt
View SolutionMechanism of the reaction is:
Ak2⇐⇒k1B ...(i)
B+Ak3⇐⇒C ...(ii)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯2A→C––––––––– ...(iii)
What is (a) −d[A]dt, (b ) d[C]dt
View SolutionFor a reversible reaction AK1⇐===⇒K2B rate constant K1 (forward) = 1015e−200T and K2 (backward) = 1012e−200T. What is the value of −ΔG∘2.303RT ?
View SolutionMechanism of the reaction is:
A2k⇐⇒k'2A
A+B2k2−−→C+B
B+A2k2−−→C+A
What is−d[A2]dt
View Solution
