A satellite of mass m orbits the earth in an elliptical orbit having aphelion distance ra and perihelion distance rp. The period of the orbit is T. The semi-major and semi-minor axes of the ellipse are ra+rp2 and √rpra respectively. The angular momentum of the satellite is: (A) 2mπ(rB+rp)√rarpT (B) mπ(ra+rp)√rarp2T (C) mπ(ra+rp)√rarp4T (D) mπ(ra+rp)√rarpT
2mπ(rB+rp)√rarpT
mπ(ra+rp)√rarp2T
mπ(ra+rp)√rarp4T
mπ(ra+rp)√rarpT
The correct Answer is:C
To find the angular momentum of a satellite orbiting the Earth in an elliptical orbit, we can follow these steps:
Step 1: Understand the parameters of the elliptical orbit
The satellite has:
- Aphelion distance ra
- Perihelion distance rp
- Period of the orbit T
- Semi-major axis a=ra+rp2
- Semi-minor axis b=√rarp
Step 2: Use Kepler's Second Law
Kepler's Second Law states that the area swept out by the satellite in a given time is constant. The relationship can be expressed as:
dAdt=L2m
where L is the angular momentum and m is the mass of the satellite.
Step 3: Calculate the area of the ellipse
The total area A of the elliptical orbit is given by:
A=πab
Substituting the values of a and b:
A=π(ra+rp2)(√rarp)
Step 4: Relate area to angular momentum
The total area covered in time T is:
A=L2m⋅T
Setting the two expressions for area equal gives:
L2m⋅T=π(ra+rp2)(√rarp)
Step 5: Solve for angular momentum L
Rearranging the equation to solve for L:
L=2mπ(ra+rp2)(√rarp)T
This simplifies to:
L=mπ(ra+rp)√rarpT
Conclusion
Thus, the angular momentum of the satellite is:
L=mπ(ra+rp)√rarpT
This corresponds to option (D).
The satellite has:
- Aphelion distance ra
- Perihelion distance rp
- Period of the orbit T
- Semi-major axis a=ra+rp2
- Semi-minor axis b=√rarp
Kepler's Second Law states that the area swept out by the satellite in a given time is constant. The relationship can be expressed as:
dAdt=L2m
where L is the angular momentum and m is the mass of the satellite.
The total area A of the elliptical orbit is given by:
A=πab
Substituting the values of a and b:
A=π(ra+rp2)(√rarp)
The total area covered in time T is:
A=L2m⋅T
Setting the two expressions for area equal gives:
L2m⋅T=π(ra+rp2)(√rarp)
Rearranging the equation to solve for L:
L=2mπ(ra+rp2)(√rarp)T
This simplifies to:
L=mπ(ra+rp)√rarpT
Thus, the angular momentum of the satellite is:
L=mπ(ra+rp)√rarpT
This corresponds to option (D).
Topper's Solved these Questions
- TEST PAPERBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPEREXERCISE - CHEMISTRY
24 Videos
- TEST PAPERBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPEREXERCISE - MATHEMATICS
48 Videos
- SEQUENCE & SERIES BOOK - RESONANCE ENGLISHCHAPTER - SEQUENCE & SERIES EXERCISE - EXERCISE -2 (PART-II : PREVIOUSLY ASKED QUESTION OF RMO)
3 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
259 Videos
Similar Questions
A satellite of mass m orbits the earth in an elliptical orbit having aphelion distance ra ad perihelion distance rp. The period of the orbit is T. The semi-major and semi-minor axes of the ellipse are a and b respectively. The angular momentum of the satellite is
View SolutionA planet of mass m revolves in elliptical orbit around the sun of mass M so that its maximum and minimum distance from the sun equal to ra and rp respectively. Find the angular momentum of this planet relative to the sun.
View SolutionA satellite is launched into a circular orbit of radius R around the earth while a second satellite is launched into an orbit of radius 1.02R. The percentage difference in the time period is:
View SolutionIf a satellite is revolving around a plenet of mass M in an elliptical orbit of semi-major axis a. Show that the orbital speed of the satellite when it is a distance r from the focus will be given by
υ2=GM[2r−1a]
View SolutionTwo satellites A and B of masses m1 and m2(m1=2m2) are moving in circular orbits of radii r1 and r2(r1=4r2), respectively, around the earth. If their periods are TA and TB, then the ratio TA/TB is
View SolutionA system of binary stars of mass mA and mB are moving in circular orbits of radii rA and rB respectively. If TA and TB are at the time periods of masses mA and mB respectively then
View SolutionLet the speed of the planet at the perihelion P in figure be vP and the Sun planet distance SP be rP. Relater rP,vP to the corresponding quantities at the aphelion (rA,vA). Will the planet take equal times to transverse BAC and CPB?

View SolutionThe variation of radial probability density R2 (r) as a function of distance r of the electron from the nucleus for 3p orbital:
(A)(a)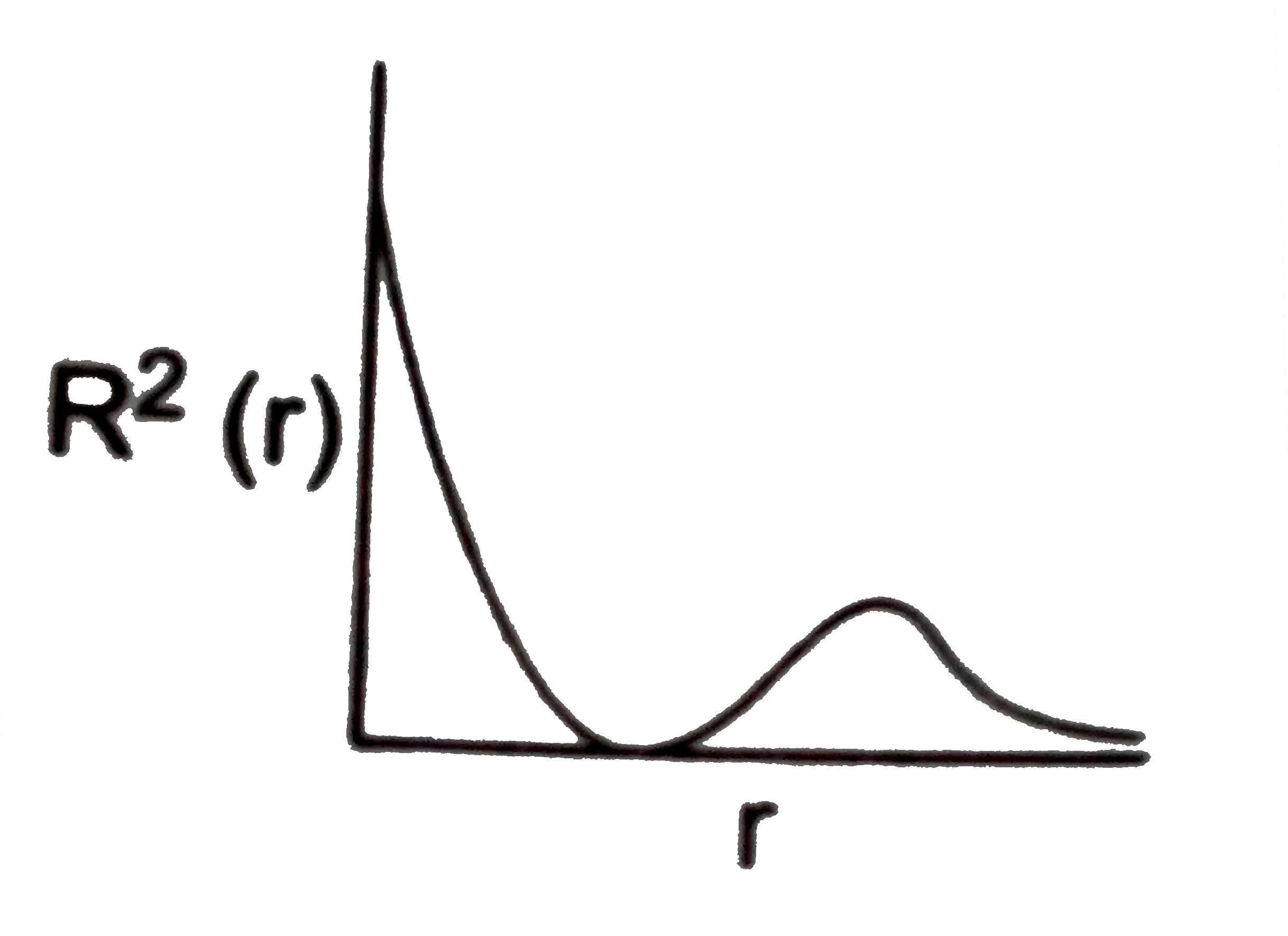
(b) (b)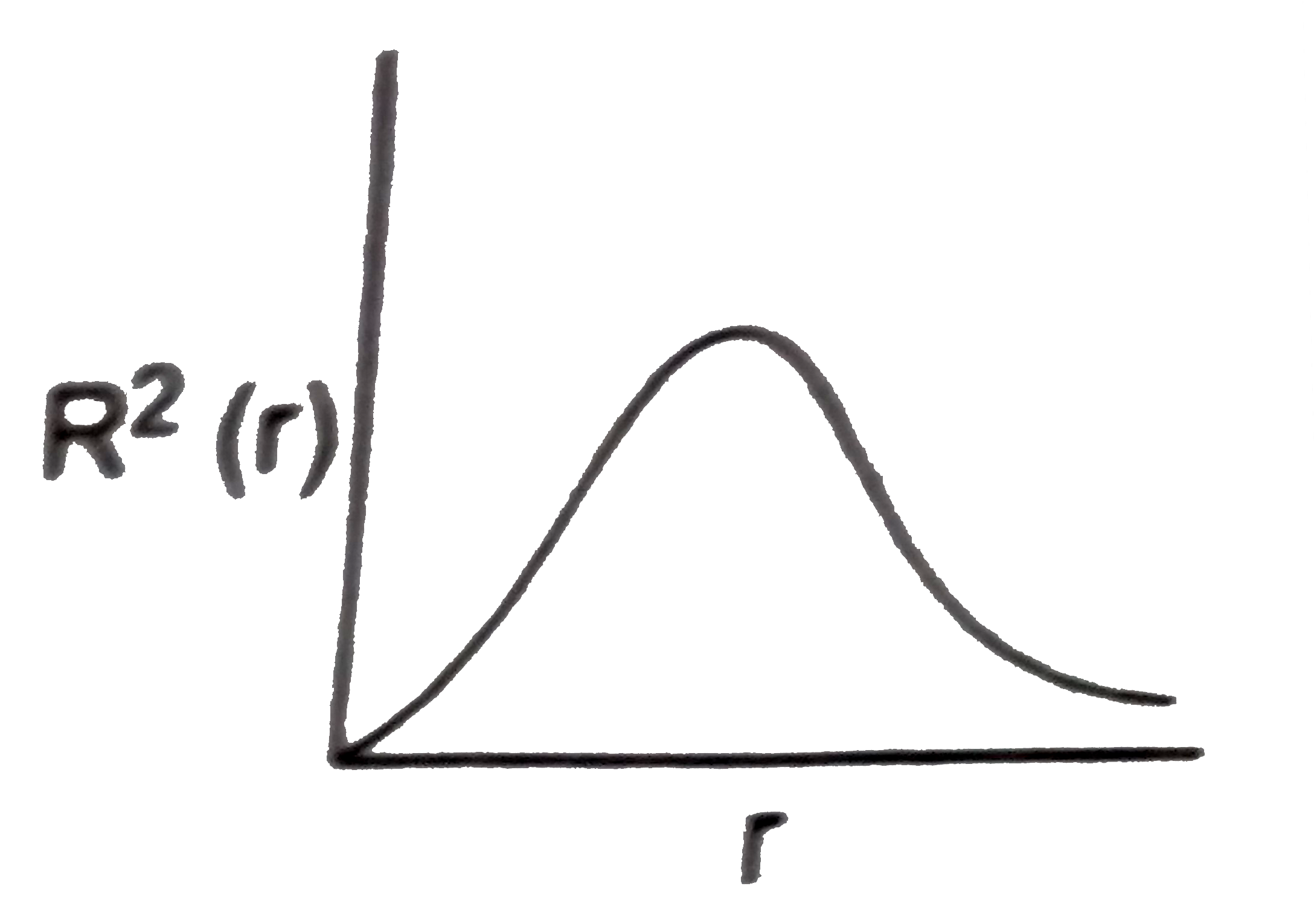
(c)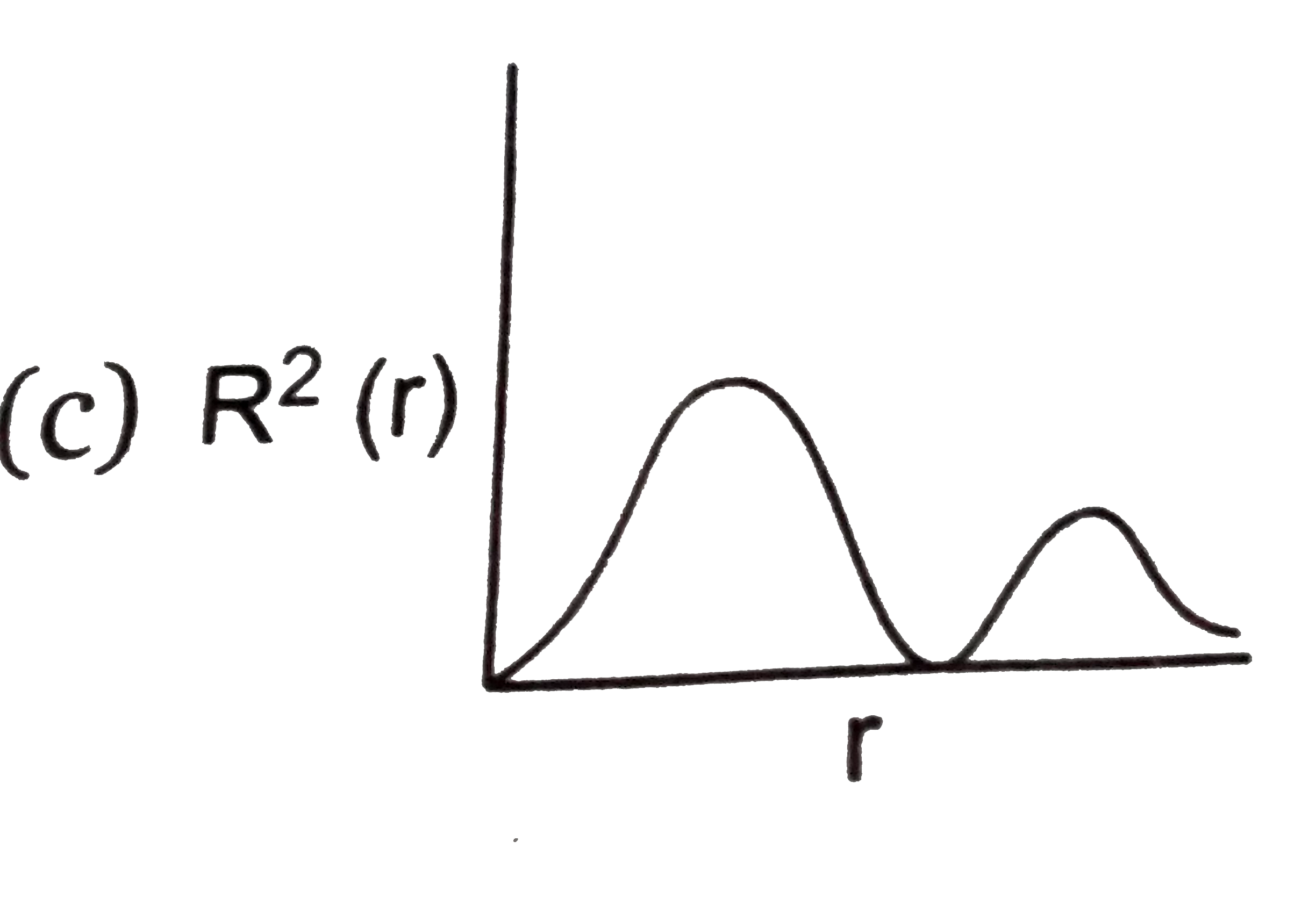
(d)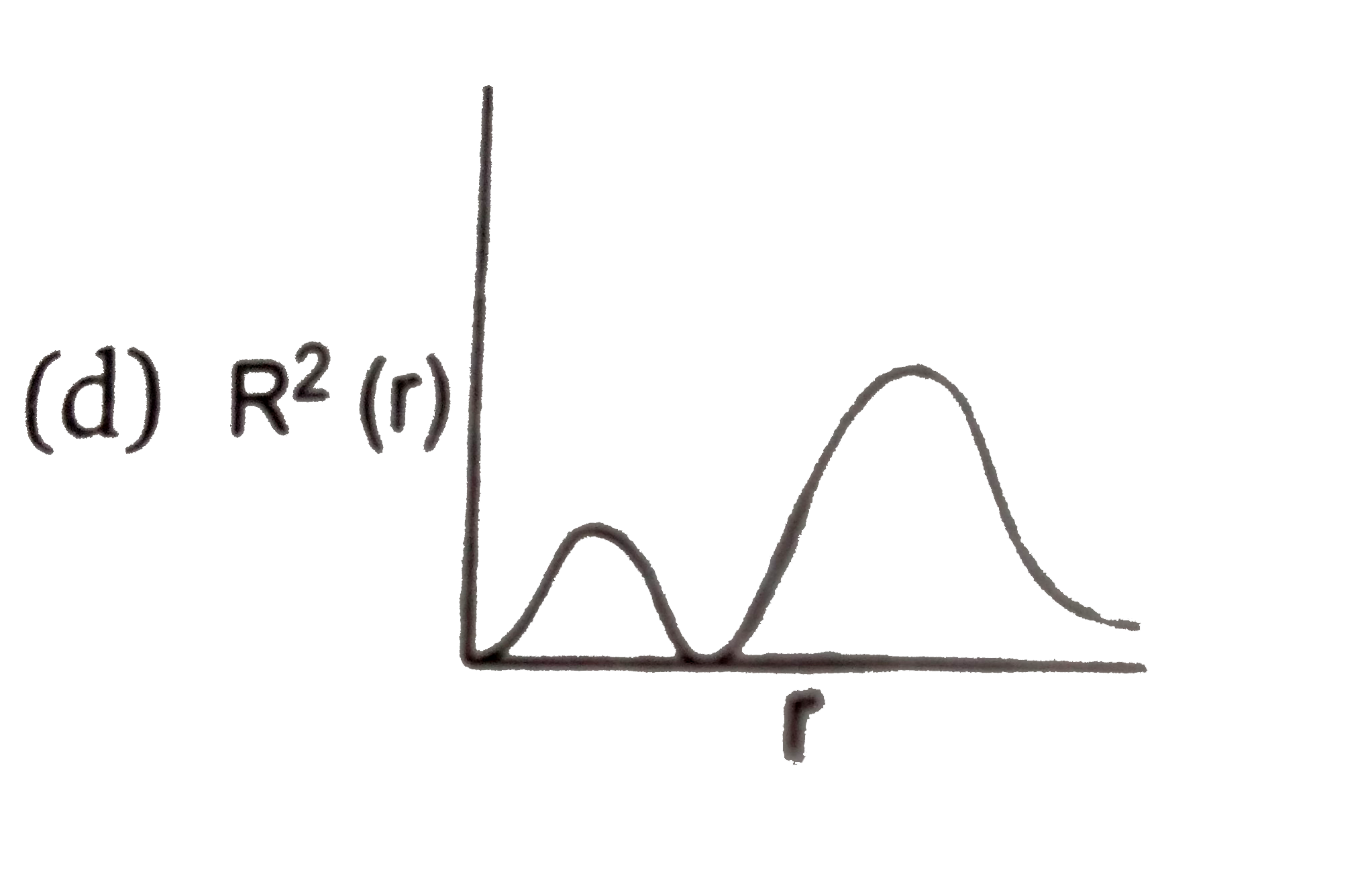
View SolutionTwo particles p and q located at distances rp and rq respectively from the centre of a rotating disc such that rp>rq.
View SolutionTwo satellites, A and B, have masses m and 2m respectively. A is in a circular orbit of radius R, and B is in a circular orbit of radius 2R around the earth. The ratio of their kinetic energies, TA/TB, is :
View Solution
