Particle A moves with 4m/s along positive Y-axis and particle B in a circle x2+y2=4 with constant angular velocity ω=2radsAt time t=0 particle is at (2m,0) Then
Magnitude of relative velocity between them at time t is (8sint)
Magnitude of relative velocity between them is maximum at t=(π4)s
Magnitude of relative velocity between them is maximum at t=(π4)s
Magnitude of relative velocity between them at time t is (8,sin2t)
The correct Answer is:A, C
Topper's Solved these Questions
Similar Questions
Assertion : A particle is under SHM along the x - axis. Its mean position is x=2, amplitude is A=2 and angular frequency ω. At t=0, particle is at origin, then x - co-ordinate versus time equation of the particle will be x=−2cosωt+2.
Reason : At t=0 , particle is at rest.
View SolutionA particle is revolving in a circular path of radius 2 m with constant angular speed 4 rad/s. The angular acceleration of particle is
View Solution
Knowledge Check
Particle A moves with 4m/s along positive y−axis and particle B in a circle x2+y2=4 (anticlockwise) with constant angular velocity ω=2rad/s. At time t=0 particle is at (2m,0). Then
Amagnitude of relative velocity between them at time t is 8sintBmagnitude of relative velocity between them is maximum at t=π4sCmagnitude of relative velocity between them is maximum at t=π2sDmagnitude of relative velocity between them at timet is 8sin2tA particle moves along a circle of radius R =1m so that its radius vector →r relative to a point on its circumference rotates with the constant angular velocity ω=2rad/s. The linear speed of the particle is
A4m/sB2m/sC1m/sD0.5m/sA particle starts moving at t = 0 in a circle of radius R=2m with constant angular acceleration of a−3rad/sec2. Initial angular speed of the particle is 1 rad/sec. At time t0 the angle between the acceleration vector and the velocity vector of the particle is 37∘.
What is the value of t0 ?A1sB12sC13sD16s
A particle is revolving in a circular path of radius 2 m with constant angular speed 4 rad/s. The angular acceleration of particle is
View SolutionCalculate the linear acceleration of a particle of a particle moving in a circle of radius 0.4 m at the instant when its angular velocity is 2 rad s−1 and its angular acceleration is 5 rad s−2.
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
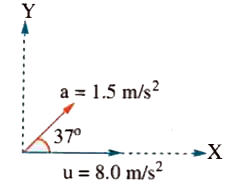
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionA particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

View SolutionA particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

View Solution
