A particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

ax=(1.5ms2)(cos370)
=(1.5ms2)×45=1.2ms2
and a_y=(1.5 m/s^2)(sin37^0)<br>=(1.5 m/s^2) xx 3/5 = 0.90 m/s^2.<br>The∈itialvelocityhascompo≠nts<br>u_x=8.0 m/s<br>andu_y=0<br>At t=0, x=0 and y=-0<br>Thex−compo≠ntofthevelocityattimet=4.0sisgivenby<br>v_x=u_x+a_xt<br>=8.0 m/s+(1.2 m/s^2)(4.0s)<br>=8.0 m/s+4.8 m/s=12.8 m/s.<br>They−compo≠tofvelocityatt=4.0sigivenby<br>v_y=u_y+a_y t<br>=0+(0.90 m/s^2)(4.0s)=3.6 m/s<br>Thevelocityofthepartic≤∗t=4.0is<br>v=sqrt(v_x^2+v_y^2)= sqrt(12.8 m/s)^2 +(3.6 m/s)^2<br>=13.3 m/s.<br>Thevelocitymakesan∠θwiththeX−aξswhere<br>tantheta= (v_y)/(v_x) = (3.6 m/s)/(12.8 m/s) = 9/32<br>Thex−c∞rdiNAteatt=4.0sis<br> x= u_x t+1/2 a_x t^2<br>=(8.0 m/s)(4.0 s)+1/2 (1.2m/s^2)(4.0s)^2<br>=32m+9.6 m 41.6m.
The y=component at t=4.0 is
y=uyt+12at2
=12(0.90ms2)(4.0s)2
=7.2m
Thus, the particle is at (41.6 m, 7.2 m) at 4.0 s.
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Worked Out Examples
20 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Short Answer
14 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
Similar Questions
The displacement x of a particle varies with time as x=4t2–15t+25. Find the position, velocity and acceleration of the particle at t = 0.
View SolutionAt t=0, the particle is at the origin and its velocity is 10m/s at an angle 37∘ with the x-axis. The particle moves in x−y plane with a constant acceleration of 1m/s2 along the y-axis. Find the magnitude and direction of the velocity after 2s.
View Solution
Knowledge Check
Vx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
 A−2.0mB+2.0mC+1.0mD−1.0m
A−2.0mB+2.0mC+1.0mD−1.0mvx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
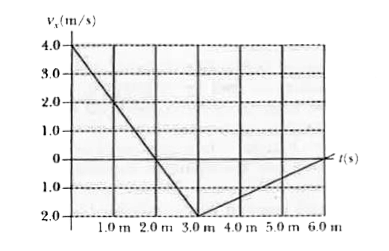 A−2.0 mB+2.0 mC+1.0 mD−1.0 m
A−2.0 mB+2.0 mC+1.0 mD−1.0 mA particle moving with a velocity equal to 0.4m/s is subjected to an acceleration of 0.15m/s2 for 2s. in a direction at the right angle to its direction of motion. The resultant velocity is
A0.7m/sB0.5m/sC0.1m/sDBetween 0.7 and 0.1m/s
A time varying force, F=2t is acting on a particle of mass 2kg moving along x-axis. velocity of the particle is 4m/s along negative x-axis at time t=0. Find the velocity of the particle at the end of 4s.
View SolutionThe acceleration of a particle varies with time t as
a=t2+t+2
where t is in seconds.
The particle starts with an initial velocity v-3m/s at t=0. find the velocity of the particle at the end of 5s.
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View SolutionA particle is moving along positive x direction and experiences a constant acceleration of 4m/s2 in negative x direction. At time t=3 second its velocity was observed to be 10m/s in positive x direction.
(a) Find the distance travelled by the particle in the interval t=0 to t=3s. Also find distance travelled in the interval t=0 to t=7.5s..
(b) Plot the displacement – time graph for the interval t=0 to 7.5s.
View SolutionAcceleration of a particle moving along the x-axis is defined by the law a=−4x, where a is in m/s2 and x is in meters. At the instant t=0, the particle passes the origin with a velocity of 2m/s moving in the positive x-direction.
(a) Find its velocity v as function of its position coordinates.
(b) find its position x as function of time t.
(c) Find the maximum distance it can go away from the origin.
View Solution
