A container contains same liquid. The container moves towards right, as shown in figure. If the liquid level makes an angle θ with horizonal plane, then
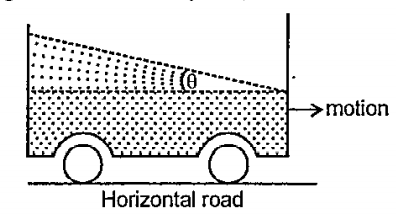
acceleration of the container is g tanθ
acceleration of the container is g cot θ
retardation of the container is g tan θ
retardation of the container is g cot θ
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One or More
A container carrying some liquid shown in the diagram is given some acceleration →a.
Aif →a is directed upwards, PA−PB increasesBif →a is directed towards right PA−PB decreasesCif →a is directed downwards, PA−PB remains same.Dif →a directed towards left PA−PB remains same. - Question 2 - Select One
A cork suspended from the bottom of a container filled with water with a string as shown in figure. If the container accelerates in a horizontal direction towards right, which one is correct?
AInclination of string with vertical is tan−1 (a/g) towards leftBInclination of the string with is tan−1 (a/g) towards rightCInclination of the string with vertical is [π/2−tan−1(a/g)] towards leftDInclination of the string with vertical is [π/2−tan−1(a/g)] towards right - Question 3 - Select One
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B isAhρgBlρaChρg−lρaDhρg+lρa
A liquid kept in a container has a horizontal acceleration 'a' as shown in figure.
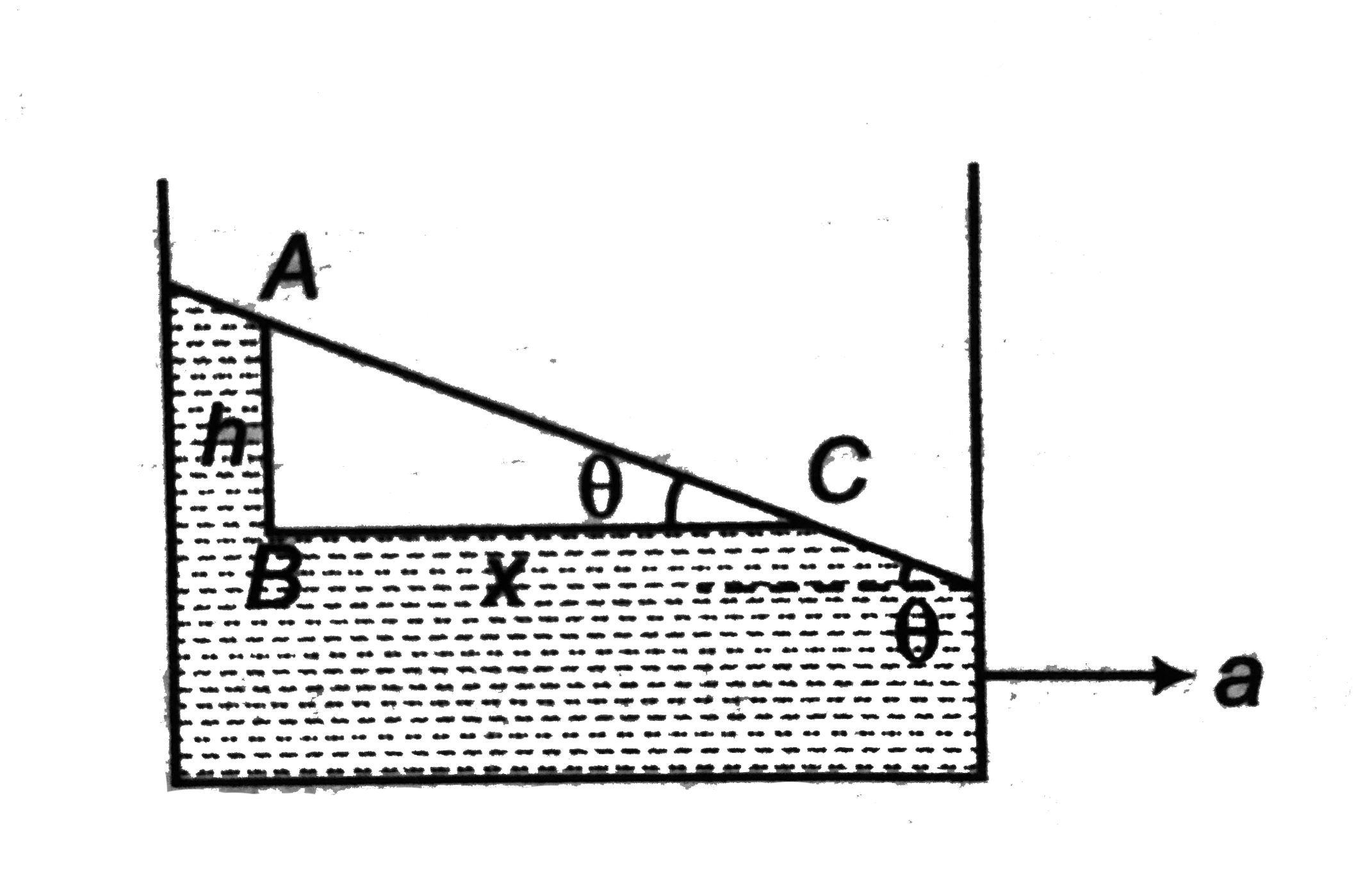
Using the pressure equation along the path ABC find the angle θ.View SolutionA liquid kept in a container has a horizontal acceleration 'a' as shown in figure.
Using the pressure equation along the path ABC find the angle θ.View Solution-
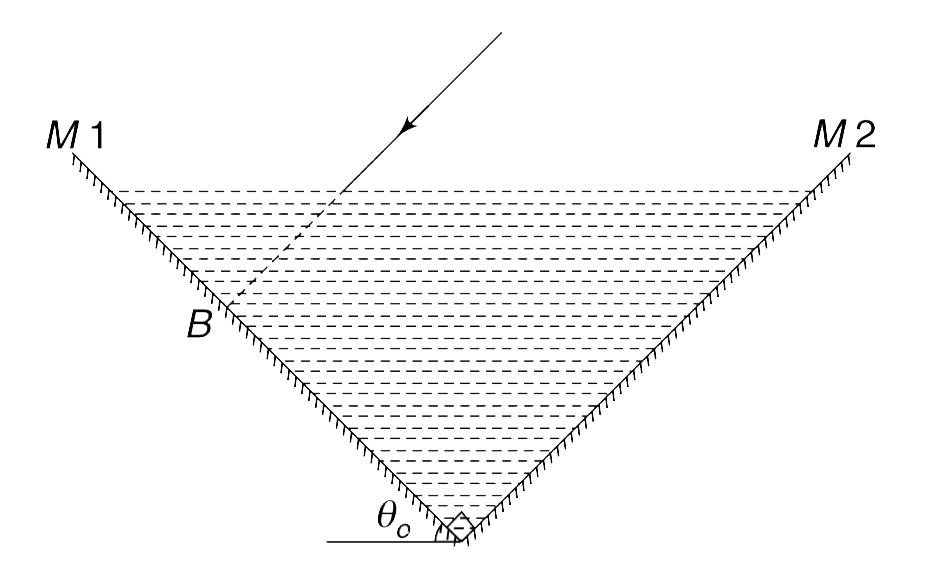
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B isView Solution Two plane mirrors M1 and M2, placed at right angles, form two sides of a container. Mirror M1 is inclined at an angle θ0 to the horizontal. A light ray AB is incident normally onM1. Now the container is filled with a liquid of refractive index μ so that the ray is first refracted, then reflected at M1. The ray is next reflected at M2 and then comes out of the liquid surface making an angle θ with the normal to the liquid surface. Find θ.
View SolutionA container made of glass (μ=1.5) contains a liquid. A ray of light passing through the liquid falls on the bottom of the container at an angle of incidence θ=tan−1(0.9) and completely polarized. The ray should strike the bottom of the container at an angle of incidences so that it undergoes total internal reflection
View Solution