If liquid level is horizontal then acceleration of container is
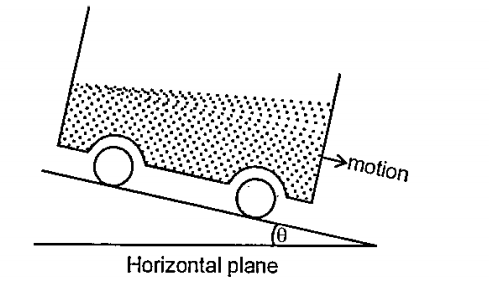
gcotθ
0
gsinθ
gtanθ
The correct Answer is:B
Topper's Solved these Questions
Similar Questions
Knowledge Check
A U-tube containing a liquid moves with a horizontal acceleration a along a direction joining the two vertical limbs. The separation between these limbs is d. The difference in their liquid levels is
Aad/gB2da/gCda/2gDdtan(a/g)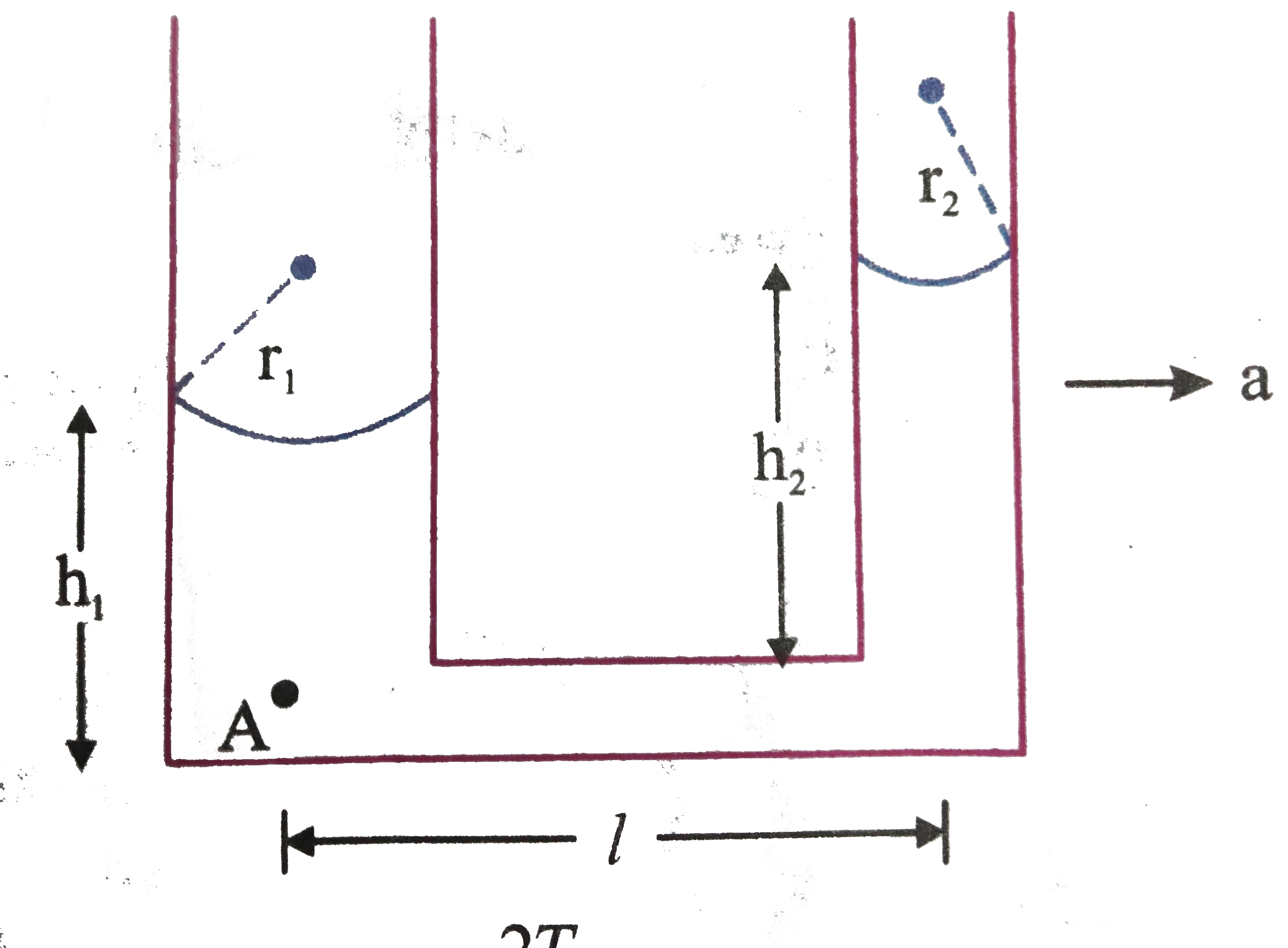
A vertical communicating tube contains a liquid of density ρ. If it moves with a horizontal acceleration a, pressure at A is equal to :Aρgh2+P0+2Tr2+ρalBρgh2+ρal+P0−2Tr2Cρgh1+P0−2Tr1Dρgh1−P0−2Tr1A sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be
 AhρgBlρgChρg−lρaDhρg−lρa
AhρgBlρgChρg−lρaDhρg−lρa
Consider a cylindrical container of cross-section area A length h and having coefficient of linear expansion αc. The container is filled by liquid of real expansion coefficient γL up to height h1. When temperature of the system is increased by Δθ then
(a). Find out the height, area and volume of cylindrical container and new volume of liquid.
(b). Find the height of liquid level when expansion of container is neglected.
(c). Find the relation between γL and αc for which volume of container above the liquid level
(i) increases
(ii). decreases
(iii). remains constant.
(d). On the surface of a cylindrical container a scale is attached for the measurement of level of liquid of liquid filled inside it. If we increase the temperature of the temperature of the system by Δθ, then
(i). Find height of liquid level as shown by the scale on the vessel. Neglect expansion of liquid.
(ii). Find the height of liquid level as shown by the scale on the vessel. Neglect expansion of container.

View SolutionConsider a cylindrical container of cross-section area A length h and having coefficient of linear expansion αc. The container is filled by liquid of real expansion coefficient γL up to height h1. When temperature of the system is increased by Δθ then
(a). Find out the height, area and volume of cylindrical container and new volume of liquid.
(b). Find the height of liquid level when expansion of container is neglected.
(c). Find the relation between γL and αc for which volume of container above the liquid level
(i) increases
(ii). decreases
(iii). remains constant.
(d). On the surface of a cylindrical container a scale is attached for the measurement of level of liquid of liquid filled inside it. If we increase the temperature of the temperature of the system by Δθ, then
(i). Find height of liquid level as shown by the scale on the vessel. Neglect expansion of liquid.
(ii). Find the height of liquid level as shown by the scale on the vessel. Neglect expansion of container.

View SolutionA L Shaped tube containing liquid of density pis accelerated horizontally with acceleration as shown in the figure. The end of tube B is closed while end A is open. If the atmospheric pressure is Po. Then the pressure at B is :
View SolutionA container shown in Fig. is accelerated horizontally with acceleration a.
a. Find the minimum value of a at which liquid just starts spilling out.

View SolutionA tank with base area L2 is filled with a liquid to height H. The tank is acceleration horizontally with acceleration a as shown in figure. If a small hole is made at the point A. then it is observed that the liquid does not come out of the tank. The magnitude of acceleration should be
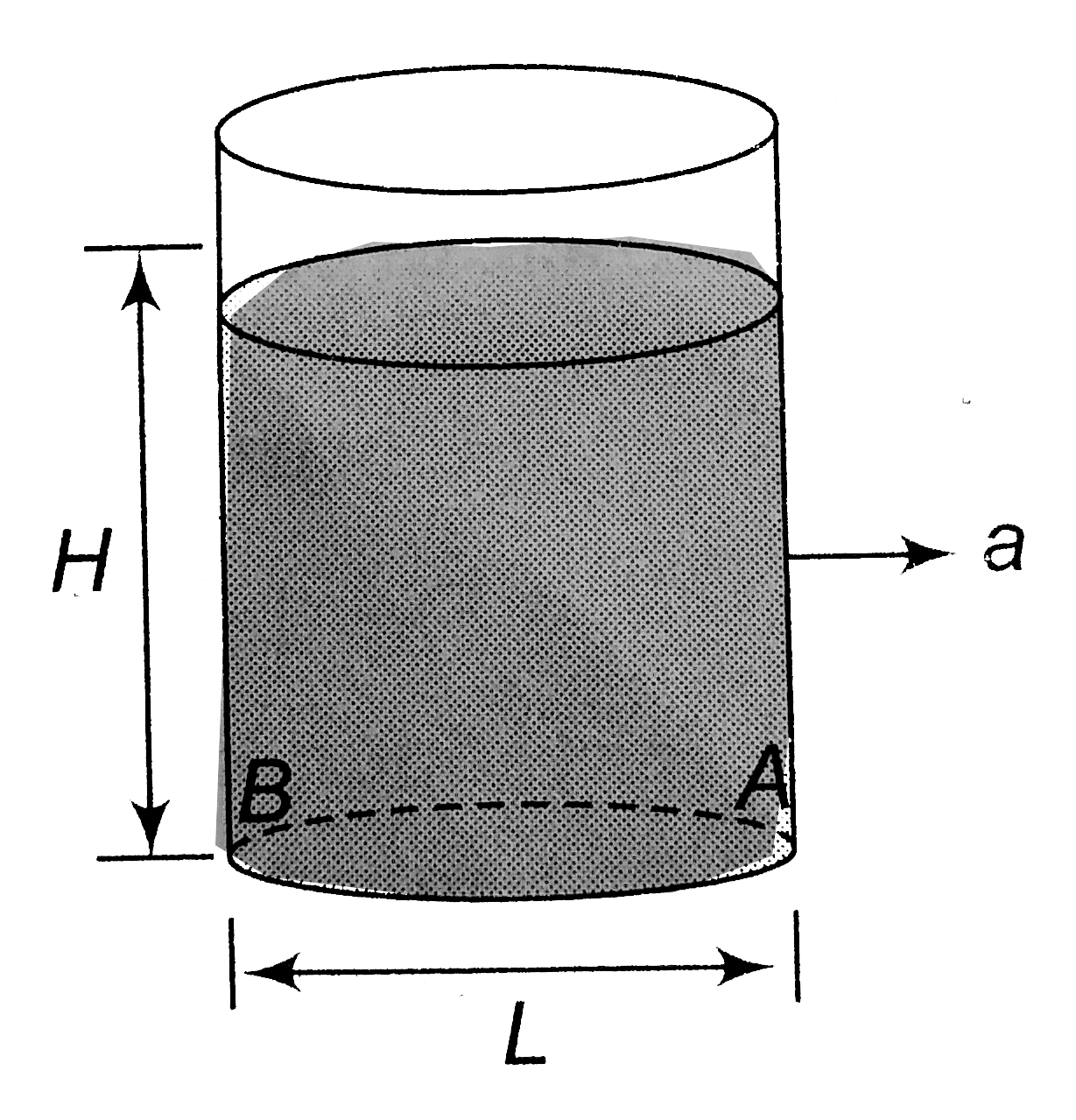
View Solution
