A liquid in beaker has temperature θ(t) at time t and q0 is temperature of surroundings, then according to Newton's law of cooling, the correct graph between loge(θ−θ0) and t is




The correct Answer is:A
Topper's Solved these Questions
Similar Questions
A liquid in a beaker has temperature θ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge(θ−θ0) and t is :
View SolutionThe correct graph between the temperature of a hot body kept in cooler surrounding and time is (Assume newton's law of cooling)
View Solution
Knowledge Check
- Question 1 - Select One
A liquid in a beaker has temperature θ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge(θ−θ0) and t is :
A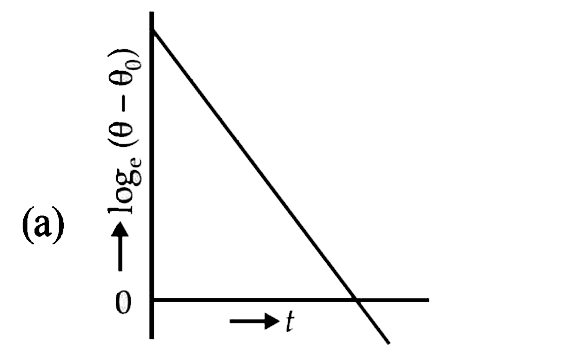 B
B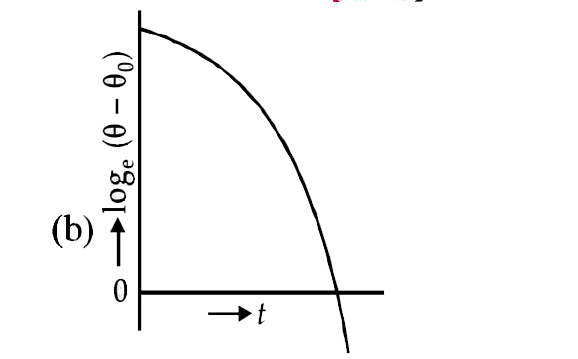 C
C D
D
- Question 2 - Select One
If the temperature of the body θ and time of cooling 't' and room temperature of the surrounding θ0. The cooling curve is
A B
B C
C D
D
- Question 3 - Select One
The correct graph between the temperature of a hot body kept in cooler surrounding and time is (Assume newton's law of cooling)
A B
B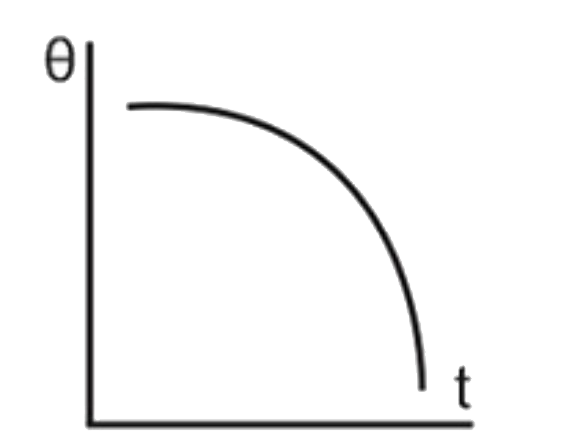 C
C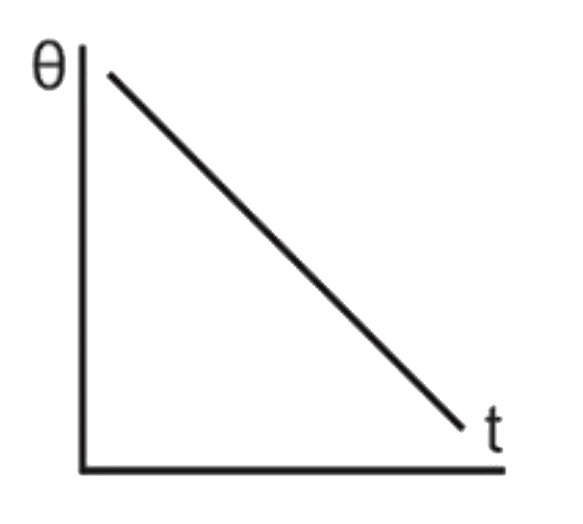 D
D
In Newton's law of cooling dθdt=−k(θ−θ0) the constant k is proportional to .
View SolutionThe temperature of water in calorimeter is θ and the temperature of surrounding is θ0(<θ). Observation are recorded for temperature difference (θ−θ0) and time t. The cooling curve is best represented in graph.
View SolutionThemperature of a body θ is slightly more than the temperature of the surrounding θ0 its rate of cooling (R) versus temperature of body (θ) is plotted its shape would be .
View SolutionIn Newton's law of cooling dθdt=−k(θ−θ0) the constant k is proportional to .
View SolutionThemperature of a body θ is slightly more than the temperature of the surrounding θ0 its rate of cooling (R) versus temperature of body (θ) is plotted its shape would be .
View Solution

