The correct graph between the temperature of a hot body kept in cooler surrounding and time is (Assume newton's law of cooling)

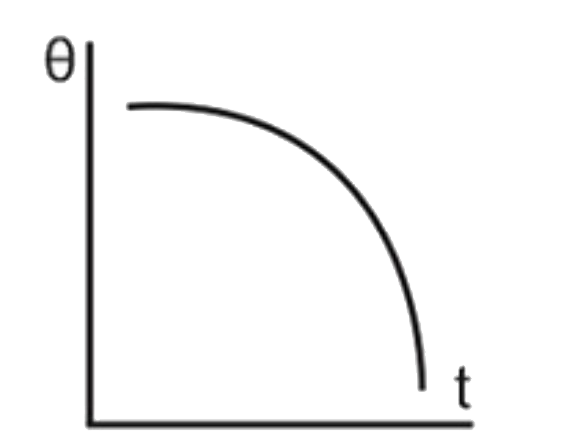
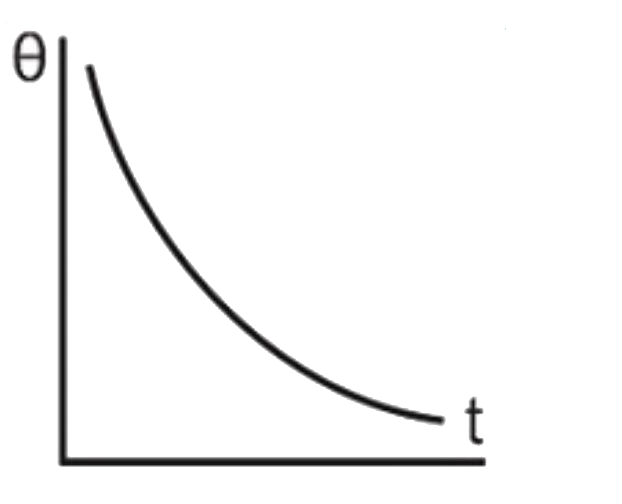
The correct Answer is:D
To solve the problem regarding the correct graph between the temperature of a hot body kept in cooler surroundings over time, we will use Newton's Law of Cooling. Here’s a step-by-step solution:
Step 1: Understand Newton's Law of Cooling
Newton's Law of Cooling states that the rate of change of temperature of an object is proportional to the difference between its own temperature and the ambient temperature. Mathematically, it can be expressed as:
dTdt=−k(T−Ts)
where:
- T is the temperature of the hot body,
- Ts is the surrounding temperature,
- k is a positive constant,
- t is time.
Step 2: Set Initial Conditions
Let’s assume:
- The initial temperature of the hot body is T0 (where T0>Ts).
- At time t=0, the temperature of the body is T0.
Step 3: Solve the Differential Equation
To find the temperature of the body at any time t, we can integrate the equation. The solution to the differential equation is given by:
T(t)=Ts+(T0−Ts)e−kt
Step 4: Analyze the Temperature Over Time
1. At t=0:
T(0)=Ts+(T0−Ts)e0=T0
This confirms that the initial temperature is T0.
2. As t→∞:
T(t)→Ts+(T0−Ts)e−∞=Ts
This indicates that the temperature of the body approaches the surrounding temperature Ts as time progresses.
Step 5: Determine the Graph Shape
The equation T(t)=Ts+(T0−Ts)e−kt shows that the temperature decreases exponentially over time. The graph of this function will start at T0 and asymptotically approach Ts as t increases.
Conclusion
The correct graph representing the temperature of a hot body cooling in a cooler surrounding over time will be an exponential decay curve starting from T0 and approaching Ts.
Newton's Law of Cooling states that the rate of change of temperature of an object is proportional to the difference between its own temperature and the ambient temperature. Mathematically, it can be expressed as:
- T is the temperature of the hot body,
- Ts is the surrounding temperature,
- k is a positive constant,
- t is time.
Let’s assume:
- The initial temperature of the hot body is T0 (where T0>Ts).
- At time t=0, the temperature of the body is T0.
To find the temperature of the body at any time t, we can integrate the equation. The solution to the differential equation is given by:
1. At t=0:
T(0)=Ts+(T0−Ts)e0=T0
This confirms that the initial temperature is T0.
T(t)→Ts+(T0−Ts)e−∞=Ts
This indicates that the temperature of the body approaches the surrounding temperature Ts as time progresses.
The equation T(t)=Ts+(T0−Ts)e−kt shows that the temperature decreases exponentially over time. The graph of this function will start at T0 and asymptotically approach Ts as t increases.
The correct graph representing the temperature of a hot body cooling in a cooler surrounding over time will be an exponential decay curve starting from T0 and approaching Ts.
Similar Questions
A cooling curve is plotted between the temperature of a hot body and time. Which of the following is not true for the cooling curve?
View SolutionA liquid in a beaker has temperature θ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge(θ−θ0) and t is :
View SolutionA body cools from 60∘C to 50∘C in 10 min. Find its temperature at the end of next 10 min if the room temperature is 25∘C. Assume Newton's law of cooling holds.
View SolutionA metal ball of mass 1 kg is heated by means of a 20 W heater in a room at 20∘C. The temperature of the ball becomes steady at 50∘C. Assume newton's law of cooling to hold good in the given situation. The temperature of the ball rises uniformly from 20∘C to 30∘C in 5 minutes. select the correct alternatives
(1) The rate of heat loss by ball to surrounding is 20 W, when it is at 50∘
(2) The rate of heat loss by ball to surrounding is 203W, when it is at 30∘C
(3) The rate of heat loss by ball to surrounding 20 W, when it is at 30∘C
(4). The specific heat capacity of the gas is 500 J/kg K.
View SolutionA metal block is placed in a room which is at 10∘C for long time. Now it is heated by an electric heater of power 500 W till its temperature becomes 50∘C. Its initial rate of rise of temperature is 2.5∘C/sec. The heater is switched off and now a heater of 100W is required to maintain the temperature of the block at 50∘C . (Assume Newtons Law of cooling to be valid)
What is the rate of cooling of block at 50∘C if the 100W heater is also switched off?
View SolutionWhat is the difference between Stefan's law and Newton's law of cooling ?
View SolutionConsider a solid sphere placed in surrounding with small temperature difference between sphere's surface and surrounding. If ΔT and r represent temperature difference (between sphere and surrounding) and radius of sphere respectively, rate of cooling of the sphere is directly proportional to:
View SolutionThe graph between the separation of the slits and fringe width in Young.s double slit experiment is (assume that the distance between the source and the screen and the wavelength of the source are kept constant)
View SolutionAccording to Newton’s law of cooling, the rate of cooling of a body is proportional to (Δθ)n , where Δθis the difference of the temperature of the body and the surrounding, and n is equal to :
View SolutionA body cools in a surrounding of constant temperature 30∘C. Its heat capacity is 2J/∘C. Initial temperature of the body is 40∘C. Assume Newton's law of cooling is valid. The body cools to 36∘C in 10 minutes.
In further 10 minutes it will cool from 36∘C to :
View Solution
