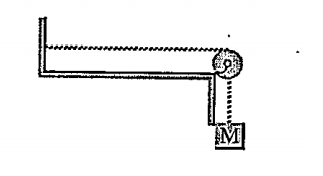
A string of length 1 m fixed at one end and on the other end a block of mass M =4 kg is suspended. The string is set into vibrations and represented by equation y=6sin $(\frac{π x}{10}) . cos 100 π t$ where x and y are in cm and t in seconds.

Write down the equations of the component waves whose superposition gives the wave.

Text Solution

Verified by Experts

$y_{1} = 3 sin (\frac{π x}{10} - 100 π t) and y_{2} = 3 sin (\frac{π x}{10} + 100 π t)$

|

Updated on:21/07/2023

Class 11 PHYSICS WAVE MOTION AND SOUND -I & II

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
The vibrations of a string of length $600 c m$ fixed at both ends are represented by the equation $y = 4 sin (π \frac{x}{15}) cos (96 π t)$
where $x$ and $y$ are in $c m$ and $t$ in seconds.
AThe maximum displacement of a particle at $x = 5 c m$ is $2 \sqrt{3} c m$ .
BThe nodes located along the string are $15 n$ where ineger $n$ varies from 0 to 40.
CThe velocity of the particle at $x = 7.5 c m$ at $t = 0.25 sec$ is zero
DThe equations of the component waves whose superpostion gives the above wave are $2 sin 2 π (\frac{x}{30} + 48 t), 2 sin 2 π (\frac{x}{30} - 48 t)$
Question 2 - Select One
The length of a sonometer wire is $90 c m$ and the stationary wave setup in the wire is represented by an equation $y = 6 sin (\frac{π x}{30}) cos (250 t)$ where $x$ , $y$ are in cm and $t$ is in second. The number of loops is
A $1$
B $2$
C $4$
D $3$
Question 3 - Select One
The vibrations of a string of length 60 cm fixed at both ends are represented by the equation
$y = 4 sin (π x / 15) cos (96 π t)$
where x and y are in cm and t in seconds. The maximum displacement at x = 5 cm is–
A $2 \sqrt{3} c m$
B $3 \sqrt{2} c m$
C $\sqrt{2} c m$
D $\sqrt{3} c m$

PATHFINDER-WAVE MOTION AND SOUND -I & II-QUESTION BANK

Home
Ask Doubt
Profile