Two wires 1 and 2 of the same cross -sectional area A=10mm2 and the same length but made of different materials are welded together and their ends are rigidly clamped between two walls, as shown in the figure. The respective Young's Moduli and the linear coefficients of thermal are :
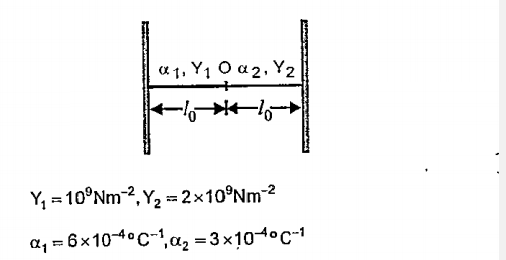
(A) If the temperature of the system is reduced by 20∘C,then
(i)find the tension in each wire
(ii)Find the displacement of the joint O
(i) 120 N (ii) zero
Topper's Solved these Questions
Similar Questions
Two wires 1 and 2 of the same cross sectional area A=10mm2 and the same length but made of different materials are welded together and their ends are rigidly clamped between two walls, as shown in figure. The respective young's moduli and coefficient of linear expansions are y1=109N/m2,y2=2×109N/m2,α1=6×10−4∘C−1,α2=3×10−4∘C−1 . if temperature of system reduced by 20∘C then

Find the displacement of the joint
View SolutionTwo wires A and B have the same cross section and are made of the same material, but the length of wire A is twice that of B. Then, for a given load
View Solution
Knowledge Check
Two wires A and B have the same cross section and are made of the same material, but the length of wire A is twice that of B. Then, for a given load
Athe extension of A will be twice that of BBthe extensions of A and B will be equalCthe strain in A will be half that in BDthe strains in A and B will be equalTwo wires of the same material and same cross sectional area are vibrating with the same frequency. The first wire of length 80 cm is loaded with 8 kg and the second wire is loaded with 2 kg. The length of the second wire is
A40cmB80cmC70cmD60cmTwo rods of different materials are clamped at their ends rigidy. When they are heated for the same rise in temperature, same thermal stresses are prouded in them. If their Young's modulll are in the ratio x:y then ratio fo coefficients of their linear expanison is
Ax:yBy:xCx2:y2Dy2:x2
A metal bar of length L and area of cross-section A is rigidly champed between two walls. The Young's modulus of its material is Y and the coefficient of linear expansion is α. The bar is heated so that its temperature is increased by θ∘C. Find the force exerted at the ends of the bar.
View SolutionTwo wires of the same material and same length have radii 1 mm and 2 mm respectively. Compare :
their resistances,
View SolutionTwo bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is

View SolutionTwo bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is

View SolutionA wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
View Solution
