Two light vertical springs 1 and 2 of stifiness k and 2k are connected to a light horizontal rod at its two ends as shown. A bead of chewing gam of mass 'm' is sticked gently at the mid point of the rod and lowcred slowly, such that where equilibrium is reached the bead displaced by x0. The period of SHM of the bead is 2π√pnqK, Find |p−q|.
'(##CEN_KSR_PHY_JEE_C16_E01_032_Q16##)'
The correct Answer is:5
Topper's Solved these Questions
Similar Questions
Two masses m1 and m2 are connected by a light rod of length I. If rod is rotating about an axis with angular speed Ω. Such that its kinetic energy is minimum then its K.E. is
View SolutionTwo small beads having positive charges 3q and q are fixed at the opposite ends of a horizontal, insulating rod, extending from the origin to the point x=d as shown in fig. A third small charged bead is free to slide on the rod. At what position is the third bead in equilibrium? Can it be in stable equilibrium ?
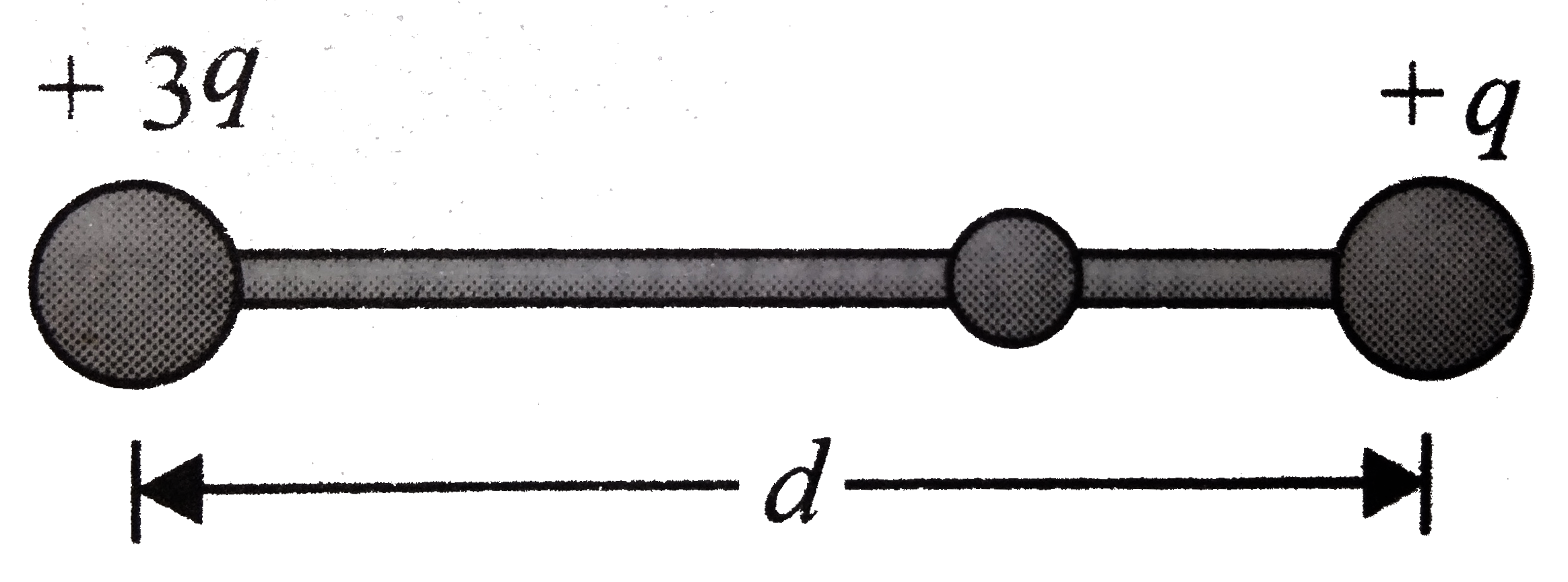
View Solution
Knowledge Check
Two light verticle springs 1 and 2 of stiffness K and 2K are connected by a 1 light horizontal rod. A bead of chewing gum of mass 'm' is placed gently at the mid point of the rod and lowered slowly.
The period of SHM of the bead isA2π√3m8KB2π√m3KC3π√2mKDNone of theseTwo light verticle springs 1 and 2 of stiffness K and 2K are connected by a 1 light horizontal rod. A bead of chewing gum of mass 'm' is placed gently at the mid point of the rod and lowered slowly.
The energy of oscillation of the bead for an amplitude y0 is equal to (x0=maximum displacement of the bead in the process of lowering)Amgx0Bmg(x0+y0)C32Ky20D43Ky20Two light verticle springs 1 and 2 of stiffness K and 2K are connected by a 1 light horizontal rod. A bead of chewing gum of mass 'm' is placed gently at the mid point of the rod and lowered slowly.
The ratio of magnitude of work done by the external agent to that by gravity in lowering the bead till it remains at rest isA1:1B1:2C2:1D1:4
Two small beads having positive charges 3q and q are fixed at the opposite ends of a horizontal, insulating rod, extending from the origein to the point x=d as shown in fig. A third small charged bead is free to slide on the rod. At what position is the third bead in equilibrium? Can it be in stable eqyilibrium ?

View SolutionA horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is
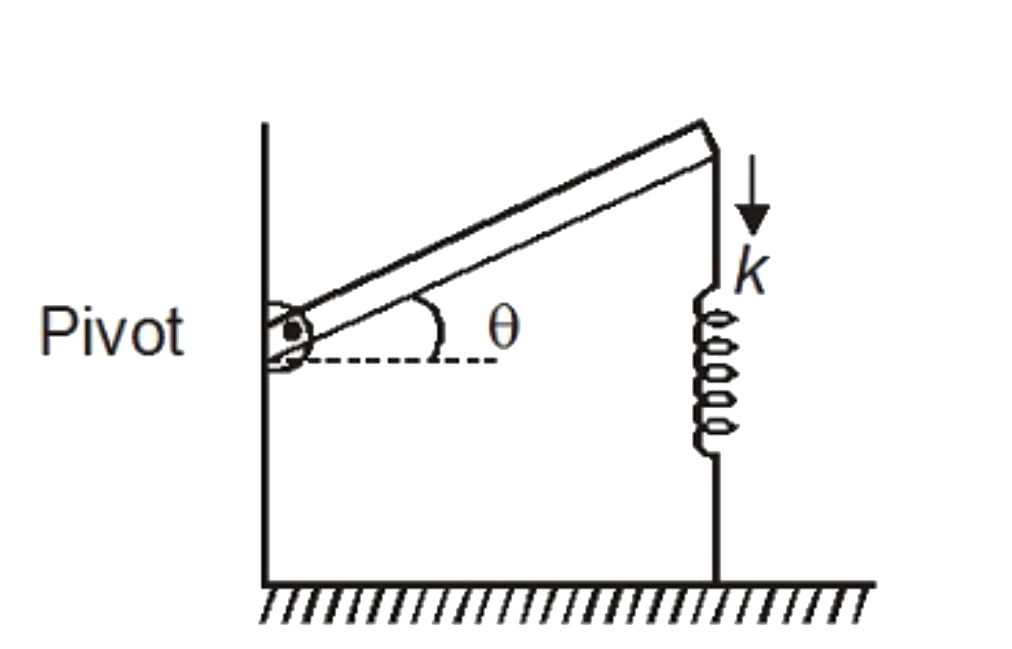
View SolutionA horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is

View SolutionTwo light vertical springs with equal natural length and spring constants k1 and k2 are separated by a distancel. Their upper end the ends A and B of a light horizontal rod AB. A vertical downwards force F is applied at point C on the rod. AB will remain horizontal in equilibrium if the distance AC is
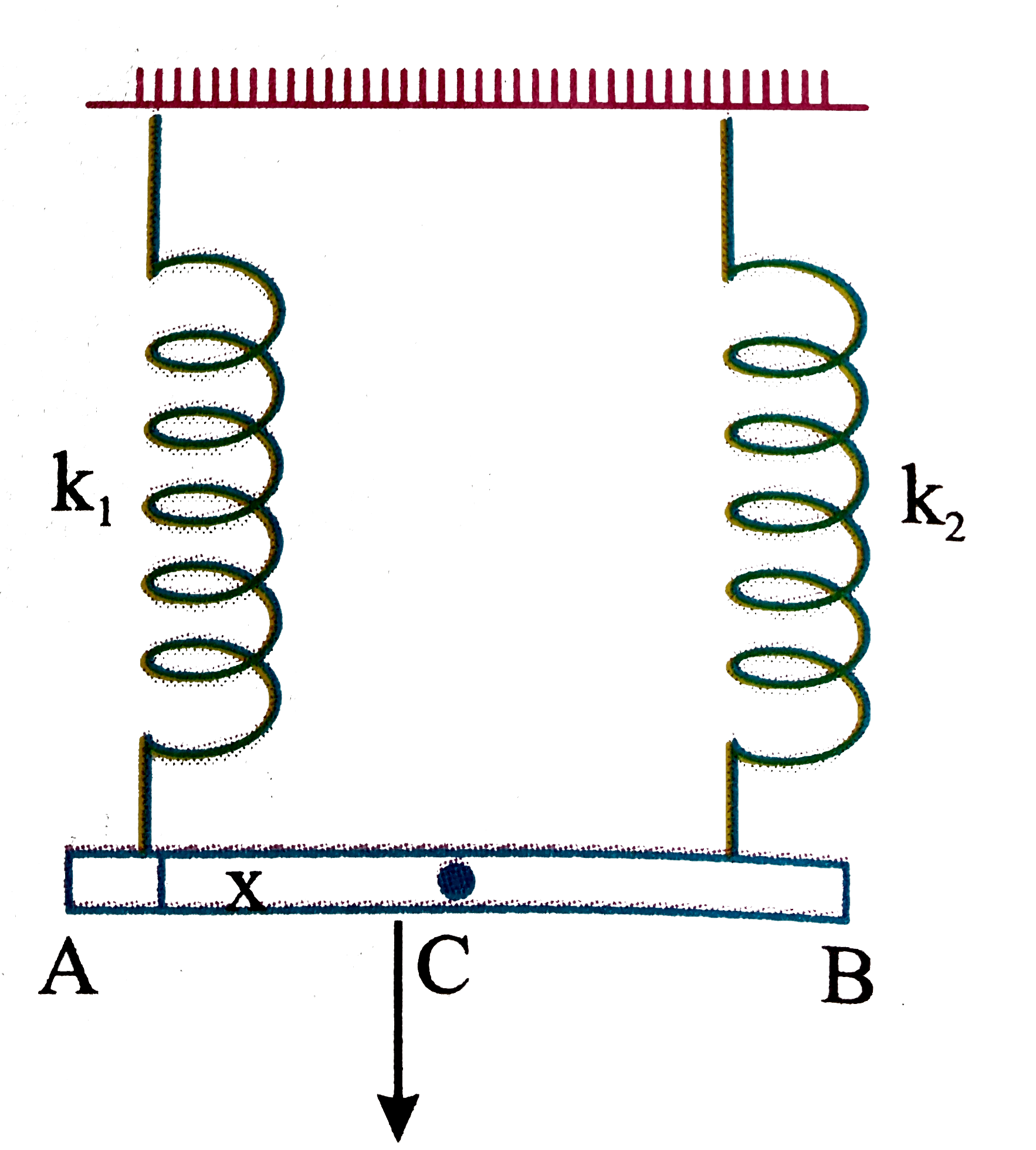
View SolutionA bead of mass 5 kg is free to slide on the horizontal rod AB. They are connected to two identical springs of natural length h ms. As shown. If initially bead was at O & M is vertically below L then, velocity of bead at point N will be :

View Solution
