Two masses and are connected by a light rod of length I. If rod is rotating about an axis with angular speed . Such that its kinetic energy is minimum then its K.E. is
To solve the problem, we need to find the kinetic energy of a system consisting of two masses m1 and m2 connected by a light rod of length L, rotating about an axis with angular speed Ω such that its kinetic energy is minimized. Here's a step-by-step solution:
Step 1: Understand the Moment of Inertia
The moment of inertia I of the system is given by the formula:
I=m1x2+m2(L−x)2
where x is the distance from the axis of rotation to mass m1.
Step 2: Differentiate the Moment of Inertia
To minimize the kinetic energy, we need to minimize the moment of inertia I. We differentiate I with respect to x and set the derivative equal to zero:
dIdx=2m1x−2m2(L−x)=0
Step 3: Solve for x
Rearranging the equation gives:
2m1x=2m2(L−x)
m1x+m2x=m2L
x(m1+m2)=m2L
Thus, we find:
x=m2Lm1+m2
Step 4: Substitute x Back into the Moment of Inertia
Now we substitute x back into the moment of inertia equation:
I=m1(m2Lm1+m2)2+m2(L−m2Lm1+m2)2
Calculating L−x:
L−x=L−m2Lm1+m2=m1Lm1+m2
Now substituting this into the moment of inertia:
I=m1(m2Lm1+m2)2+m2(m1Lm1+m2)2
=m1m22L2(m1+m2)2+m2m21L2(m1+m2)2
=L2(m1m22+m2m21)(m1+m2)2
=L2m1m2(m1+m2)(m1+m2)2
Step 5: Calculate the Kinetic Energy
The kinetic energy K.E. of the system is given by:
K.E.=12IΩ2
Substituting I into the kinetic energy equation:
K.E.=12(L2m1m2(m1+m2)(m1+m2)2)Ω2
=12L2m1m2Ω2(m1+m2)
Final Answer
Thus, the minimum kinetic energy of the system is:
K.E.=12m1m2L2Ω2m1+m2
The moment of inertia I of the system is given by the formula:
I=m1x2+m2(L−x)2
where x is the distance from the axis of rotation to mass m1.
To minimize the kinetic energy, we need to minimize the moment of inertia I. We differentiate I with respect to x and set the derivative equal to zero:
dIdx=2m1x−2m2(L−x)=0
Rearranging the equation gives:
2m1x=2m2(L−x)
m1x+m2x=m2L
x(m1+m2)=m2L
Thus, we find:
x=m2Lm1+m2
Now we substitute x back into the moment of inertia equation:
I=m1(m2Lm1+m2)2+m2(L−m2Lm1+m2)2
Calculating L−x:
L−x=L−m2Lm1+m2=m1Lm1+m2
Now substituting this into the moment of inertia:
I=m1(m2Lm1+m2)2+m2(m1Lm1+m2)2
=m1m22L2(m1+m2)2+m2m21L2(m1+m2)2
=L2(m1m22+m2m21)(m1+m2)2
=L2m1m2(m1+m2)(m1+m2)2
The kinetic energy K.E. of the system is given by:
K.E.=12IΩ2
Substituting I into the kinetic energy equation:
K.E.=12(L2m1m2(m1+m2)(m1+m2)2)Ω2
=12L2m1m2Ω2(m1+m2)
Thus, the minimum kinetic energy of the system is:
K.E.=12m1m2L2Ω2m1+m2
Topper's Solved these Questions
Similar Questions
Two particles of masses m1andm2 are joined by a light rigid rod of length r. The system rotates at an angular speed ω about an axis through the centre of mass of the system and perpendicular to the rod. Show that the angular momentum of the system is L=μr2ω where μ is the reduced mass of the system defined as μ=m1m2m1+m2
View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2
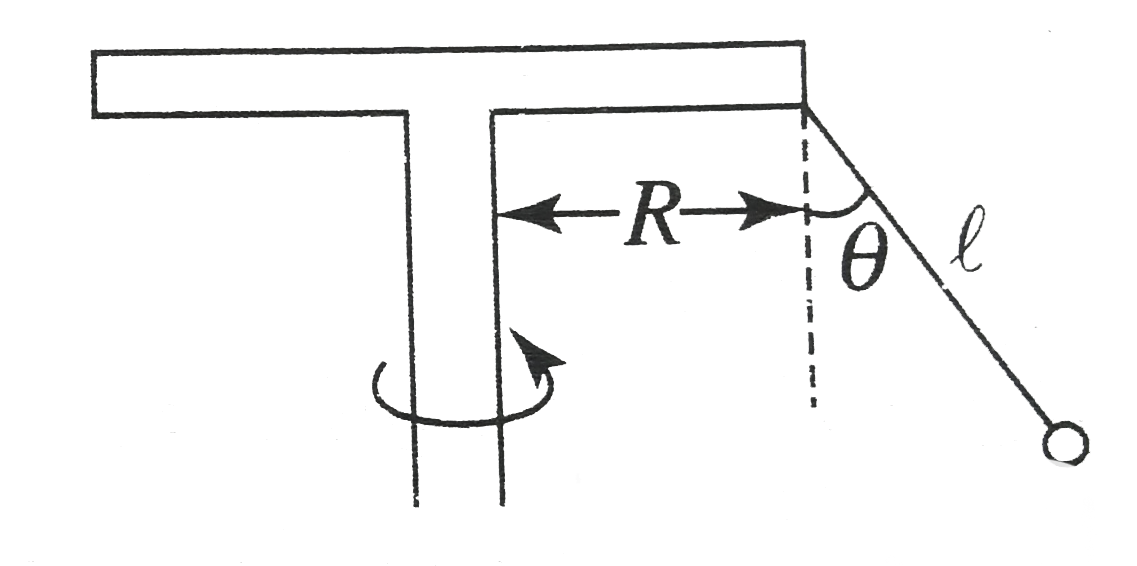
A pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. angular speed ω
View SolutionA rod of mass m and length l is connected with a light rod of length l. The composite rod is made to rotate with angular velocity ω as shown in the figure. Find the
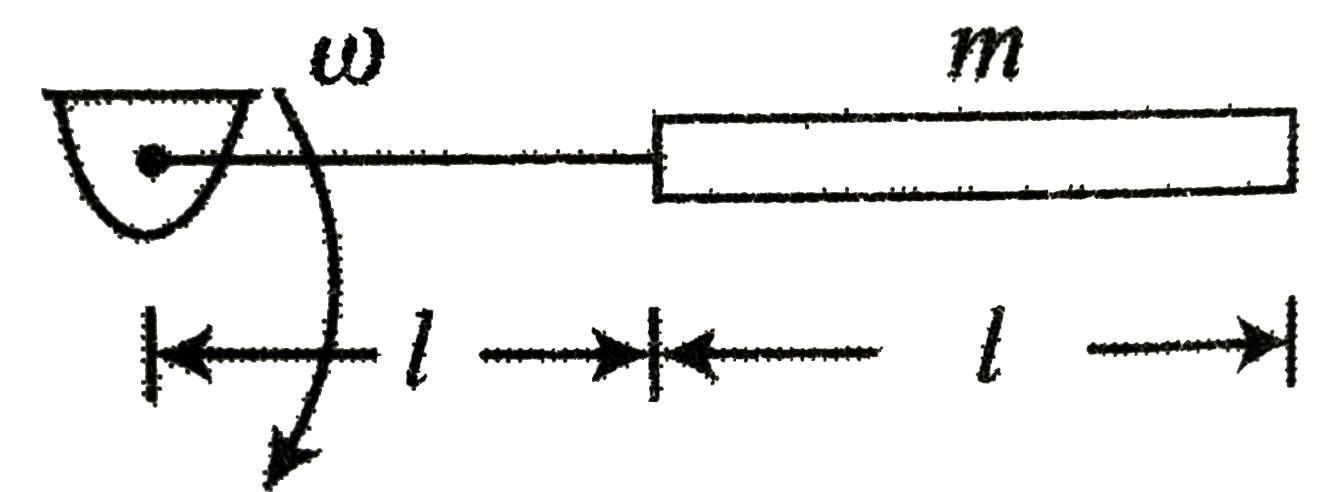
a. translational kinetic energy.
b. rotational kinetic energy.
c. total kinetic energy of rod.
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.

View SolutionTwo point masses m1 and m2 are joined by a weightless rod of length r. Calculate the moment of inerrtia of the system about an axis passing through its centre of mass and perpendicular to the rod.
View SolutionTwo point masses m and 4m are connected by a light rigid rod of length l at the opposite ends. Moment of inertia of the system about an axis perpendicular to the length and passing through the centre of mass is
View Solution
