A particle is moving along x-axis under the action of force, F which varies with its position as F∝14√x. Find the variation of power due to this fore with x.
To solve the problem step by step, we will follow the reasoning laid out in the video transcript.
Step 1: Express the Force
We start with the given relationship for the force F:
F∝14√x⟹F=k4√x=kx−1/2
where k is a constant of proportionality.
Hint: Remember that "proportional to" can be converted into an equation by introducing a constant.
Step 2: Relate Force to Acceleration
Using Newton's second law, we know that:
F=ma⟹a=Fm
Substituting the expression for F:
a=kx−1/2m=kmx−1/2
Let k′=km, then:
a∝x−1/2
Hint: Acceleration can be expressed in terms of the derivative of velocity with respect to time.
Step 3: Express Acceleration in Terms of Velocity
We know that:
a=dvdt=dvdx⋅dxdt=vdvdx
Setting this equal to our expression for acceleration:
vdvdx=k′x−1/2
Hint: This equation relates the change in velocity to the position of the particle.
Step 4: Separate Variables and Integrate
Rearranging gives:
vdv=k′x−1/2dx
Now, we integrate both sides:
∫vdv=∫k′x−1/2dx
This results in:
v22=k′⋅2x1/2+C
where C is the constant of integration.
Hint: Remember to apply the correct integration rules for power functions.
Step 5: Solve for Velocity
From the integration, we can express v2:
v2=4k′x1/2+2C
Assuming C=0 for simplicity, we have:
v2∝x1/2⟹v∝x1/4
Hint: The relationship between velocity and position can often be simplified by assuming initial conditions.
Step 6: Calculate Power
Power P is given by:
P=F⋅v
Substituting our expressions for F and v:
P∝(kx−1/2)⋅(x1/4)=kx−1/2x1/4=kx−1/4
Hint: Power is the product of force and velocity, so ensure both are expressed in terms of the same variable.
Step 7: Final Expression for Power
Thus, we find:
P∝x−1/4
Hint: The final relationship shows how power varies with position x.
Conclusion
The variation of power due to the force with respect to x is:
P∝x−1/4
We start with the given relationship for the force F:
F∝14√x⟹F=k4√x=kx−1/2
where k is a constant of proportionality.
Using Newton's second law, we know that:
F=ma⟹a=Fm
Substituting the expression for F:
a=kx−1/2m=kmx−1/2
Let k′=km, then:
a∝x−1/2
We know that:
a=dvdt=dvdx⋅dxdt=vdvdx
Setting this equal to our expression for acceleration:
vdvdx=k′x−1/2
Rearranging gives:
vdv=k′x−1/2dx
Now, we integrate both sides:
∫vdv=∫k′x−1/2dx
This results in:
v22=k′⋅2x1/2+C
where C is the constant of integration.
From the integration, we can express v2:
v2=4k′x1/2+2C
Assuming C=0 for simplicity, we have:
v2∝x1/2⟹v∝x1/4
Power P is given by:
P=F⋅v
Substituting our expressions for F and v:
P∝(kx−1/2)⋅(x1/4)=kx−1/2x1/4=kx−1/4
Thus, we find:
P∝x−1/4
The variation of power due to the force with respect to x is:
P∝x−1/4
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION
2 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF
95 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A particle is moving along x-axis under the action of a force F, which varies with its position (x)asF∝1√x.Find the variation of power due to this force with x.
View SolutionA particle is moving along x-axis under the action of a force, F which varies with its position (x) as F∝x−1/4. The variation of power due to this force with x is
View SolutionA particle starts moving from rest along y axis and a variable force F acts on it such that F∞y−15 (y>0). The variation of power P of this force with y is given as
View SolutionA particle is moving along x-axis. Its velocity v with x co-ordinate is varying as v=√x. Then
View SolutionA 4kg particle is moving along the x- axis under the action of the force F=−(π216)xN At t=2sec the particle passes through the origin and t=10sec, the speed is 4√2m/s The amplitude of the motion is
View SolutionA particle of mass m moves from rest under the action of a constant force F which acts for two seconds. The maximum power attained is
View SolutionA particle is moving along the x-axis and its position-time graph is shown. Determine the sign of acceleration.
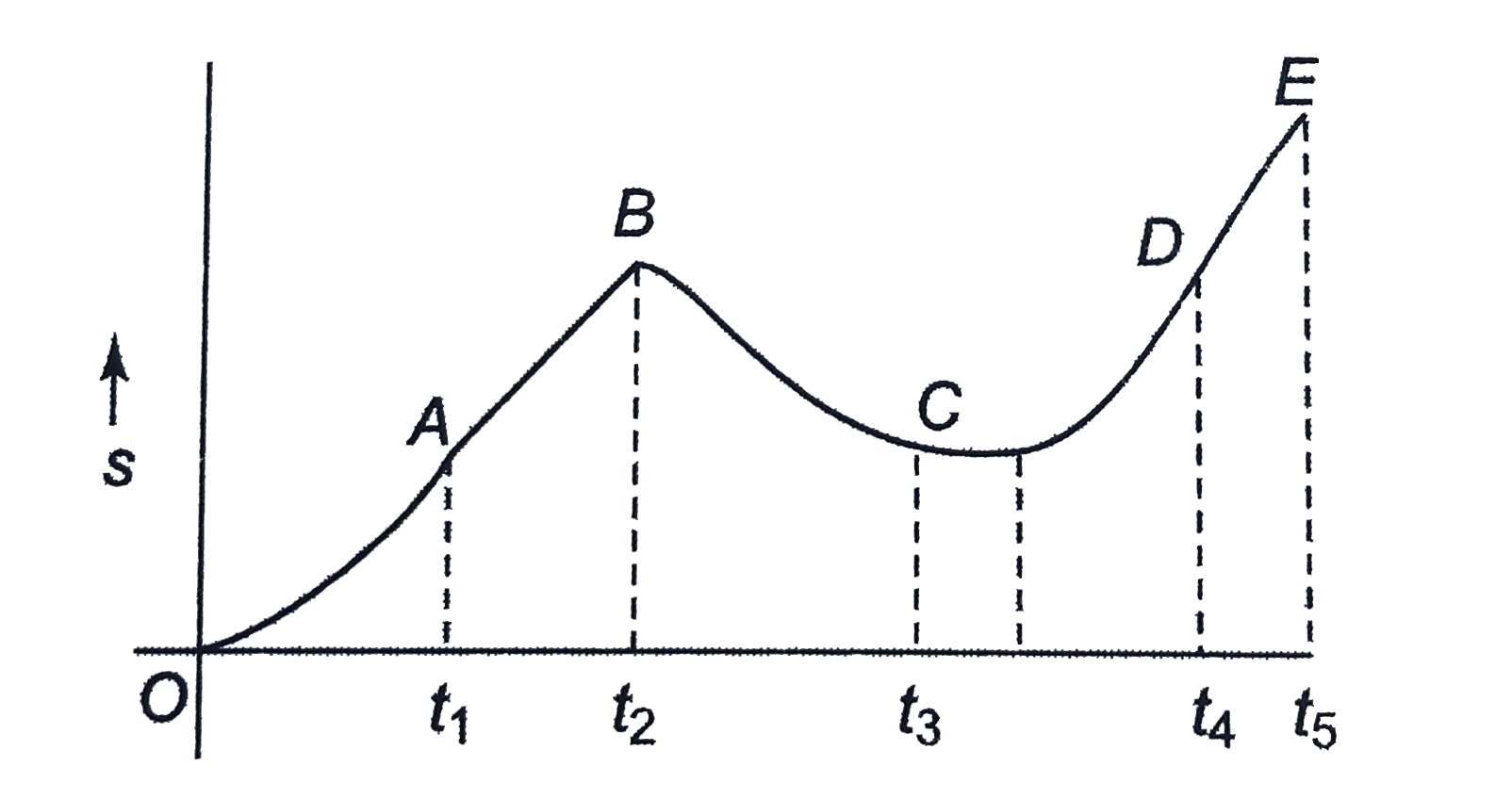
View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View SolutionFor a particle moving under the action of a variable force, kinetic energy (k) varsus position (x) graph is given, then
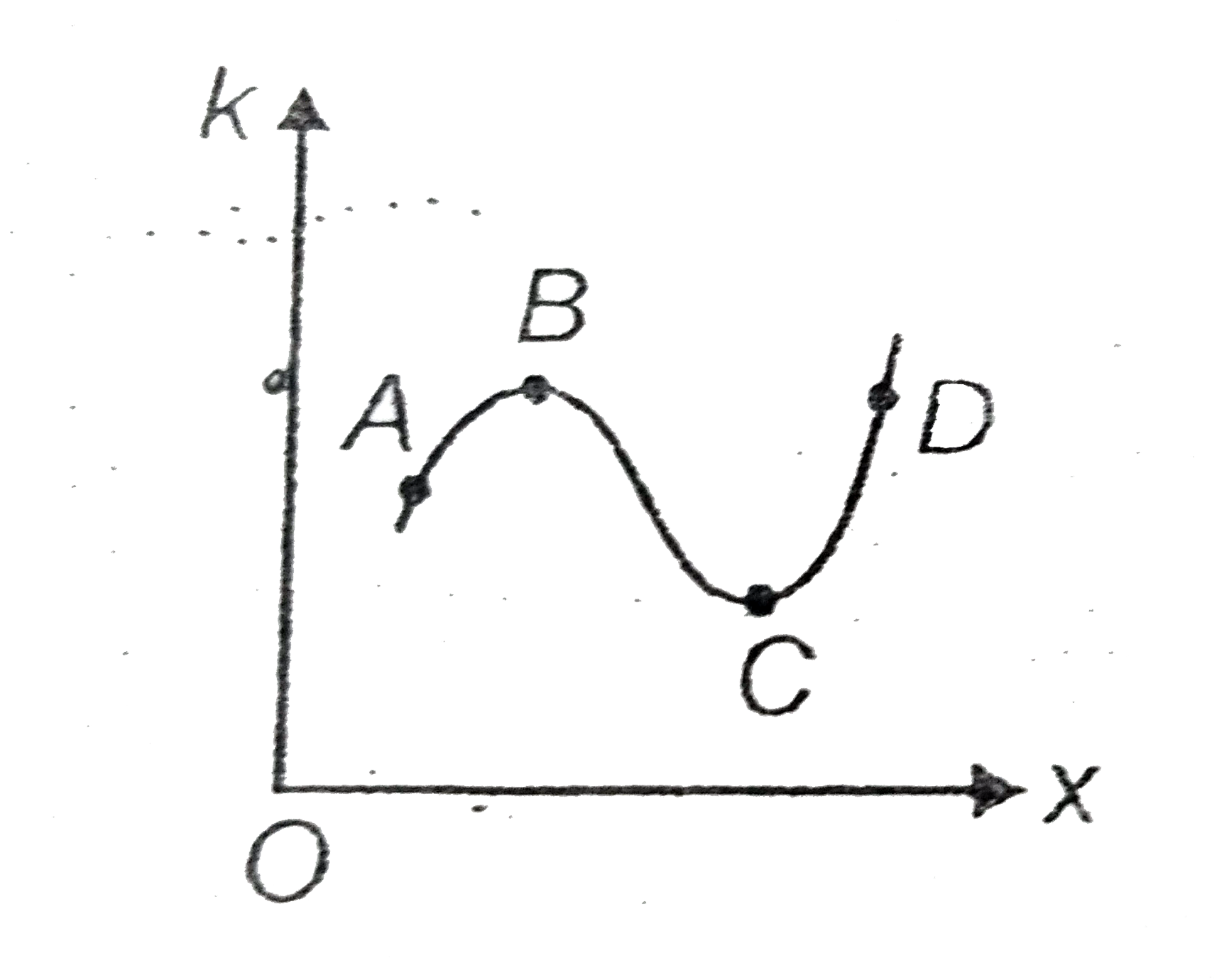
View SolutionA particle is moving in a circular path of radius r under the action of a force F. If at an instant velocity of particle is v, and speed of particle is increasing, then
View Solution
