A particle is moving along x-axis under the action of a force F, which varies with its position (x)asF∝1√x.Find the variation of power due to this force with x.
F∝x−1/4
⇒a∝x−1/4
⇒a=kx−1/4 (where k is a proportionality constant)
a=dvdt=dxdtdvdx=kx−1/4
vdvdx=kx−1/4dx
∈vdv=k∫×−1/4dx
∫vdv=k∫x−1/4dx.
v22=kx3/43/4
v2∝x3/4
v∝x3/8
∴P=Fv
P∝v3/8x1/4
P∝x1/8
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:IILUSTRATION
Explore 2 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:TRY YOURSELF
Explore 95 Videos
- WAVESBook:AAKASH INSTITUTE ENGLISHChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
A particle is moving along x-axis under the action of force, F which varies with its position as F∝14√x. Find the variation of power due to this fore with x.
View SolutionA particle is moving along x-axis under the action of a force, F which varies with its position (x) as F∝x−1/4. The variation of power due to this force with x is
View SolutionFor a particle moving under the action of a variable force, kinetic energy (k) varsus position (x) graph is given, then
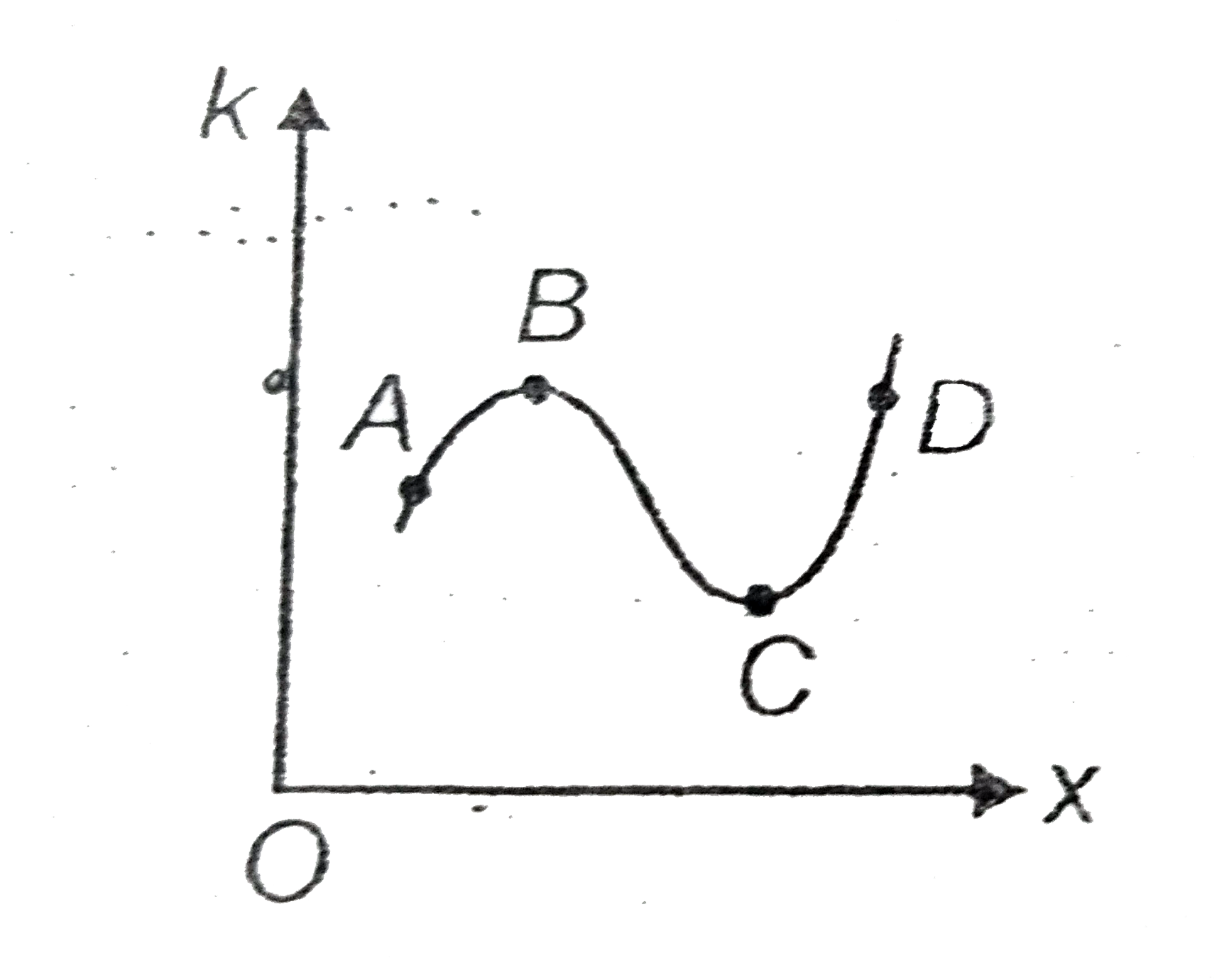
View SolutionA particle starts moving from rest along y axis and a variable force F acts on it such that F∞y−15 (y>0). The variation of power P of this force with y is given as
View SolutionFor a particle moving under the action of a variable force, kinetic energy (k) versus position (x) graph is given, then

View SolutionA particle is moving along x-axis. Its velocity v with x co-ordinate is varying as v=√x. Then
View SolutionA particle of mass m moves from rest under the action of a constant force F which acts for two seconds. The maximum power attained is
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View SolutionUnder the action of a force F = Cx, the position of a body changes from 0 to x. The work done is
View Solution