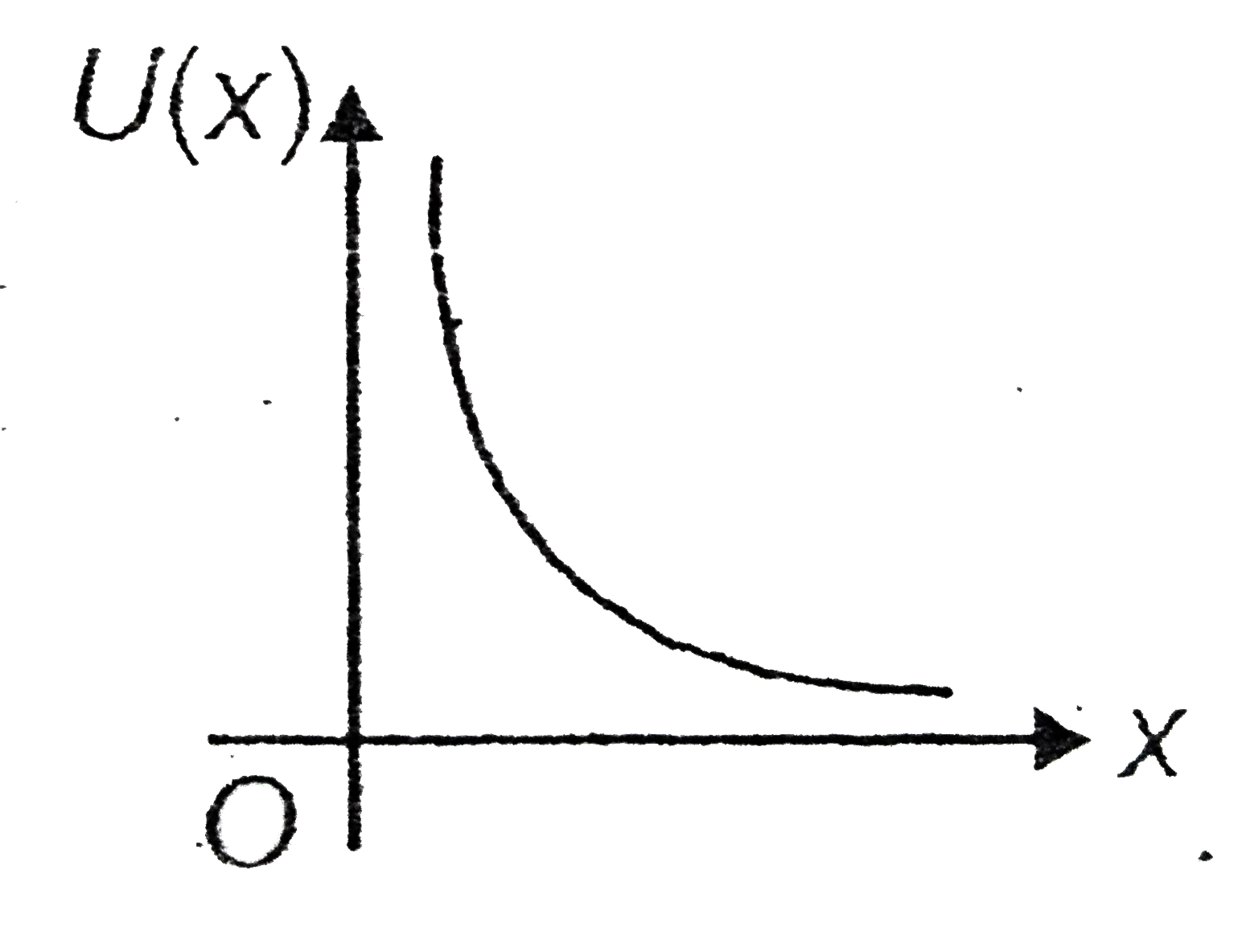
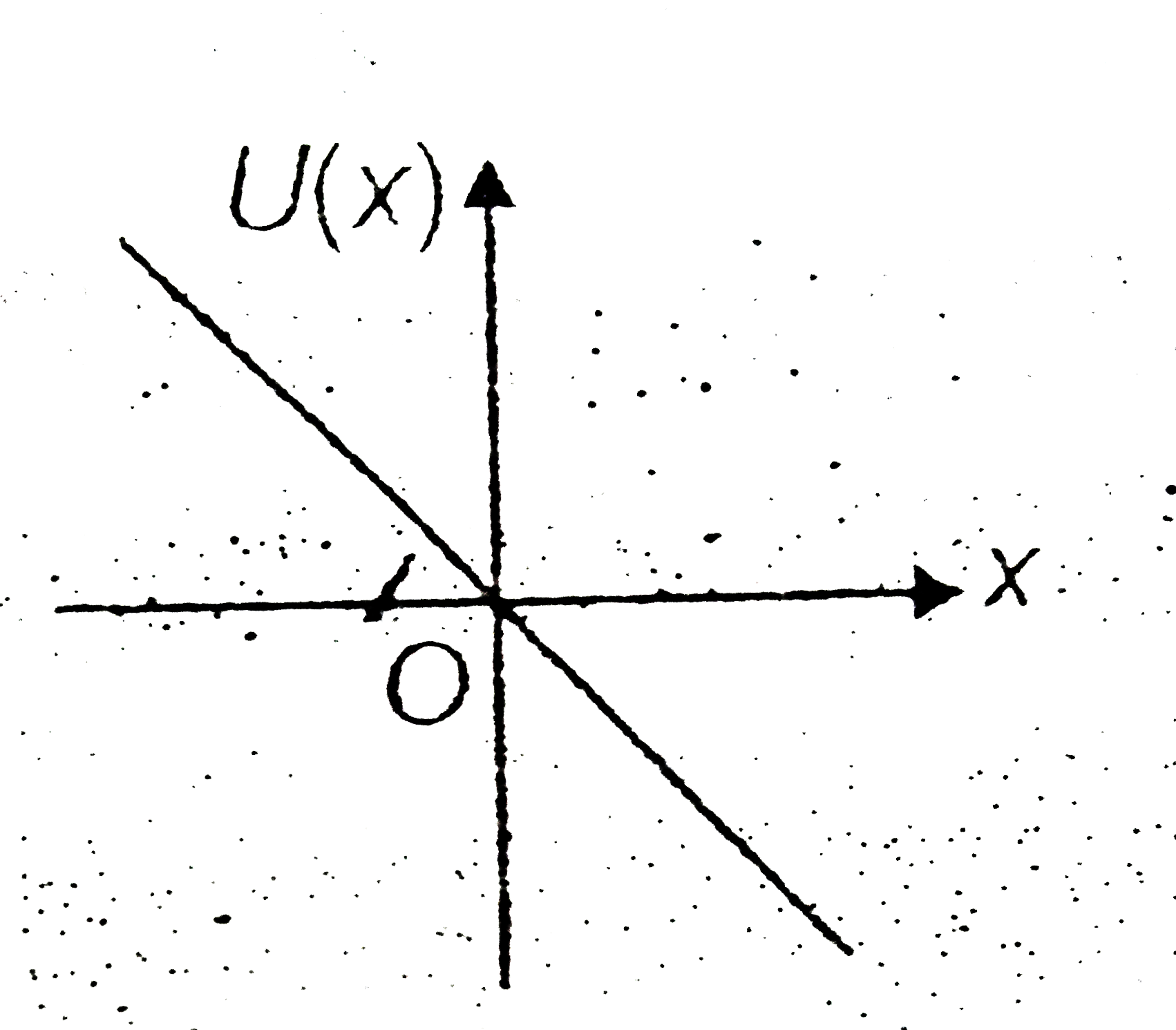
A particle is placed at the origin and a force F=kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) versus x will be (where, (U) is the potintial enetgy function). (a)  , (b)
, (b)  , (c) <img alt=) , (d)
, (d) 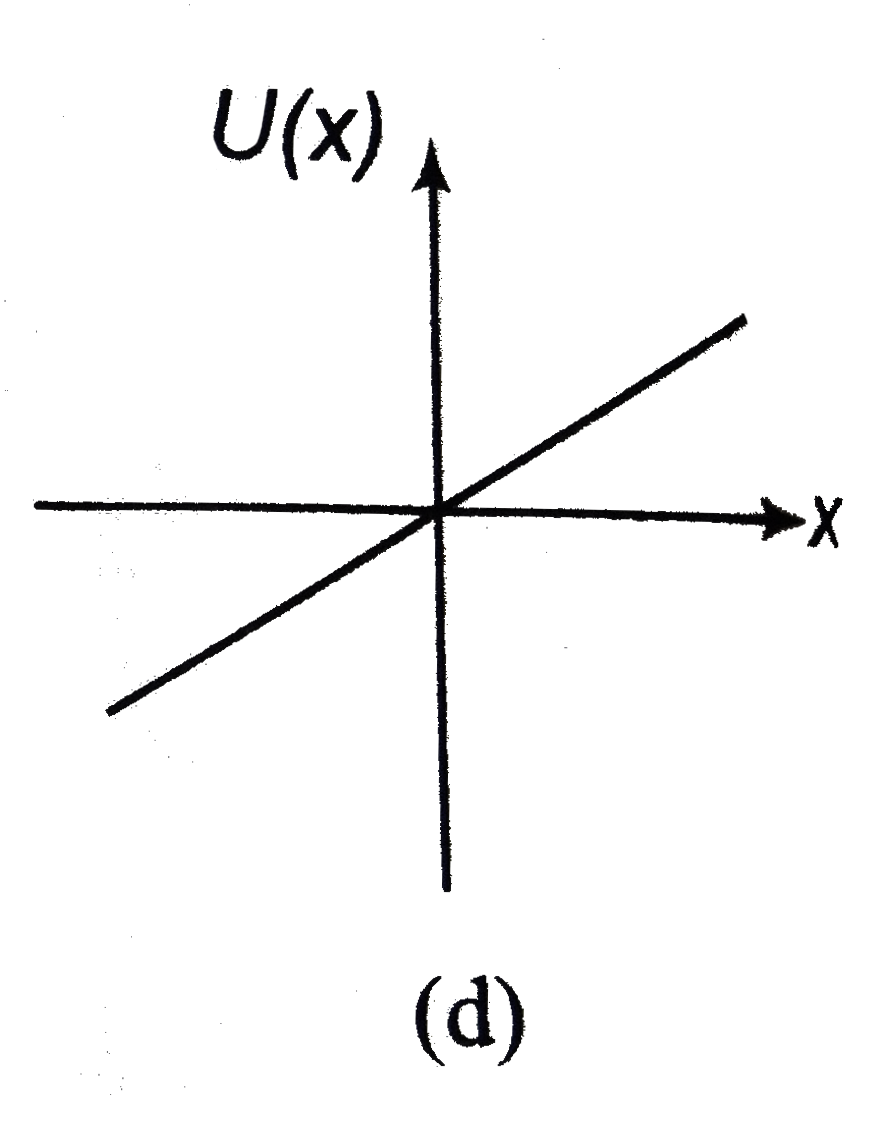 .
.


The correct Answer is:B
Step by step video & image solution for A particle is placed at the origin and a force F=kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) versus x will be (where, (U) is the potintial enetgy function). (a) , (b) , (d) . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)
45 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-C (OBJECTIVE TYPE QUESTIONS) (MORE THAN ONE OPTIONS ARE CORRECT)
16 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF
95 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
View SolutionA particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
View SolutionOn a particle placed at origin a variable force F=−ax(where a is a positive constant) is applied. If U(0)=0, the graph between potential energy of particle U(x) and x is best represented by:-
View SolutionA particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with the distance x of the particle from the origin an F(x)=−kx+ax3. Here, k and a are positive constants. For x(≥0, the functional form of the potential energy (u) U of the U (x) the particle is.
(a)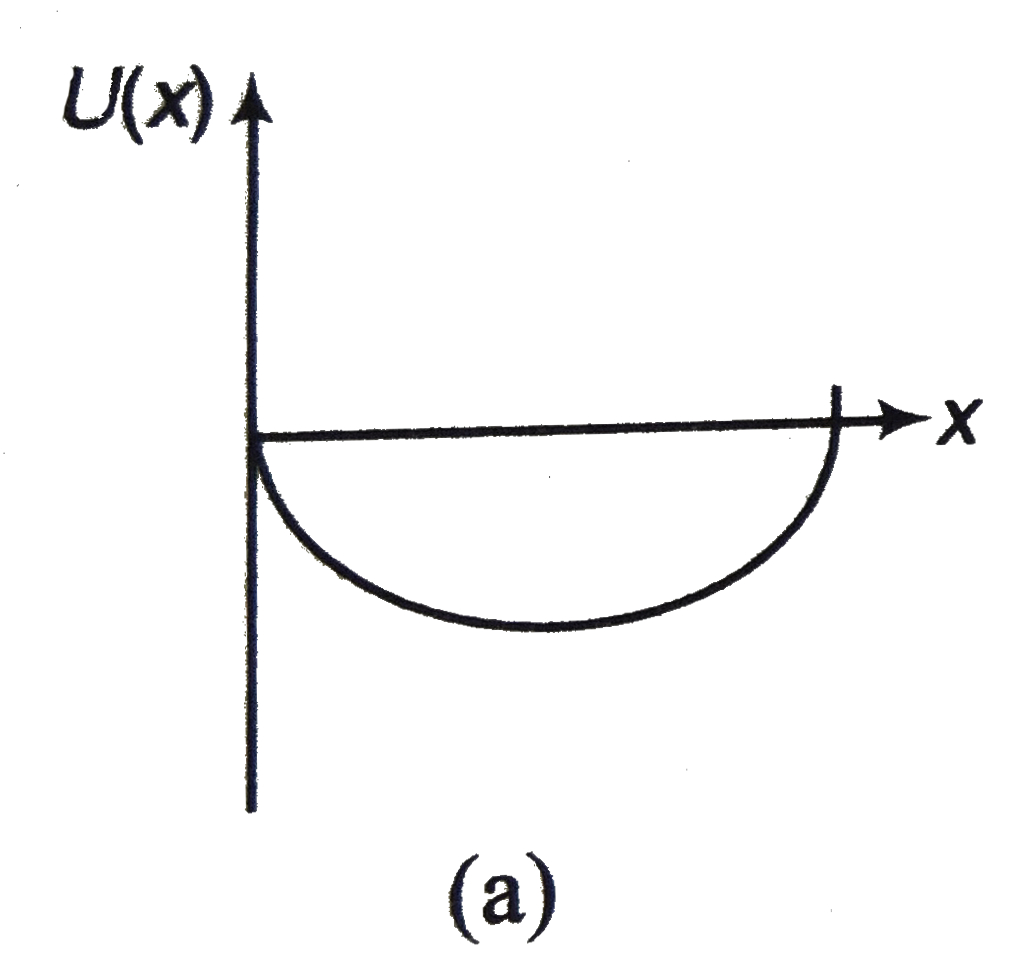 , (b)
, (b) 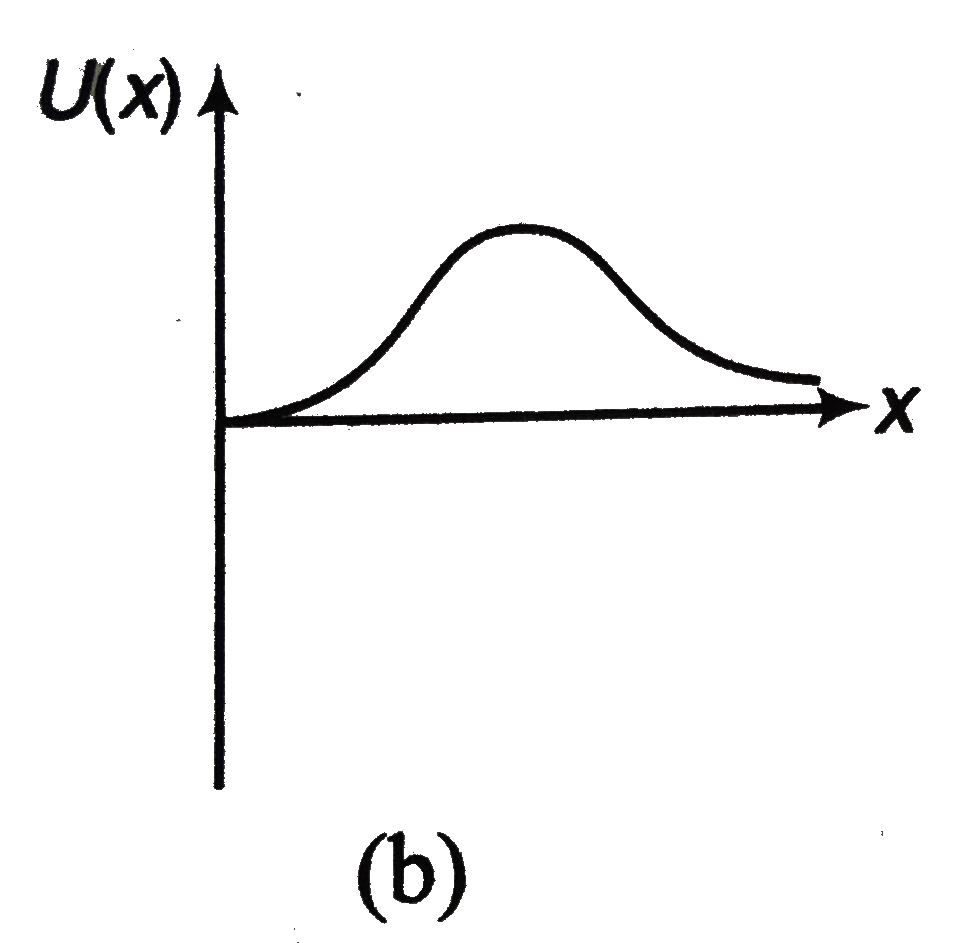 , (c)
, (c) 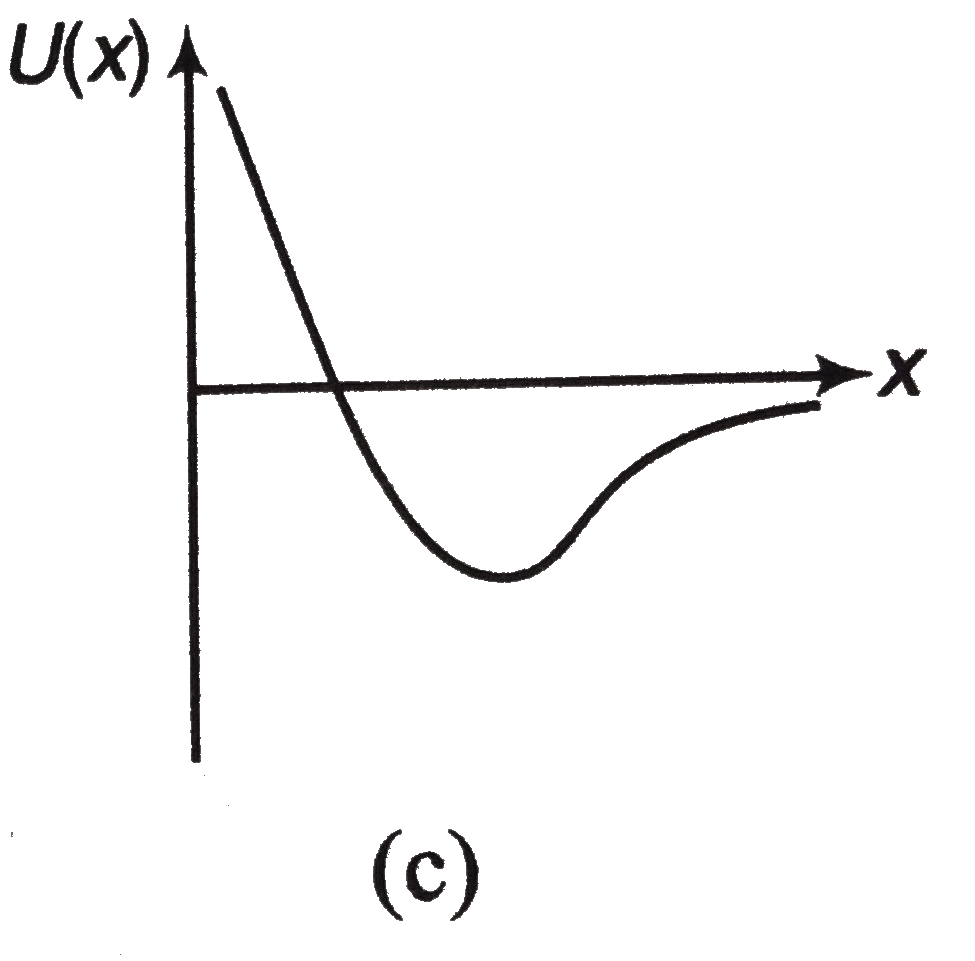 , (d)
, (d) 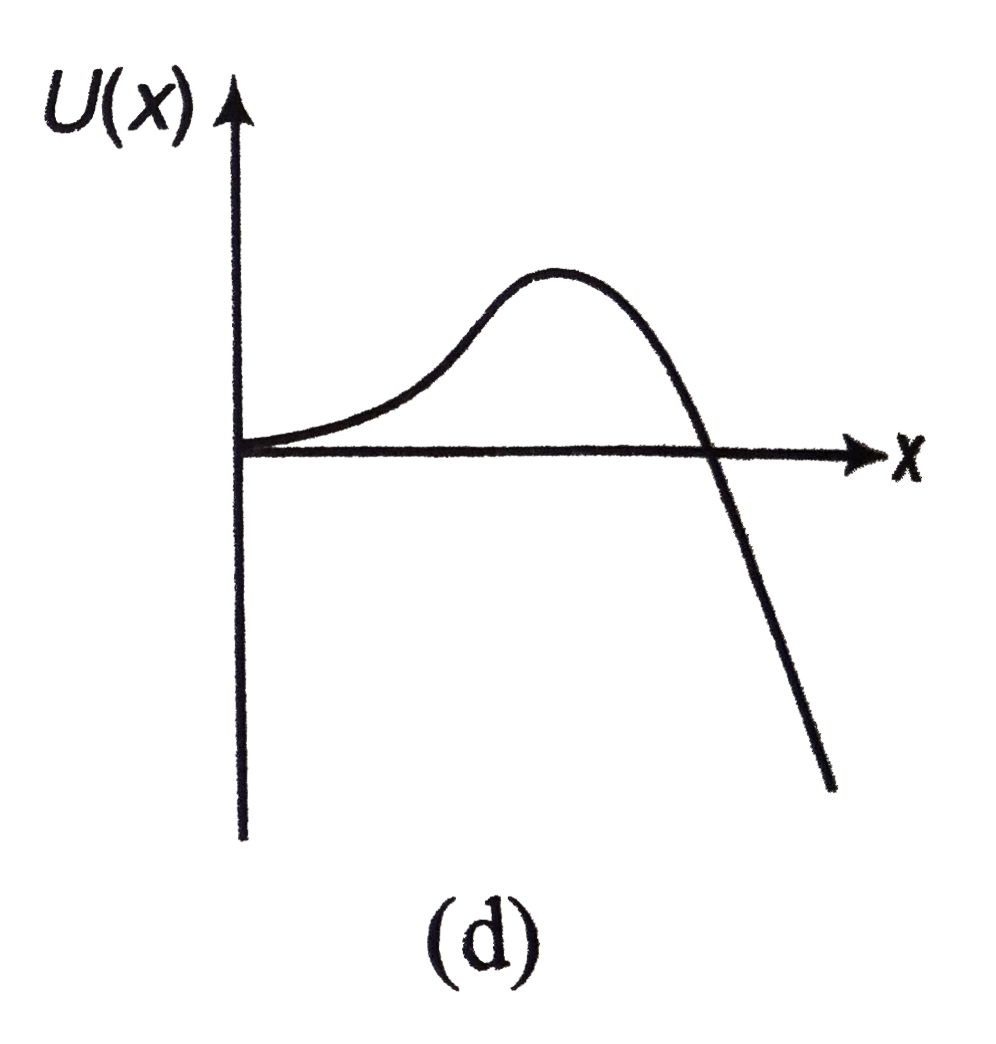 .
.
View SolutionA particle is moving along the x-axis and force acting on it is given by F=F0sinωxN, where ω is a constant. The work done by the force from x=0 to x=2 will be
View SolutionThe potential energy U for a force field →F is such that U=−kxy where K is a constant . Then
View SolutionA particle moving along the X-axis executes simple harmonic motion, then the force acting on it is given by
where, A and K are positive constants.
View SolutionThe potential energy of configuration changes in x and y directions as U=kxy, where k is a positive constant. Find the force acting on the particle of the system as the function of x and y.
View SolutionA particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants., the correct variation of potential energy function U(x) is best represented by.
View SolutionA particle is projected from origin x-axis with velocity V0 such that it suffers retardation of magnitude given by Kx3 (where k is a positive constant).The stopping distance of particle is
View Solution
