A car of mass m has an engine which can deliver power P. The minimum time in which car can be accelerated from rest to a speed v is :-
mv22P
Pmv2
2Pmv2
mv22P
The correct Answer is:A
To solve the problem of finding the minimum time in which a car can be accelerated from rest to a speed v given that the car has a mass m and an engine that can deliver power P, we can follow these steps:
1. Understand the Definition of Power:
Power (P) is defined as the rate at which work is done or energy is transferred. Mathematically, it can be expressed as:
P=Wt
where W is the work done and t is the time taken.
2. Express Work Done in Terms of Power:
Rearranging the formula for power gives us:
W=P⋅t
This equation will help us relate work done to time.
3. Use the Work-Energy Theorem:
According to the work-energy theorem, the work done on an object is equal to its change in kinetic energy. The kinetic energy (KE) of an object is given by:
KE=12mv2
Since the car starts from rest (initial velocity u=0), the change in kinetic energy when it reaches speed v is:
ΔKE=KEfinal−KEinitial=12mv2−0=12mv2
4. Set Work Done Equal to Change in Kinetic Energy:
From the work-energy theorem, we can equate the work done to the change in kinetic energy:
P⋅t=12mv2
5. Solve for Time t:
Rearranging the equation to solve for t:
t=12mv2P
Simplifying gives:
t=mv22P
Final Answer:
Thus, the minimum time in which the car can be accelerated from rest to a speed v is:
t=mv22P
Power (P) is defined as the rate at which work is done or energy is transferred. Mathematically, it can be expressed as:
P=Wt
where W is the work done and t is the time taken.
Rearranging the formula for power gives us:
W=P⋅t
This equation will help us relate work done to time.
According to the work-energy theorem, the work done on an object is equal to its change in kinetic energy. The kinetic energy (KE) of an object is given by:
KE=12mv2
Since the car starts from rest (initial velocity u=0), the change in kinetic energy when it reaches speed v is:
ΔKE=KEfinal−KEinitial=12mv2−0=12mv2
From the work-energy theorem, we can equate the work done to the change in kinetic energy:
P⋅t=12mv2
Rearranging the equation to solve for t:
t=12mv2P
Simplifying gives:
t=mv22P
Thus, the minimum time in which the car can be accelerated from rest to a speed v is:
t=mv22P
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)45videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-C (OBJECTIVE TYPE QUESTIONS) (MORE THAN ONE OPTIONS ARE CORRECT)16videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF95videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))12videos
WAVES
Similar Questions
A car of mass m has an engine which can deliver constant power P.the maximum speed that the car can attain in t seconds in
View SolutionA car is moving up the plane. Angle of inclination is θ and coeffcient of friction is μ
(a)What is the condition in which car can be acceleration?
If this condition is satisfied then find (b) maximum acceleration of the car.
(c) minimum retardation of the car.
(d) maximum retardation of the car.View Solution
Knowledge Check
- Question 1 - Select One
A car can be stopped within a distance of s when its speed is v. What is the minimum distance within which the car can be stopped during the same time when its speed is nv ?
AnsBs/nCn2sDs/n2 - Question 2 - Select One
The maximum acceleration that can be produced by the engine of a vehicle is 5ms−2 and the maximum retardation is brake can produce is 10ms−2. Then the minimum time during which it can cover a distance of 60 m is
A6 sB5 sC36 sD24 s.
On a horizontal rough road , value of coefficient of friction μ=0.4.Find the minimum time in which a distance of 400m can be covered. The car start from rest and finally comes to rest.
View SolutionA car of mass m is initially at rest on the boat of mass M tied to the wall of dock through a massless, inextensible string. The car accelerates from rest to velocity v0 in times to. At t=t0 the car applies brake and comes to rest relative to the boat in negligible time. Neglect friction between the boat and water: the time 't' at which boat will strike the wall is
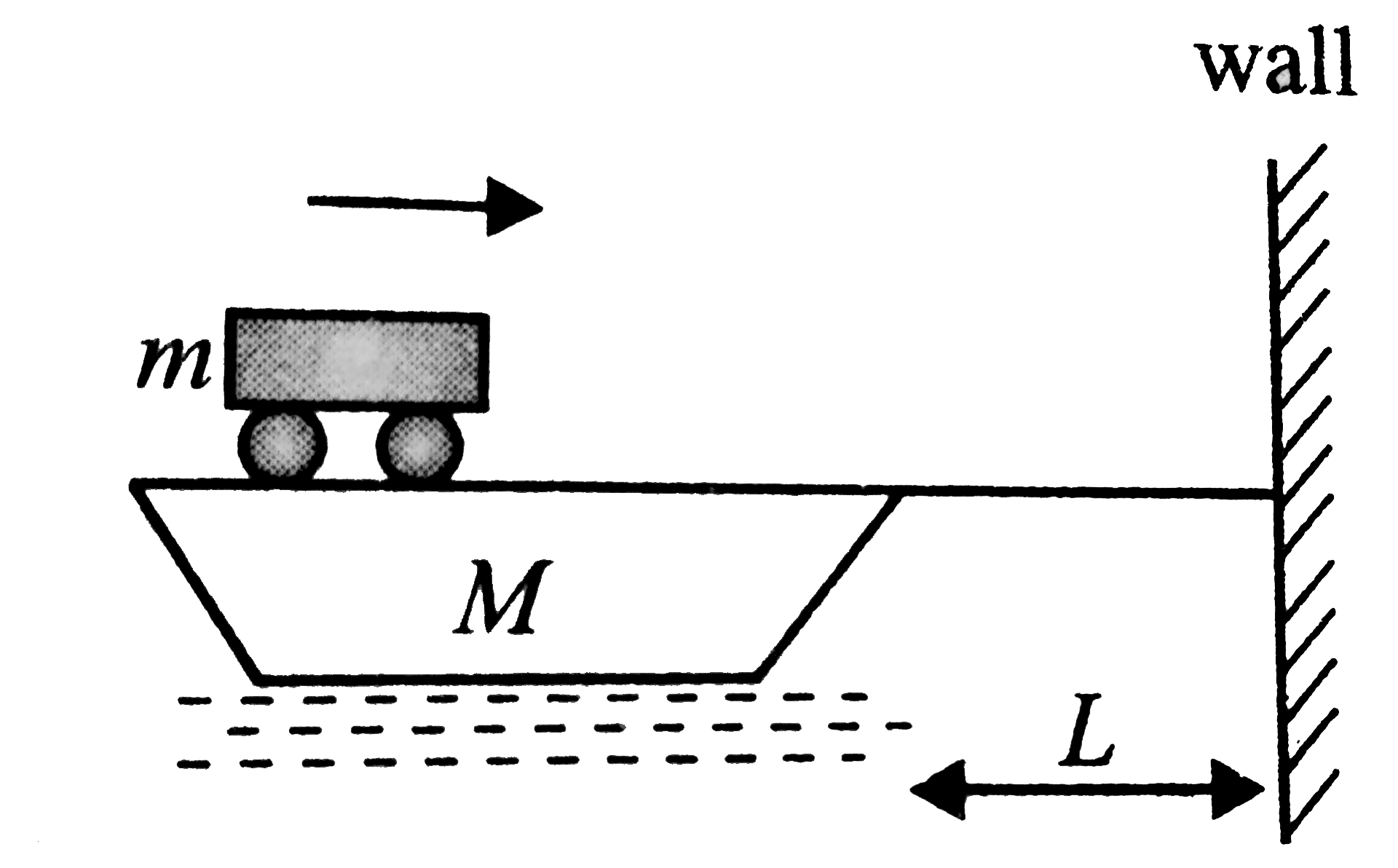 View Solution
View SolutionWhat is the power of an engine which can lift 600 kg of water per minute from 20 m deep well?
View SolutionA self-propelled vehicle of mass m, whose engine delivers a constant power P, has an acceleration a=(P/mv). (Assume that there is no friction). In order to increase its velocity from v1 to v2, the distan~e it has to travel will be:
View SolutionIn a car race, car A takes time t less than car B and passes the finishing point with a velocity of 12m/s more than the velocity with which car B passes the finishing point. Assume that the cars A and B start from rest and travel with constant acceleration of 9m/s2and 4m/s2 , respectively. If vA and vB be the velocities of cars A and B, respectively, then
View SolutionA body of mass 2 kg is driven by an engine delivering a constant power of 1 J /s. The body starts from rest and moves in a straight line. After 9 seconds, the body has moved a distance ( in m) ……….. .
View Solution
