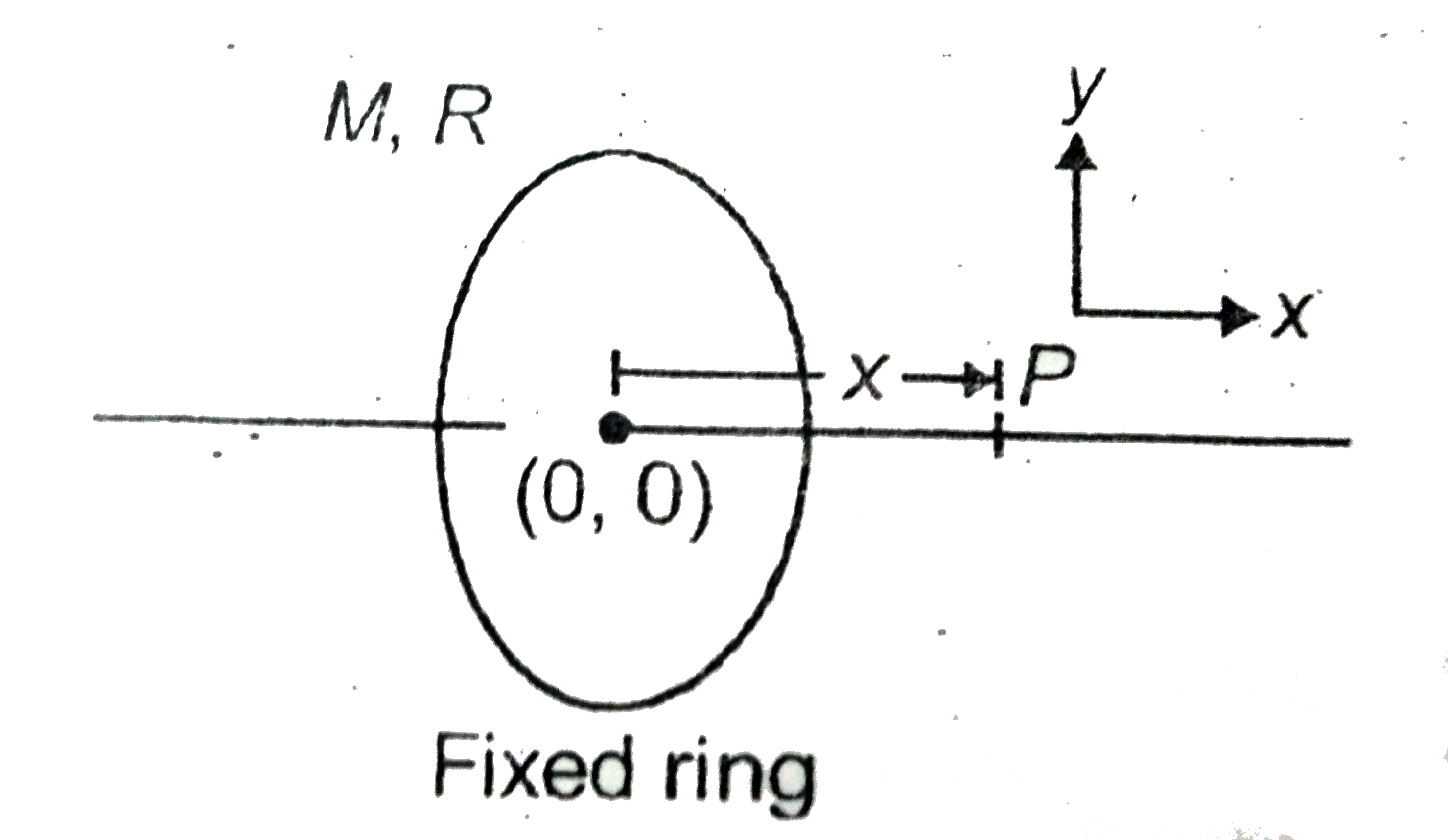
The gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
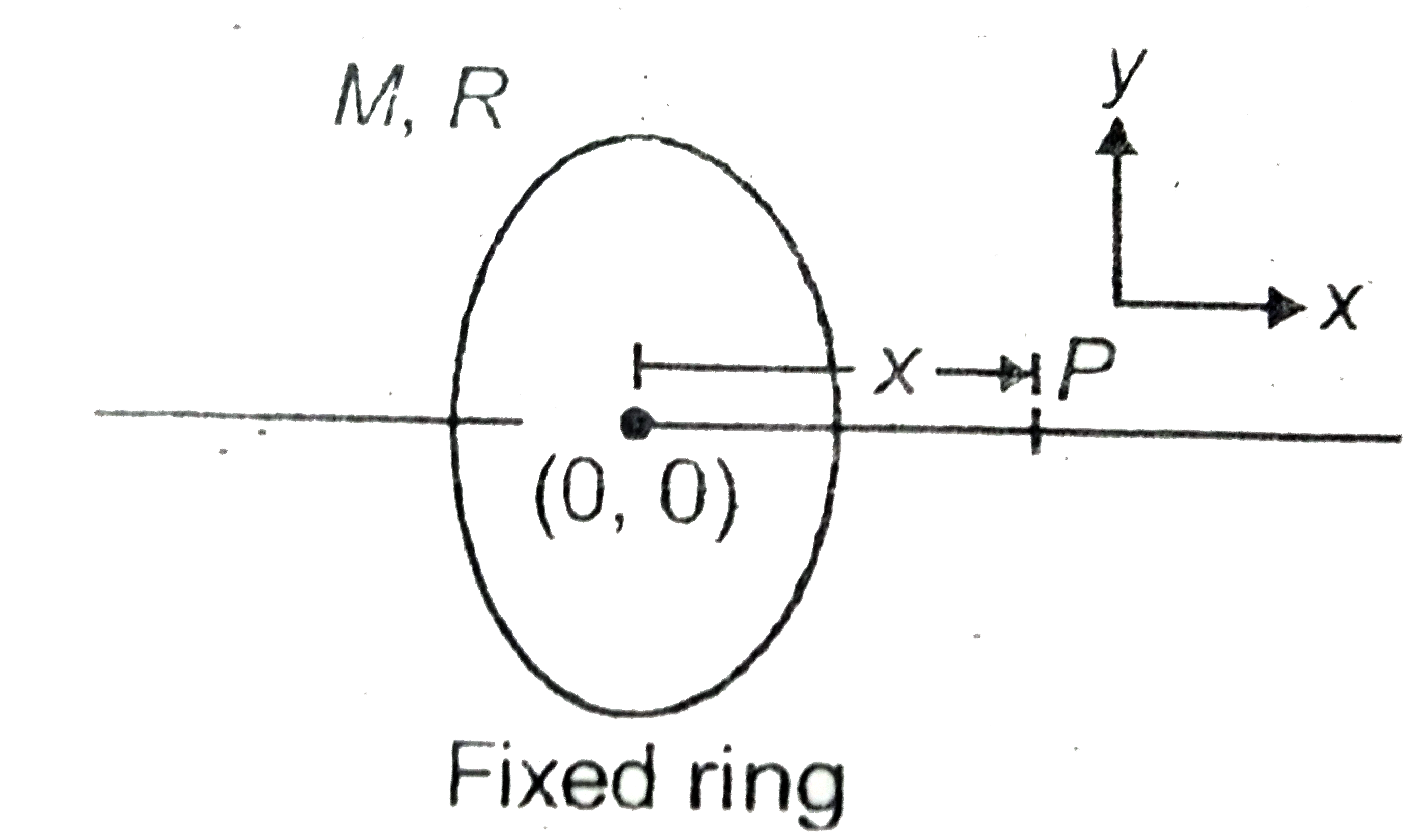
For a point near to the centre i.e., x lt lt R, the intensity of gravitational field E
E∝x
E∝x2x3/2
E∝x−3/2
E∝1x2
The correct Answer is:A
Step by step video & image solution for The gravitational force vec(F) upon an object of mass m placed in external gravitational field vec(E )_("ext") is given by vec(F)=m vec(E )_("ext"). Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction. For a point near to the centre i.e., x lt lt R, the intensity of gravitational field E by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -E (Assertion - Reason Type Questions)
14 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -F (Matrix - Match Type Questions)
8 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -C (Objective Type Questions (More than one option are correct))
12 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
The gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
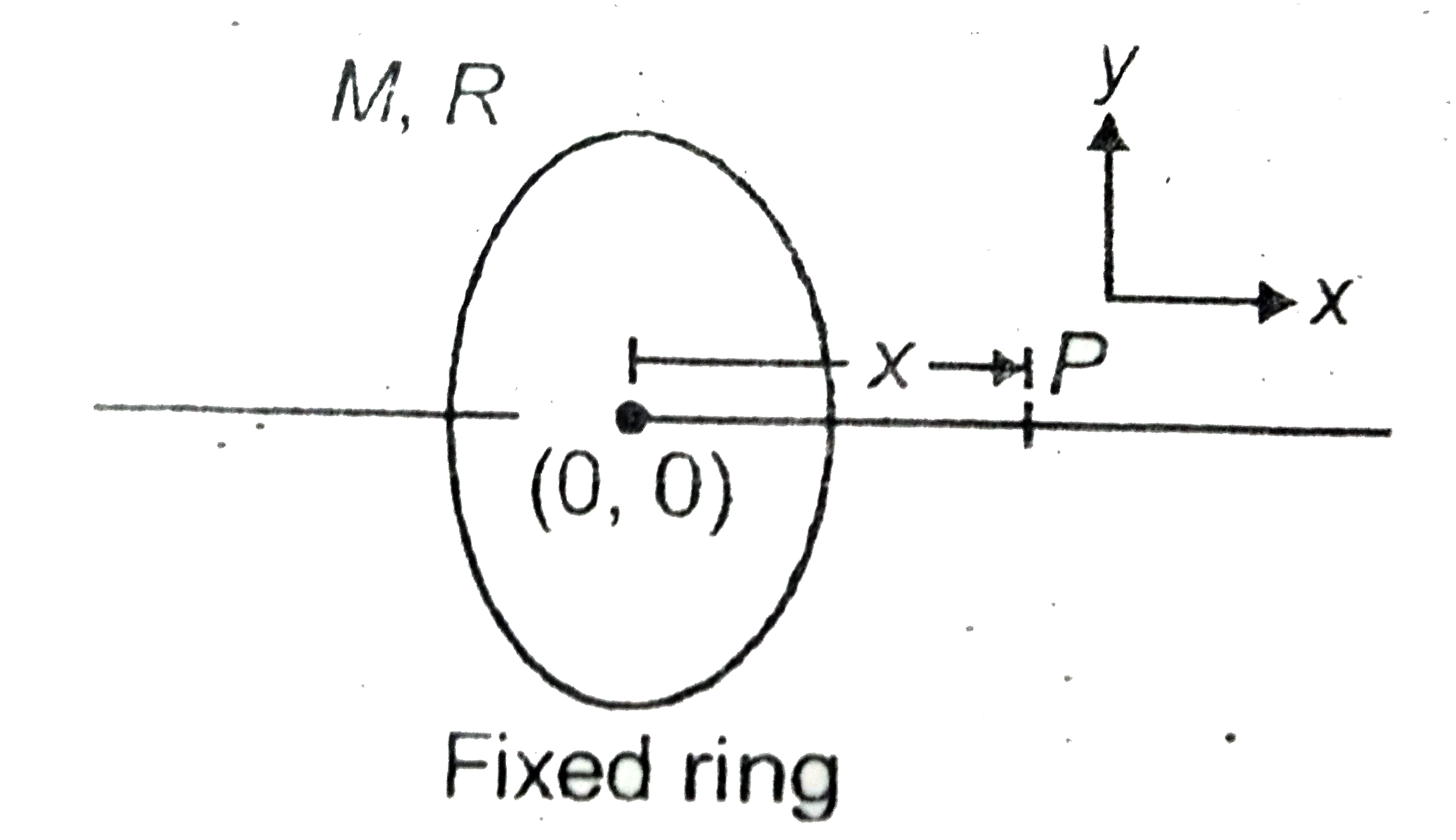
The gravitational field is zero at x equal to
View SolutionThe gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
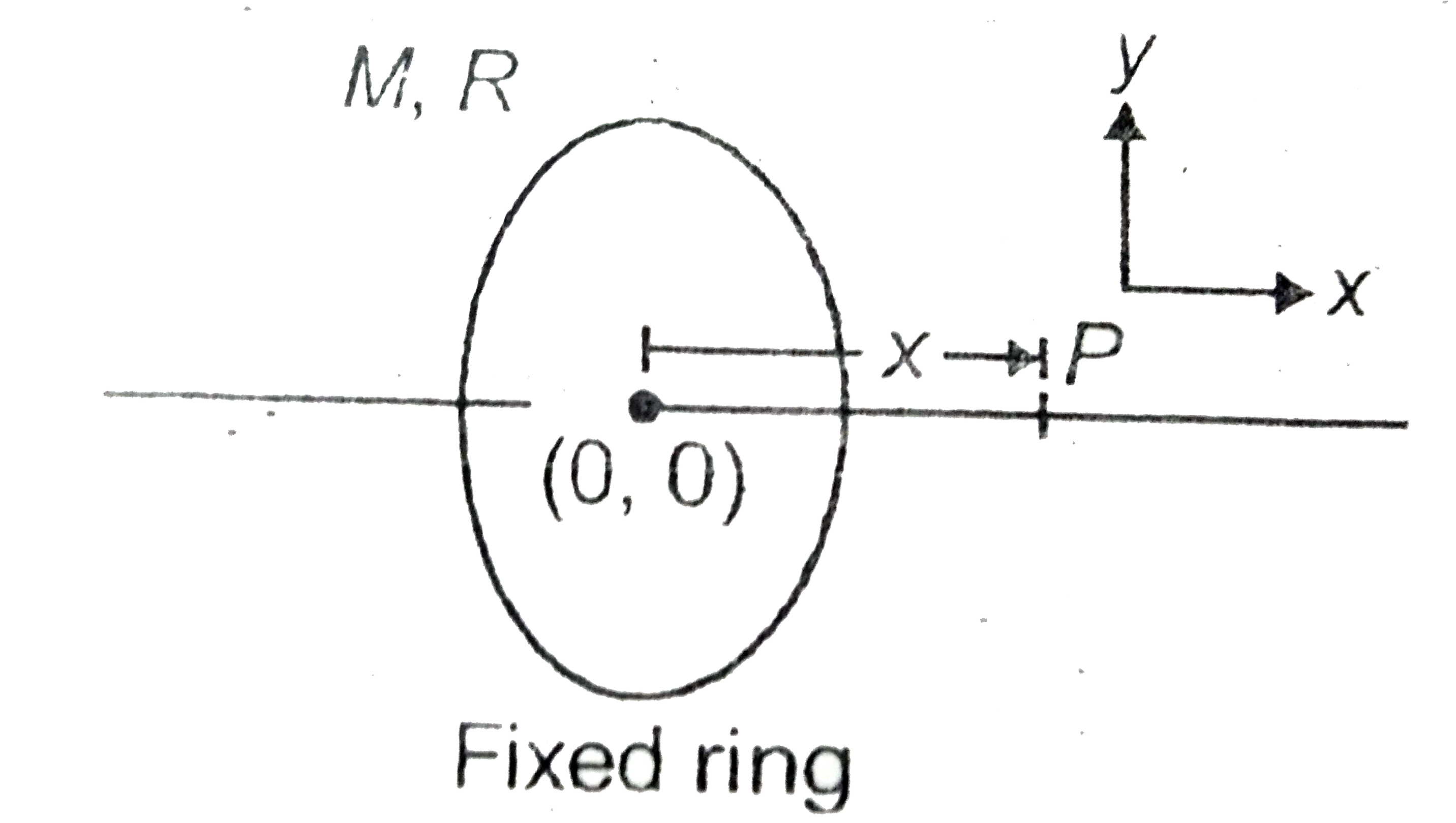
The value of maximum gravitational field intensity is
View Solution
Knowledge Check
A mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass m is
AGMm√2R2BGMm2R2CGMm2√2R2DGMm4R2
The gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
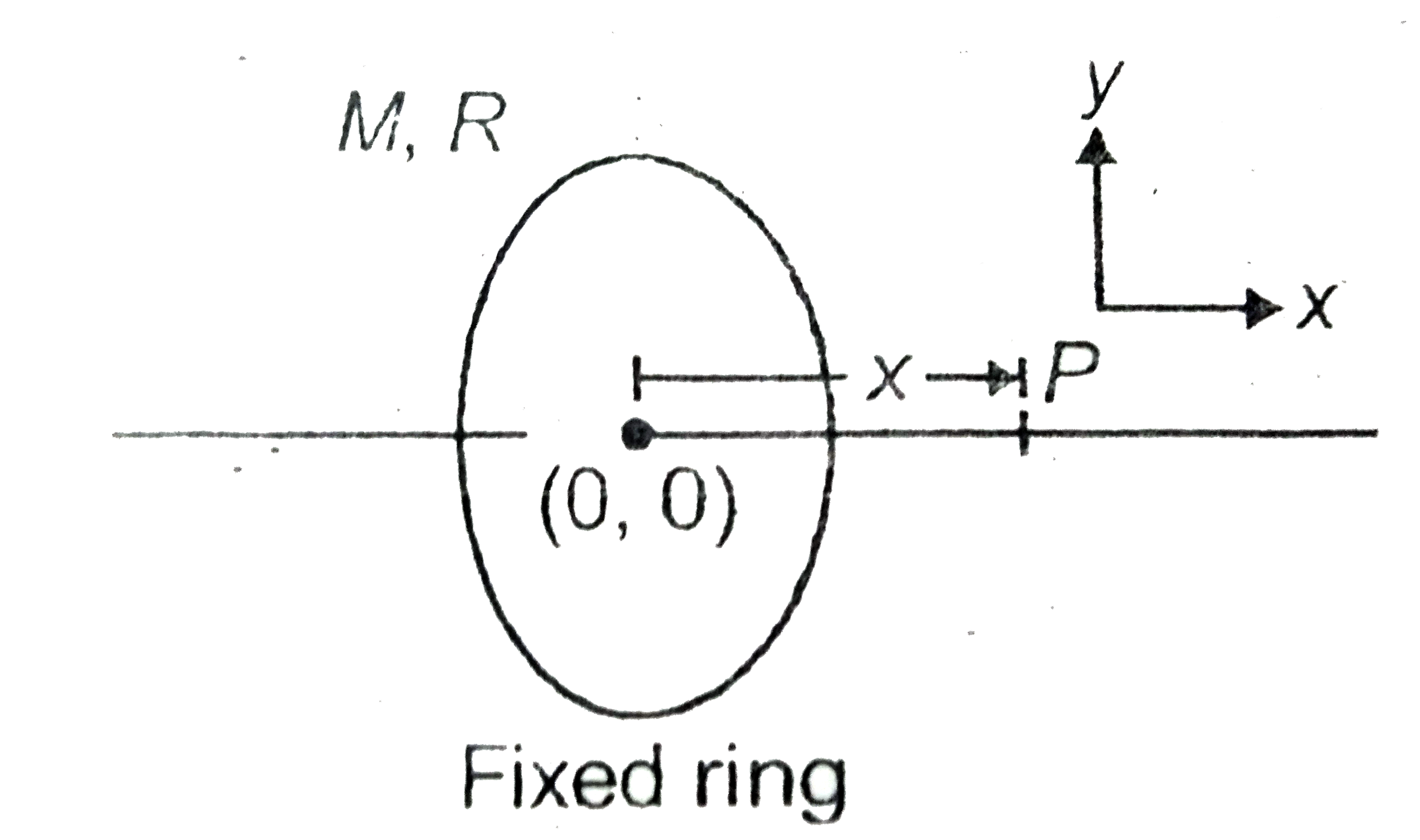
If the point mass m placed at the centre of ring and given a velocity v0 such that point mass escapes from the gravitational field of ring. Then v0 is
View SolutionThe gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
If the particle (mass m) is released from rest from a point distant x=R√3, then it will pass through the centre of ring with speed
View SolutionConsider a ring of mass m and radius r. Maximum gravitational intensity on the axis of the ring has value.
View SolutionFind the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
View SolutionA ring of mass m1 and radius R is fixed in space at some location. An external agent brings a point mass m2 from infinity to centre of the ring. Work done by the external agent will be
View SolutionThree identical point mass each of mass 1kg lie in the x-y plane at point (0,0), (0,0.2m) and (0.2m, 0). The net gravitational force on the mass at the origin is
View SolutionThree identical point mass each of mass 1kg lie in the x-y plane at point (0,0), (0,0.2m) and (0.2m, 0). The net gravitational force on the mass at the origin is
View Solution
