A load of 20 kg produces an extension of 1 mm in a wire 3 m in length and 1 mm in diameter.l Calculate Young's modulus of elesticity of wire.
3.25×1010Nm−2
7.48×1010Nm2
7.48×1010Nm−2
7.48×10−10Nm−2
The correct Answer is:C
To calculate Young's modulus of elasticity for the given wire, we will follow these steps:
Step 1: Identify the given values
- Load (mass) m=20kg
- Extension ΔL=1mm=1×10−3m
- Original length of the wire L=3m
- Diameter of the wire d=1mm=1×10−3m
Step 2: Calculate the force (F) applied on the wire
The force can be calculated using the formula:
F=m⋅g
where g (acceleration due to gravity) is approximately 9.81m/s2.
Substituting the values:
F=20kg⋅9.81m/s2=196.2N
Step 3: Calculate the cross-sectional area (A) of the wire
The area A can be calculated using the formula for the area of a circle:
A=πr2
First, we need to find the radius r:
r=d2=1×10−3m2=0.5×10−3m=0.0005m
Now substituting the radius into the area formula:
A=π(0.0005m)2=π(0.00000025m2)≈7.85×10−7m2
Step 4: Calculate the strain (ε)
Strain is defined as the change in length divided by the original length:
Strain(ϵ)=ΔLL=1×10−3m3m=13000≈3.33×10−4
Step 5: Calculate the stress (σ)
Stress is defined as force per unit area:
Stress(σ)=FA=196.2N7.85×10−7m2≈2.5×1011N/m2
Step 6: Calculate Young's modulus (E)
Young's modulus is defined as the ratio of stress to strain:
E=σϵ=2.5×1011N/m23.33×10−4≈7.5×1010N/m2
Final Answer
Thus, the Young's modulus of elasticity of the wire is approximately:
E≈7.5×1010N/m2
- Load (mass) m=20kg
- Extension ΔL=1mm=1×10−3m
- Original length of the wire L=3m
- Diameter of the wire d=1mm=1×10−3m
The force can be calculated using the formula:
F=m⋅g
where g (acceleration due to gravity) is approximately 9.81m/s2.
F=20kg⋅9.81m/s2=196.2N
The area A can be calculated using the formula for the area of a circle:
A=πr2
First, we need to find the radius r:
r=d2=1×10−3m2=0.5×10−3m=0.0005m
A=π(0.0005m)2=π(0.00000025m2)≈7.85×10−7m2
Strain is defined as the change in length divided by the original length:
Strain(ϵ)=ΔLL=1×10−3m3m=13000≈3.33×10−4
Stress is defined as force per unit area:
Stress(σ)=FA=196.2N7.85×10−7m2≈2.5×1011N/m2
Young's modulus is defined as the ratio of stress to strain:
E=σϵ=2.5×1011N/m23.33×10−4≈7.5×1010N/m2
Thus, the Young's modulus of elasticity of the wire is approximately:
E≈7.5×1010N/m2
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment (SECTION - B)
15 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment (SECTION - C)
2 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Try Yourself
32 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- Mock test 03BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - Mock test 03EXERCISE - EXAMPLE
44 Videos
Similar Questions
A load of 2 kg produces a certain extension in a wire of length 6m and diameter 1mm. What is the lateral contraction produced if σ=0.25 and Y=7.48×1010N/m2 ?
View SolutionA loud of 10 kg stretches a wire 5 m long und 1 mm diameter by 0.3 mm. Find Young.s modulus of the material of the wire and energy stored in the wire.
View SolutionWhat is the percentage increase in length of a wire of diameter 2.5 mm, stretched by a force of 100 kg wt ? Young's modulus of elasticity of wire =12.5×1011dyne/cm2.
View SolutionA wire of length 15m and diameter 4 mm elongates 0.3mm when stretched by weigth of 2.20kg. Calulate the Young's modulus of the material of the wire.
View SolutionThe area of cross - section of a wire is 1 mm2 and it length is 2 m. How much work will be done to increase its length by 0.1 mm ? The Young.s modulus of elaticity for the material of the wire is 2×1011 Nm−2.
View SolutionThe adjacent graph shows the estension (Δl) of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is 10−6m2, calculate the Young's modulus of the material of the wire.
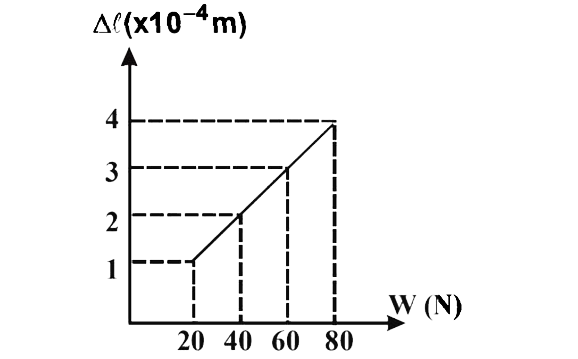
View Solution_S01_065_Q01.png)
The graph shows the extension of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm2, then the young's modulus of the material of the wire is
(a). 2×1011Nm−2
(b). 2×1010Nm−2
(c). 12×1011Nm−2
(d). none of these
View SolutionA wire 3m long and diameter 0.3 mm is stretched by a load of 2kg. If the elongation is 2mm, find the Young.s modulus of the material of the wire and the potential energy stored in the wire.
View SolutionA load of 4kg is suspended from a ceiling through a steel wire of length 20m and radius 2mm. It is found that the length of the wire increases by 0.031mm, as equilibrium is achieved. If g=3.1×πms(−2), the value of young's modulus of the material of the wire (in Nm−2) is
View SolutionA steel wire of length 600cm and diameter 1.2 mm is stretched through 4 mm by a load. Calculate the work done. Young's modulus of steel =2×1011Nm−2.
View Solution